Calcul l’effort tranchant et le moment
Comprendre le calcul l’effort tranchant et le moment :
Vous êtes ingénieur en structure et vous devez analyser une poutre simplement appuyée. Cette poutre supporte plusieurs charges réparties et concentrées.
Données
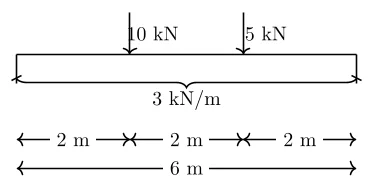
- Longueur de la poutre, : 6 m
- Une charge uniformément répartie de 3 kN/m sur toute la longueur de la poutre.
- Une charge ponctuelle de 10 kN appliquée à 2 m du support gauche.
- Une charge ponctuelle de 5 kN appliquée à 4 m du support gauche.
En savoir plus sur le Tracé d’Effort Tranchant et du Moment Fléchissant
Questions
- Réaction aux Appuis : Calculez les réactions aux appuis de la poutre.
- Effort Tranchant :
- Tracez le diagramme de l’effort tranchant pour la poutre.
- Calculez l’effort tranchant à 1 m, 3 m et 5 m de l’extrémité gauche.
- Moment Fléchissant :
- Tracez le diagramme du moment fléchissant pour la poutre.
- Calculez le moment fléchissant à 1 m, 3 m et 5 m de l’extrémité gauche.
- Point de Moment Maximal : Déterminez la position et la valeur du moment maximal dans la poutre.
Indications
- Considérez la poutre comme étant en équilibre statique.
- Utilisez les principes de la mécanique des milieux continus pour résoudre l’exercice.
- N’oubliez pas que l’effort tranchant change aux points où il y a des charges appliquées.
Correction : Calcul l’effort tranchant et moment
1. Réaction aux Appuis
Pour une poutre simplement appuyée, les réactions aux appuis sont calculées en utilisant l’équilibre statique.
- Équilibre Vertical :
\begin{equation*}
\sum F_y = 0
\end{equation*} - Équilibre de Moment :
\begin{equation*}
\sum M = 0
\end{equation*}
Soient \( R_A \) et \( R_B \) les réactions aux appuis gauche et droit, respectivement.
- Charge totale due à la distribution uniforme :
\begin{equation*}
3 \, \text{kN/m} \times 6 \, \text{m} = 18 \, \text{kN}.
\end{equation*} - La force résultante de la charge distribuée agit au centre de la poutre, soit à 3 m de chaque appui.
- Application des équations d’équilibre :
\begin{align*}
R_A + R_B &= 18 \, \text{kN} + 10 \, \text{kN} + 5 \, \text{kN} \\
R_A + R_B &= 33 \, \text{kN}
\end{align*}
Pour le moment (en prenant le moment autour de A) :
\(R_B \times 6 \, \text{m} = 18 \, \text{kN} \times 3 \, \text{m} + 10 \, \text{kN} \times 2 \, \text{m} + 5 \, \text{kN} \times 4 \, \text{m}\)
\begin{align*} R_B &= \frac{54 + 20 + 20}{6} \, \text{kN} \\
R_B &= 15.67 \, \text{kN} \\
R_A &= 33 – 15.67 = 17.33 \, \text{kN}
\end{align*}
2. Effort Tranchant \(V(x)\)
- 0 – 2 m :
\(V(x)\) commence à 17.33 kN à l’appui A.
À 2 m, \(V(x) = 17.33 – 3 \times 2 = 11.33 \, \text{kN}\).
- À 2 m (charge ponctuelle) :
\(V(x)\) chute de 10 kN à \(1.33 \, \text{kN}\).
- 2 – 4 m :
\(V(x)\) continue de diminuer en raison de la charge distribuée.
Juste avant 4 m, \(V(x) = 1.33 – 3 \times 2 = -4.67 \, \text{kN}\).
- À 4 m (charge ponctuelle) :
\(V(x)\) chute de 5 kN à \(-9.67 \, \text{kN}\).
- 4 – 6 m :
À l’appui B, \(V(x)\) est de -15.67 kN, en accord avec \(R_B\).
3. Moment Fléchissant \(M(x)\)
- 0 – 2 m :
Le moment augmente linéairement puis de manière quadratique à cause de la charge distribuée.
À 1 m :
\(M(1) = 17.33 \times 1 – 3 \times \frac{1}{2} \times 1^2 = 15.83 \, \text{kNm}\).
- 2 – 4 m :
Le moment continue d’augmenter, atteignant un maximum où \(V(x) = 0\).
Trouvons où \(V(x) = 0\) entre 2 m et 4 m :
Équation de l’effort tranchant dans cette section : \(V(x) = 1.33 – 3 \times (x – 2)\).
Trouver \(x\) tel que \(V(x) = 0\) :
\begin{align*}
0 &= 1.33 – 3 \times (x – 2) \\
3x – 6 &= 1.33 \\
x &\approx 2.44 \, \text{m}
\end{align*}
- Calcul du moment à \(x = 2.44 \, \text{m}\) :
\( M(2.44) = 17.33 \times 2.44 – 3 \times \frac{2.44^2}{2} – 10 \times (2.44 – 2) \)
\( M(2.44) \approx 19.22 \, \text{kNm} \quad \text{(valeur approximative)} \) - 4 – 6 m :
À 5 m :
\( M(5) = 15.67 \times (6 – 5) – 3 \times \frac{1}{2} \times 1^2 = 14.17 \, \text{kNm} \).
4. Point de Moment Maximal
Le moment maximal se produit à environ \( x = 2.44 \, \text{m} \) de l’appui gauche, avec une valeur d’environ 19.22 kNm.
Diagramme de l’effort tranchant et du moment fléchissant
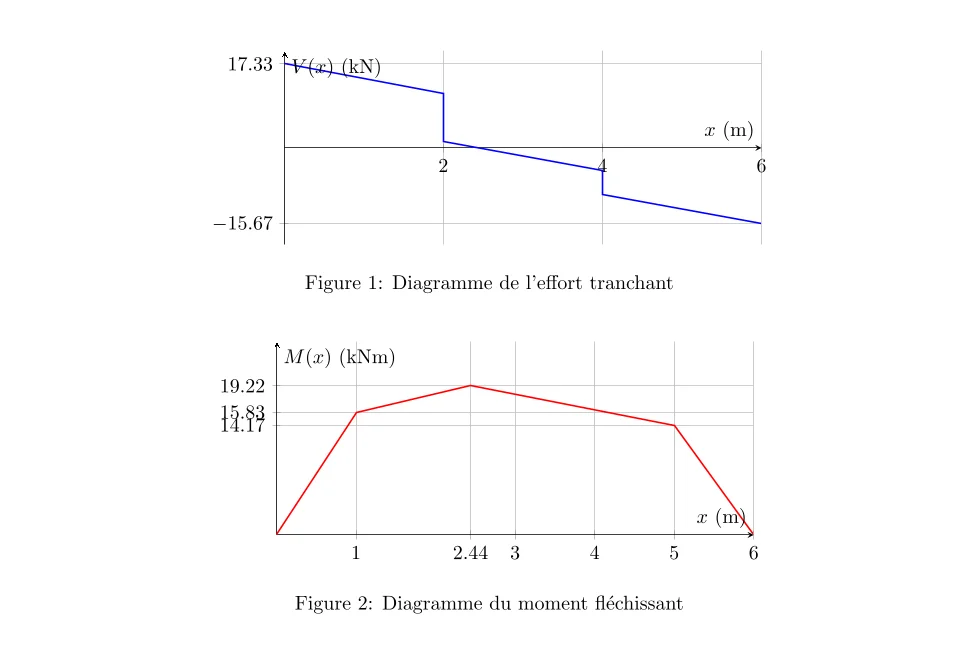
D’autres exercices de résistance des matériaux :




J’aime bien ce gens d’exercice
Bonjour,
Je suis en BUT GCCD 1ère année et j’ai du mal avec mes exercices de mécanique des structures, pour déterminer Vy ainsi que Mz à toute distance sur la poutre il nous est demandé de les déterminer en fonction de « x », je n’y arrive pas.
On arrive en fin de semestre et je n’ai plus TD mais les partiels arrivent à grand pas, serait-il possible d’en discuter par mail ?
Merci.
Cordialement Aurélien B.
Bonjour, vous pouvez nous écrire directement sur Contact@etudiantgeniecivil.com, Nous serons ravis de vous aider!!!