Contrainte de Compression dans un Pilier

Comprendre le calcul de la Contrainte de Compression dans un Pilier

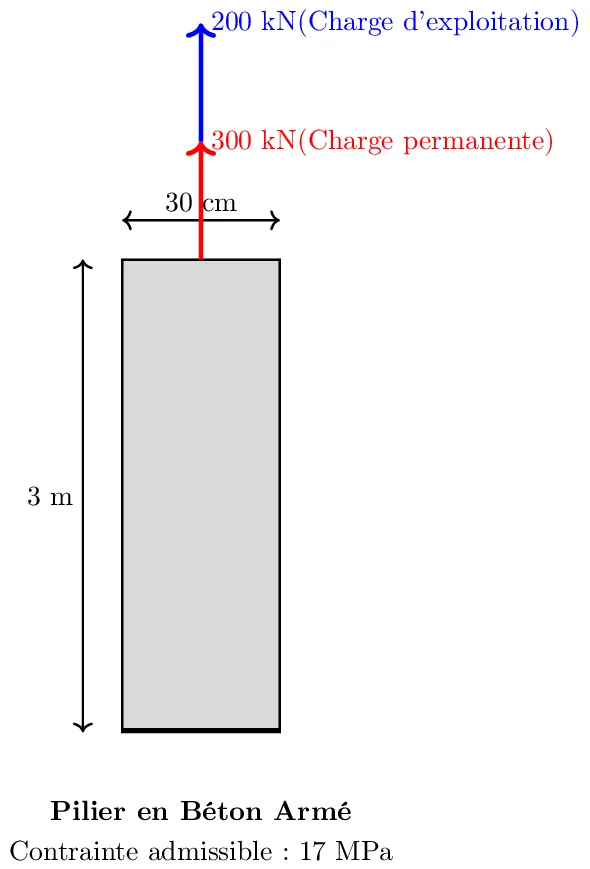
Un pilier en béton armé doit être construit pour soutenir une partie d’une structure dans un bâtiment de grande hauteur. Le pilier a une section transversale carrée et doit supporter une charge axiale due au poids des étages supérieurs ainsi qu’aux charges d’utilisation.

Comprendre le calcul de la Traction et compression exercice corrigé et le Calcul de la contrainte tangentielle, cliquez sur les liens.

Données:

Dimensions de la section transversale du pilier : 30 cm x 30 cm
Hauteur du pilier : 3 m
Charge permanente (Poids propre + poids des éléments structurels permanents) : 300 kN
Charge d’exploitation (mobilier, personnes, etc.) : 200 kN
Matériau : Béton armé, avec une contrainte admissible en compression de 17 MPa

Contrainte de Compression dans un Pilier

Questions:

1. Calcul de la charge totale supportée par le pilier

2. Calcul de l’aire de la section transversale du pilier

3. Calcul de la contrainte dans le pilier

4. Vérification de la contrainte admissible

Correction : Calcul de la Contrainte de Compression dans un Pilier

1. Calcul de la charge totale supportée par le pilier

Le pilier doit supporter à la fois la charge permanente (poids propre + éléments structurels) et la charge d’exploitation (mobilier, personnes, etc.). La charge totale est la somme de ces deux contributions.

Formule :

\[ P_{\text{total}} = P_{\text{permanente}} + P_{\text{exploitation}} \]

Données :

\(P_{\text{permanente}} = 300\ \text{kN}\)
\(P_{\text{exploitation}} = 200\ \text{kN}\)

Calcul :

\[ P_{\text{total}} = 300\ \text{kN} + 200\ \text{kN} \] \[ P_{\text{total}} = 500\ \text{kN} \]

2. Calcul de l’aire de la section transversale du pilier

Le pilier a une section carrée dont la longueur d’un côté est donnée. Pour obtenir l’aire, il suffit d’élever la longueur d’un côté au carré.

Formule :

\[ A = c^2 \]

Données :

\(c = 30\ \text{cm} = 0,3\ \text{m}\)

Calcul :

\[ A = (0,3\ \text{m})^2 = 0,09\ \text{m}^2 \]

3. Calcul de la contrainte dans le pilier

La contrainte (ou effort normal) dans le pilier est déterminée par le rapport de la charge totale à l’aire de la section transversale.

Formule :

\[ \sigma = \frac{P_{\text{total}}}{A} \]

Données :

\(P_{\text{total}} = 500\ \text{kN} = 500\,000\ \text{N}\)
\(\quad A = 0,09\ \text{m}^2\)

Calcul :

\[ \sigma = \frac{500\,000\ \text{N}}{0,09\ \text{m}^2} \] \[ \sigma \approx 5\,555\,556\ \text{N/m}^2 \] \[ \sigma \approx 5,56\ \text{MPa} \]

4. Vérification de la contrainte admissible

Pour que le pilier soit conforme, la contrainte calculée dans le pilier doit être inférieure ou égale à la contrainte admissible du béton armé.

Données :

\(\text{Contrainte calculée : } \sigma \approx 5,56\ \text{MPa}\)
\(\text{Contrainte admissible du béton armé : } \sigma_{\text{adm}} = 17\ \text{MPa}\)