Analyse des Contraintes par le Cercle de Mohr

Comprendre l’Analyse des Contraintes par le Cercle de Mohr

Dans le cadre d’un projet de génie civil, un ingénieur doit analyser les contraintes dans une poutre en béton armé soumise à diverses charges. La section considérée est soumise à des contraintes normales et des contraintes de cisaillement.

Pour évaluer l’état de contrainte en un point spécifique de cette section, l’ingénieur doit utiliser le cercle de Mohr.

Creation de Cercle de Mohr : Exercice – Corrigé, cliquez sur le lien.

Données:

Les contraintes en un point donné de la poutre sont les suivantes :

• Contrainte normale dans la direction \( x \) : \(\sigma_x = 30 \, \text{MPa}\)
• Contrainte normale dans la direction \( y \) : \(\sigma_y = -20 \, \text{MPa}\) (compression)
• Contrainte de cisaillement dans le plan \( xy \) : \(\tau_{xy} = 15 \, \text{MPa}\)

Questions:

1. Tracer le cercle de Mohr pour les contraintes données.

2. Déterminer les contraintes principales (maximales et minimales).

3. Déterminer les plans principaux (les orientations des plans où les contraintes de cisaillement sont nulles).

4. Calculer la contrainte de cisaillement maximale dans le matériau.

Correction : Analyse des Contraintes par le Cercle de Mohr

1. Tracer le cercle de Mohr pour les contraintes

Calcul du centre et du rayon du cercle de Mohr:

Le centre \( C \) du cercle de Mohr est donné par :

\[ C = \left( \frac{\sigma_x + \sigma_y}{2}, 0 \right) \]

Le rayon \( R \) du cercle de Mohr est :

\[ R = \sqrt{\left( \frac{\sigma_x – \sigma_y}{2} \right)^2 + \tau_{xy}^2} \]

• Calcul du centre:

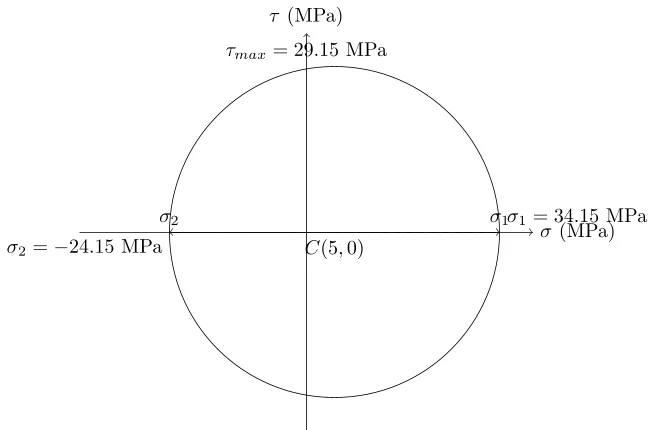
\[ C = \left( \frac{30 + (-20)}{2}, 0 \right) \] \[ C = \left( \frac{10}{2}, 0 \right) \] \[ C = (5, 0) \, \text{MPa} \]

• Calcul du rayon:

\[ R = \sqrt{\left( \frac{30 – (-20)}{2} \right)^2 + 15^2} \] \[ R = \sqrt{\left( \frac{50}{2} \right)^2 + 15^2} \] \[ R = \sqrt{25^2 + 15^2} \] \[ R = \sqrt{625 + 225} = \sqrt{850} \] \[ R \approx 29.15 \, \text{MPa} \]

Tracer le cercle de Mohr

Pour tracer le cercle de Mohr, on place le centre \( C \) à \( (5, 0) \) sur un graphique où l’axe horizontal représente les contraintes normales (\( \sigma \)) et l’axe vertical représente les contraintes de cisaillement (\( \tau \)). Ensuite, on trace un cercle avec ce centre et un rayon de \( 29.15 \, \text{MPa} \).

2. Détermination des contraintes principales

Les contraintes principales (\( \sigma_1 \) et \( \sigma_2 \)) sont les points où le cercle coupe l’axe des contraintes normales :

\[ \sigma_{1,2} = \frac{\sigma_x + \sigma_y}{2} \pm \sqrt{\left( \frac{\sigma_x – \sigma_y}{2} \right)^2 + \tau_{xy}^2} \]

Calcul des contraintes principales:

\[ \sigma_1 = 5 + 29.15 = 34.15 \, \text{MPa} \]

\[ \sigma_2 = 5 – 29.15 = -24.15 \, \text{MPa} \]

3. Détermination des orientations des plans principaux

L’angle \( \theta_p \) des plans principaux par rapport à la direction x est donné par :

\[ \tan(2\theta_p) = \frac{2\tau_{xy}}{\sigma_x – \sigma_y} \]

Calcul de l’angle des plans principaux:

\[ \tan(2\theta_p) = \frac{2 \times 15}{30 – (-20)} = \frac{30}{50} = 0.6 \] \[ 2\theta_p = \tan^{-1}(0.6) \approx 31^\circ \] \[ \theta_p \approx 15.5^\circ \]

4. Calcul de la contrainte de cisaillement maximale

La contrainte de cisaillement maximale \( \tau_{\text{max}} \) est égale au rayon du cercle de Mohr :

\[ \tau_{\text{max}} = R \approx 29.15 \, \text{MPa} \]

Conclusion:

• Les contraintes principales sont \( \sigma_1 = 34.15 \, \text{MPa} \) et \( \sigma_2 = -24.15 \, \text{MPa} \).
• Les plans principaux sont orientés à \( \theta_p \approx 15.5^\circ \) par rapport à la direction x.
• La contrainte de cisaillement maximale dans la poutre est \( \tau_{\text{max}} \approx 29.15 \, \text{MPa} \).

Analyse des Contraintes par le Cercle de Mohr

D’autres exercices de Rdm:

• Cercle de Mohr : Exercice – Corrigé
• Tracé d’Effort Tranchant et du Moment Fléchissant
• Calcul de la position de l’axe neutre