Tracé d’Effort Tranchant et du Moment Fléchissant
Comprendre le Tracé d’Effort Tranchant et du Moment Fléchissant
Vous êtes ingénieur en structure et devez analyser une poutre simplement appuyée utilisée dans la construction d’un petit pont piétonnier.
Cette poutre supporte à la fois son propre poids et des charges concentrées dues à l’utilisation potentiellement élevée lors d’événements locaux.
Pour comprendre le calcul de la Poutre encastrée et Diagramme des Moments, cliquez sur le lien.
Données de l’exercice:
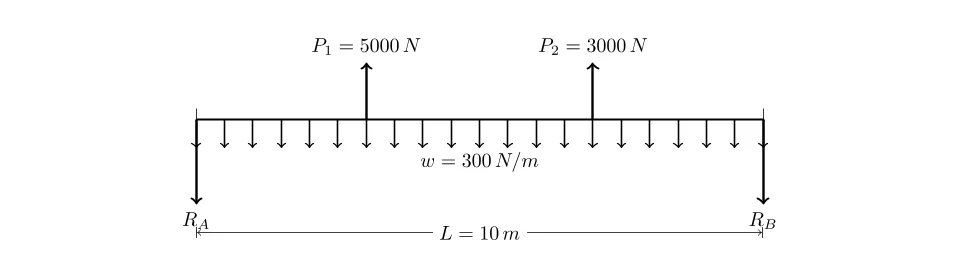
- Longueur de la poutre, \( L \): 10 m
- Poids propre de la poutre, \( w \) (réparti uniformément): 300 N/m
- Deux charges concentrées:
– \( P_1 = 5000 \, N \) située à 3 m du support de gauche.
– \( P_2 = 3000 \, N \) située à 7 m du support de gauche. - La poutre est simplement appuyée aux deux extrémités.
Questions:
1. Calcul des réactions aux appuis:
- Déterminez les réactions aux appuis \( R_A \) et \( R_B \).
2. Tracé du diagramme de l’effort tranchant (V):
- Tracez le diagramme de l’effort tranchant pour la poutre, en prenant en compte le poids propre et les charges concentrées.
3. Tracé du diagramme du moment fléchissant (M):
- Tracez le diagramme du moment fléchissant pour la poutre. Identifiez les points où le moment fléchissant est maximal et minimal.
4. Analyse des résultats:
- Discutez de l’importance des points de changement de signe dans les diagrammes d’effort tranchant et de moment fléchissant.
Correction : Tracé d’Effort Tranchant et du Moment Fléchissant
1. Calcul des réactions aux appuis
Données:
- Longueur de la poutre, \(L = 10 \, \text{m}\)
- Poids propre de la poutre, \(w = 300 \, \text{N/m}\)
- \(P_1 = 5000 \, \text{N}\) située à \(x_1 = 3 \, \text{m}\)
- \(P_2 = 3000 \, \text{N}\) située à \(x_2 = 7 \, \text{m}\)
Réactions aux appuis:
Les réactions \(R_A\) et \(R_B\) sont déterminées en utilisant les équilibres de moments et de forces verticales.
- Somme des moments autour de \(A\) (sens horaire positif):
\( R_B \times L = w \times \frac{L}{2} \times L + P_1 \times x_1 + P_2 \times x_2 \)
\( R_B \times 10 = 300 \times 5 \times 10 + 5000 \times 3 + 3000 \times 7 \)
\( R_B \times 10 = 15000 + 15000 + 21000 \)
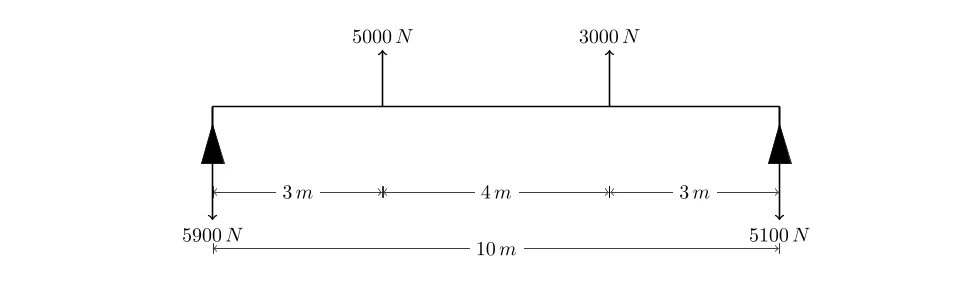
\( R_B \times 10 = 51000 \, \text{N} \quad \Rightarrow \quad R_B = 5100 \, \text{N}
\)
- Somme des forces verticales:
\( R_A + R_B = w \times L + P_1 + P_2 \)
\( R_A + 5100 = 300 \times 10 + 5000 + 3000 \)
\( R_A + 5100 = 3000 + 5000 + 3000 \)
\( R_A + 5100 = 11000 \, \text{N} \quad \Rightarrow \quad R_A = 5900 \, \text{N}
\)
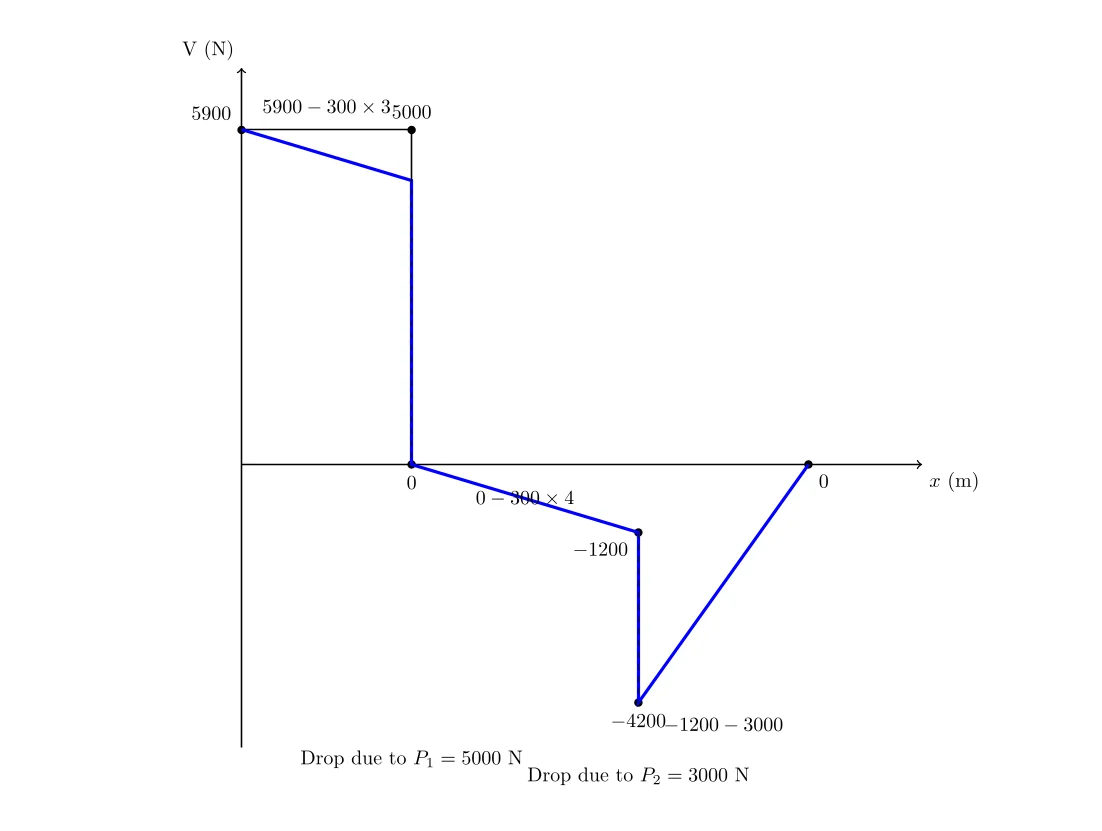
2. Tracé du diagramme de l’effort tranchant (V)
Le diagramme de l’effort tranchant commence à \(R_A\) et change à chaque charge.
- À \(x = 0\):
\[ V = +5900 \, \text{N} \]
- À \(x = 3\) (juste avant \(P_1\)):
\[ V = 5900 – 300 \times 3 \] \[ V = 5000 \, \text{N} \]
- À \(x = 3\) (juste après \(P_1\)):
\[ V = 5000 – 5000 = 0 \, \text{N} \]
- À \(x = 7\) (juste avant \(P_2\)):
\[ V = 0 – 300 \times (7-3) \] \[ V = -1200 \, \text{N} \]
- À \(x = 7\) (juste après \(P_2\)):
\[ V = -1200 – 3000 \] \[ V = -4200 \, \text{N} \]
- À \(x = 10\):
\[ V = -4200 + 300 \times (10-7) + 5100 \] \[ V = 0 \, \text{N} \]
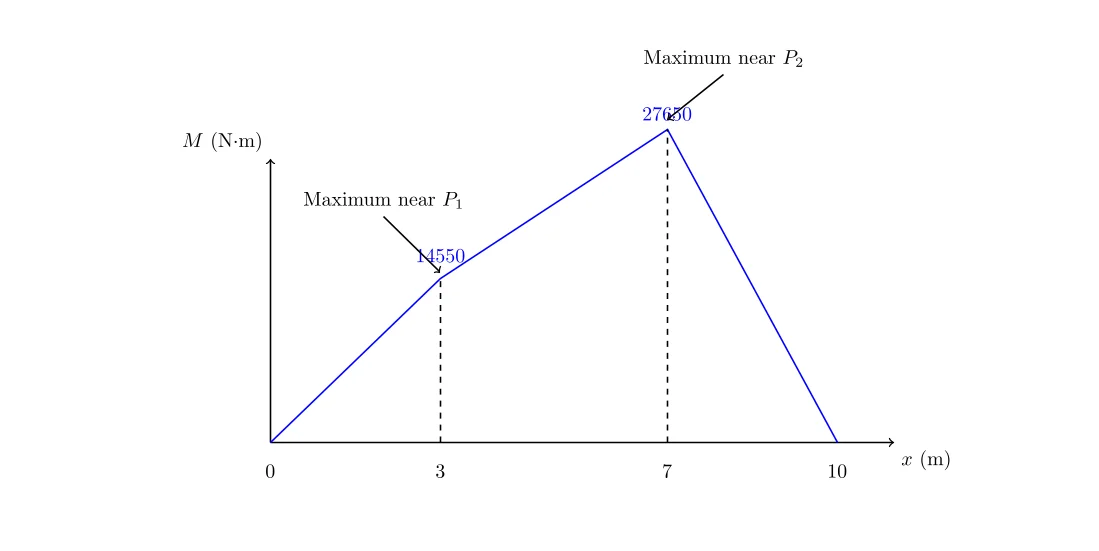
3. Tracé du diagramme du moment fléchissant (M)
Le moment fléchissant est nul aux supports et atteint des valeurs maximales/minimales à proximité des charges ou là où \(V = 0\).
- À \(x = 0\):
\[ M = 0 \]
- À \(x = 3\) (sous \(P_1\)):
\[ M = 5900 \times 3 – 300 \times \frac{3^2}{2} \] \[ M = 15900 – 1350 \] \[ M = 14550 \, N \cdot m \]
- À \(x = 7\) (sous \(P_2\)):
\[ M = 5000 \times 7 – 300 \times \frac{7^2}{2} \] \[ M = 35000 – 7350 \] \[ M = 27650 \, N \cdot m \]
4: Analyse des résultats
Les points de changement de signe dans le diagramme d’effort tranchant indiquent les emplacements des maxima et minima du moment fléchissant, ce qui est crucial pour identifier les zones critiques pour la conception en termes de flexion.
Les valeurs maximales du moment fléchissant mettent en évidence les zones potentielles de faiblesse où des renforcements peuvent être nécessaires.
Tracé d’Effort Tranchant et du Moment Fléchissant
D’autres exercices de Rdm:




Vous utilisez quelle règles pour les calculs de charge uniforme reparti
Bonjour,
Si vous avez un poids propre de la poutre (w) exprimé en newtons par mètre (N/m), et une longueur (L) de la poutre, alors la charge totale uniformément répartie (W) due au poids propre de la poutre sur toute sa longueur est calculée en multipliant le poids propre par la longueur de la poutre.
Ce génial
Un document très enrichissant pour nous les ingénieurs en structure. Merci infiniment les efforts.
Ce document est très intéressant
Bonsoir j’aimerais m’inscrire
Génial ce cours
Les exercices proposer est bonne, mais il faut nous laisser un lien de taux reseaux sociale pour la simplicité des partage
Vous pouvez aller sur notre page facebook nommé Étudiant Génie Civil ou cliquez sur ce lien pour aller sur notre facebook https://www.facebook.com/profile.php?id=100094864183912