Poutre encastrée
Comprendre le calcul d’une poutre encastrée :
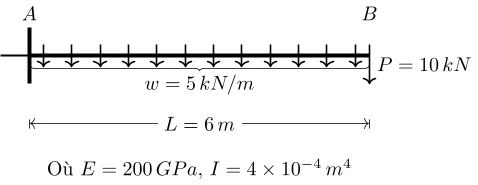
Une poutre encastrée en A supporte une charge uniformément répartie (UDL) sur toute sa longueur et une charge ponctuelle à son extrémité libre B.
Pour comprendre le calcul des Réactions d’Appui et Efforts Internes, cliquez sur le lien.
Données
- Longueur de la poutre, L = 6 mètres.
- Charge uniformément répartie (UDL), w = 5 kN/m.
- Charge ponctuelle en B, P = 10 kN.
- Module d’élasticité du matériau de la poutre, E = 200 GPa.
- Moment d’inertie de la section de la poutre, I = 4 x 10ˉ⁴ m⁴
Questions
- Calcul des Réactions d’Appui en A:
- Déterminer les réactions de la poutre en A (force verticale et moment).
- Diagramme des Moments Fléchissants:
- Dessiner le diagramme des moments fléchissants (M) pour la poutre. Identifier le moment maximal et son emplacement.
- Diagramme des Forces de Cisaillement:
- Établir le diagramme des forces de cisaillement (V) pour la poutre.
- Déflexion Maximale:
- Calculer la déflexion maximale de la poutre. Utiliser la formule de la déflexion pour une poutre encastrée avec une charge uniformément répartie et une charge ponctuelle.
- Analyse de la Sécurité:
- Estimer si la poutre est en sécurité contre la rupture, en considérant un moment de résistance maximal de la section de 120 kNm.
Correction : poutre encastrée
1. Calcul des Réactions d’Appui en A
Forces et Moments
- Charge Uniformément Répartie (UDL):
\[ w = 5 \, \text{kN/m} \]
- Force totale due à UDL:
\[ = w \times L \] \[ = 5 \times 6 = 30 \, \text{kN} \]
- Point d’application de la force UDL:
\[ = \frac{L}{2} = 3 \, \text{m} \]
- Charge Ponctuelle en B:
\[ P = 10 \, \text{kN} \]
- Point d’application:
\[ \text{En B (à } L = 6 \, \text{m de A)} \]
Équilibre Statique
Somme des Forces Verticales:
\[ \sum F_y = 0 \Rightarrow R_A – 30 – 10 = 0 \] \[ R_A = 40 \, \text{kN} \, \text{(vers le haut)} \]
Somme des Moments autour de A:
\[ \sum M_A = 0 \Rightarrow -30 \times 3 – 10 \times 6 + M_A = 0 \] \[ M_A = 90 + 60 = 150 \, \text{kNm} \] (moment encastré en A, sens anti-horaire)
2. Diagramme des Moments Fléchissants
- Le moment fléchissant varie le long de la poutre.
À l’extrémité encastrée (A), le moment est \(M_A = 150 \, \text{kNm}\). - À l’extrémité libre (B), le moment est nul.
- Le moment maximal se produit à l’encastrement, donc \(M_{\text{max}} = 150 \, \text{kNm}\).
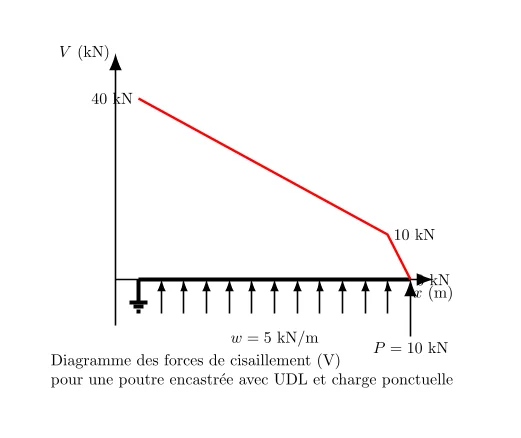
3. Diagramme des Forces de Cisaillement
- La force de cisaillement commence à \(40 \, \text{kN}\) en A (vers le haut).
- Elle diminue linéairement à cause de l’UDL et devient \(40 – 5 \times 6 = 10 \, \text{kN}\) juste avant le point B.
- En B, elle chute à \(0 \, \text{kN}\) à cause de la charge ponctuelle.
4. Déflexion Maximale
- Pour UDL (Charge Uniformément Répartie):
Formule de déflexion pour UDL:
\[ \delta_{\text{UDL}} = \frac{wL^4}{8EI} \]
Calcul avec substitution:
\[ \delta_{\text{UDL}} = \frac{5 \times 6^4}{8 \times 200 \times 10^9 \times 4 \times 10^{-4}} \] \[ \delta_{\text{UDL}} \approx 0.405 \, \text{mm} \]
- Pour Charge Ponctuelle:
Formule de déflexion pour charge ponctuelle:
\[ \delta_{P} = \frac{PL^2}{2EI} \]
Calcul avec substitution:
\[ \delta_{P} = \frac{10 \times 6^2}{2 \times 200 \times 10^9 \times 4 \times 10^{-4}} \] \[ \delta_{P} \approx 36 \, \text{mm} \]
- Déflexion Totale au Point B:
La déflexion totale est la somme des déflexions dues à l’UDL et à la charge ponctuelle:
\[ \delta_{\text{total}} \approx 0.405 \, \text{mm} + 36 \, \text{mm} \] \[ \delta_{\text{total}} \approx 36.405 \, \text{mm} \]
5. Analyse de la Sécurité
- Le moment fléchissant maximal est \(M_{\text{max}} = 150 \, \text{kNm}\).
- Le moment de résistance maximal de la section est \(M_{\text{res}} = 120 \, \text{kNm}\).
Conclusion: Puisque \(M_{\text{max}} > M_{\text{res}}\) (\(150 \, \text{kNm} > 120 \, \text{kNm}\)), la poutre n’est pas en sécurité et risque de rompre.
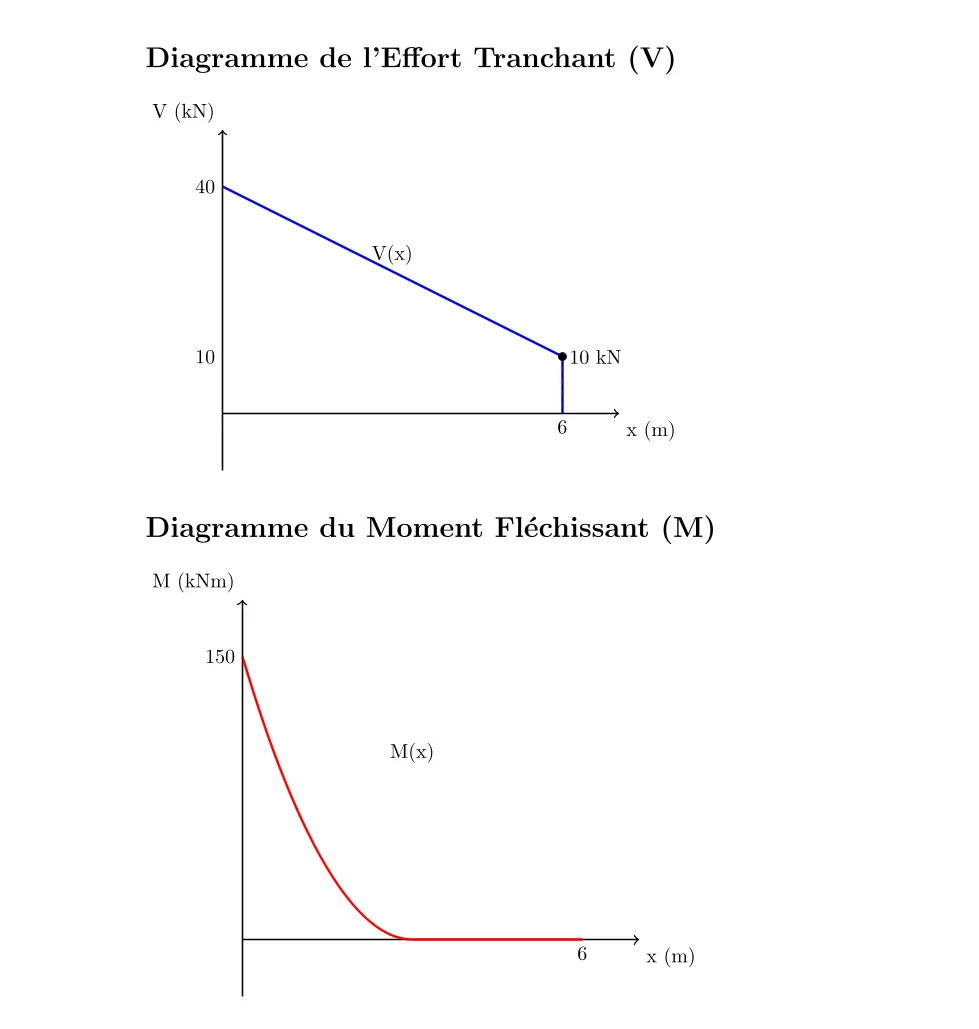
Diagramme des Forces de Cisaillement
Poutre encastrée
D’autres exercices de résistance des materiaux :




0 commentaires