Réactions d’Appui et Efforts Internes

Comprendre les Réactions d’Appui et Efforts Internes

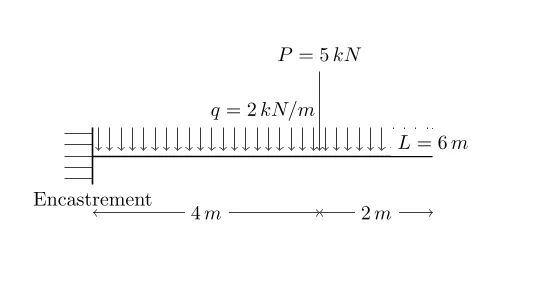
Considérons une poutre encastrée-libre d’une longueur $L=6\text{m}$. La poutre est soumise à une charge uniformément répartie $q=2\text{kN/m}$ sur toute sa longueur, ainsi qu’à une charge ponctuelle $P=5\text{kN}$ appliquée à $2\text{m}$ de l’extrémité libre de la poutre.

Pour comprendre le Diagrammes d’Effort Tranchant et Moment et le calcul du Déplacement de l’Extrémité Libre d’une poutre, cliquez sur les liens.

Questions:

1. Calculer les réactions d’appui à l’encastrement (à savoir, la réaction verticale (\(R_y\)), la réaction horizontale (\(R_x\)), et le moment d’encastrement (\(M\))
2. Dessiner les diagrammes de moments fléchissants, d’efforts tranchants, et d’efforts normaux pour la poutre, en utilisant les réactions calculées.

Correction : Réactions d’Appui et Efforts Internes

Données:

• Longueur de la poutre, \(L = 6\, \text{m}\)
• Charge uniformément répartie, \(q = 2\, \text{kN/m}\)
• Charge ponctuelle, \(P = 5\, \text{kN}\)
• Position de la charge ponctuelle depuis l’extrémité libre, \(a = 2\, \text{m}\)

1. Calcul des réactions d’appui

Pour une poutre encastrée-libre, les réactions d’appui seront calculées à l’encastrement. On considère que l’extrémité libre ne fournit pas de réaction verticale, horizontale, ou de moment.

Réaction verticale \(R_y\):

La réaction verticale à l’encastrement doit équilibrer les forces verticales dues à la charge répartie et à la charge ponctuelle.

\[ R_y = qL + P \] \[
R_y = (2\, \text{kN/m} \times 6\, \text{m}) + 5\, \text{kN} \] \[
R_y = 12\, \text{kN} + 5\, \text{kN} \] \[
R_y = 17\, \text{kN} \]

Réaction horizontale \(R_x\):

Dans ce problème, aucune charge horizontale n’est appliquée, donc \(R_x = 0\).

Moment d’encastrement \(M\):

Le moment d’encastrement est causé par la charge répartie et la charge ponctuelle. Le moment dû à la charge répartie est calculé comme le moment d’une force équivalente \(qL\) appliquée au centre de la charge répartie, soit \(L/2\) depuis l’encastrement.

Le moment dû à la charge ponctuelle est \(P\) multiplié par sa distance de l’encastrement, soit \(L – a\).

\[ M = \frac{qL^2}{2} + P(L – a) \] \[ M = \frac{2\, \text{kN/m} \times (6\, \text{m})^2}{2} + 5\, \text{kN} \times (6\, \text{m} – 2\, \text{m}) \] \[ M = 36\, \text{kNm} + 20\, \text{kNm} \] \[ M = 56\, \text{kNm} \]

2. Dessin des Diagrammes

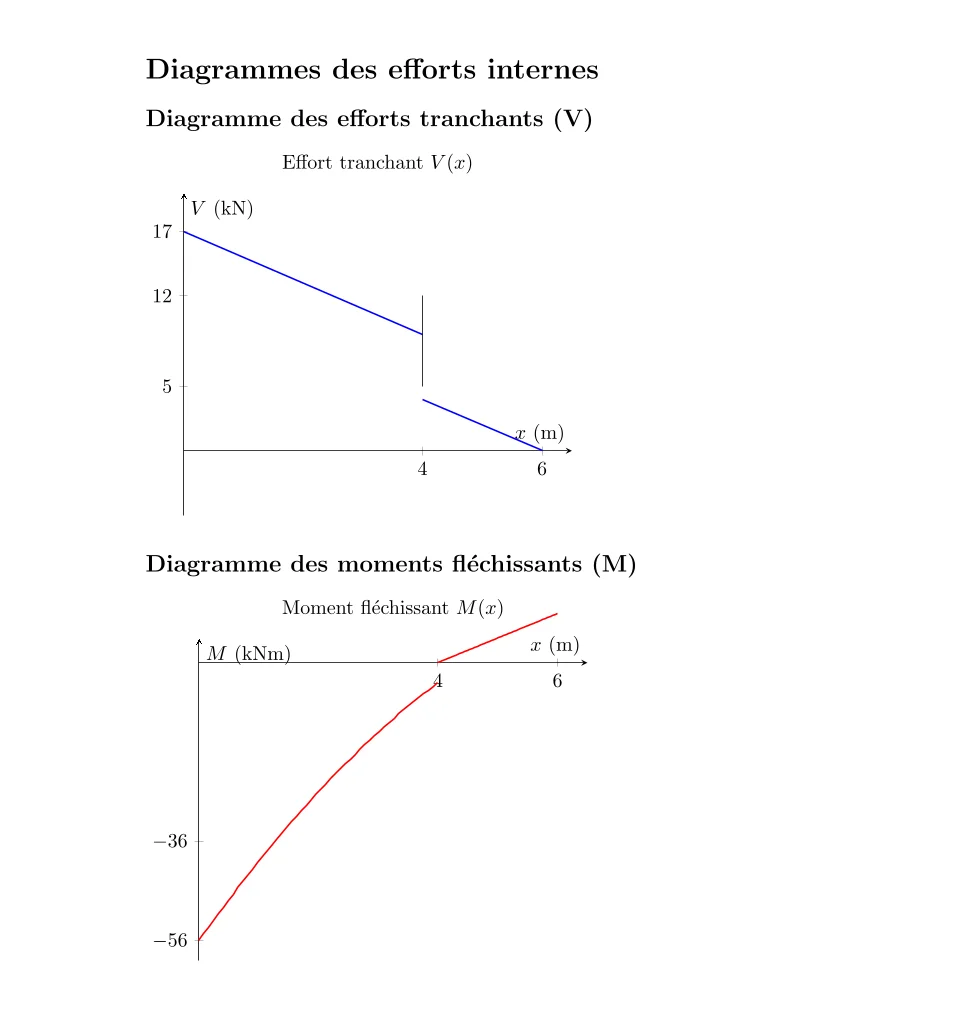
Diagramme des efforts tranchants (V):

Commence à \(+17\, \text{kN}\) à l’encastrement, diminue linéairement à cause de la charge répartie, et chute soudainement à \(+5\, \text{kN}\) à la position de la charge ponctuelle.

Diagramme des moments fléchissants (M):

Commence à \(-56\, \text{kNm}\) à l’encastrement (moment négatif car il tend à fléchir la poutre dans le sens horaire), atteint un maximum (en valeur absolue) où la pente du diagramme V est nulle, puis diminue jusqu’à zéro à l’extrémité libre.

Diagramme des efforts normaux (N):

Reste à zéro dans tout le système car il n’y a pas de charge axiale appliquée.

Réactions d’Appui et Efforts Internes

D’autres exercices de Rdm:

• Diagrammes d’Effort Tranchant et Moment
• Cercle de Mohr : Exercice – Corrigé
• Calcul de la contrainte de flexion