Cercle de Mohr : Exercice – Corrigé
Contexte de calcul
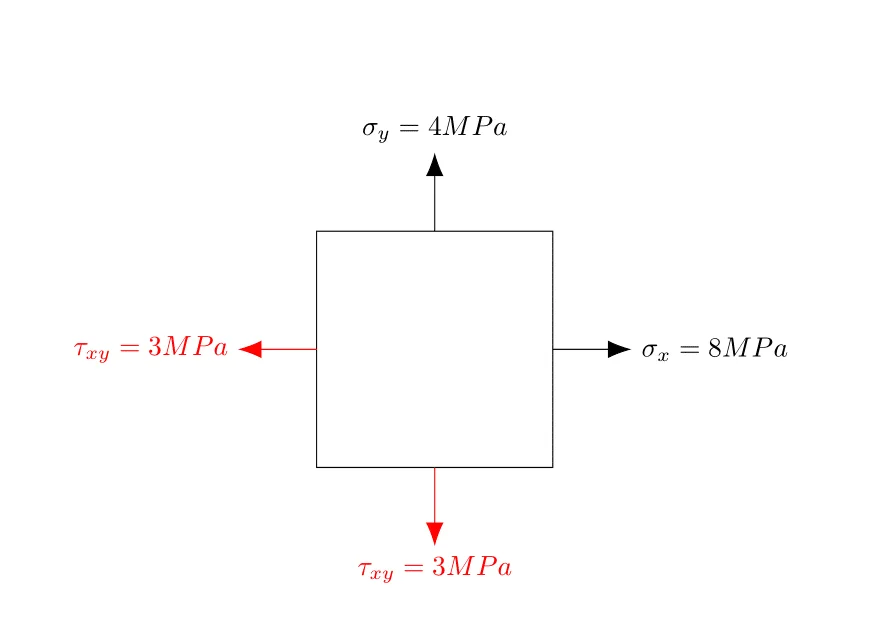
Une poutre est soumise à des contraintes plane. À un certain point de cette poutre, les contraintes normales sur les faces horizontales et verticales sont \( \sigma_x = 8 \text{ MPa} \) et \( \sigma_y = 4 \text{ MPa} \) respectivement.
La contrainte de cisaillement sur le plan horizontal est \( \tau_{xy} = 3 \text{ MPa} \) (dans le sens positif en tournant dans le sens contraire des aiguilles d’une montre).
Pour comprendre le calcul d’une contrainte principale et d’une contrainte de cisaillement, cliquez sur les liens.
Questions:
- Représentez ces contraintes sur un élément de stress.
- Calculez le rayon et le centre du Cercle de Mohr.
- Déterminez les contraintes principales.
- Trouvez les angles d’orientation de ces contraintes principales.
Correction du cercle de mohr
1. Représentation des Contraintes:
Sur la face horizontale, la contrainte normale est de \(8 \text{ MPa}\) vers la droite et la contrainte de cisaillement est de \(3 \text{ MPa}\) vers le haut.
Sur la face verticale, la contrainte normale est de \(4 \text{ MPa}\) vers le haut et la contrainte de cisaillement est de \(3 \text{ MPa}\) vers la droite.
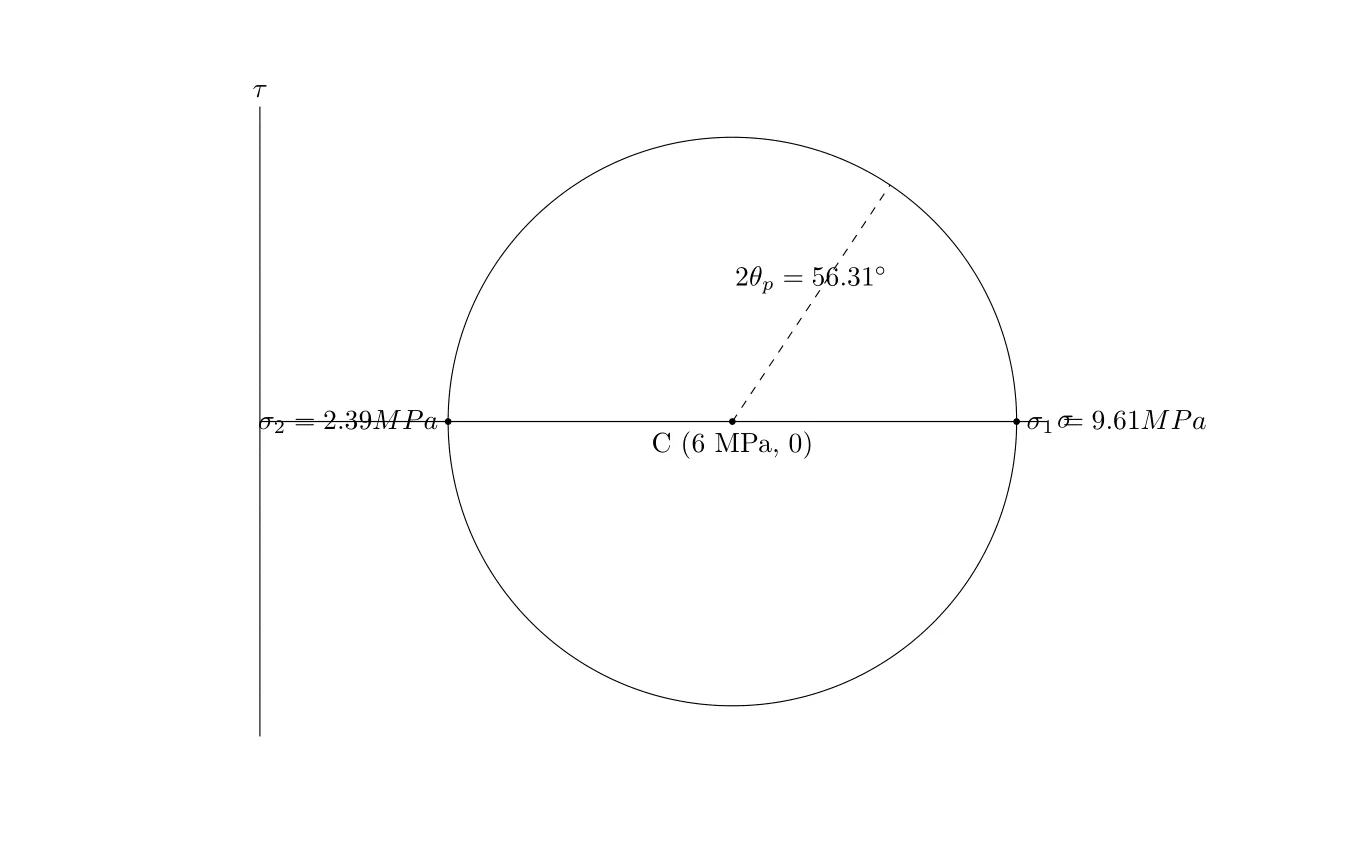
2. Centre et Rayon du Cercle de Mohr:
Le centre du cercle, \(C\), est donné par :
\[ C = \frac{\sigma_x + \sigma_y}{2} \] \[ C = \frac{8 \text{ MPa} + 4 \text{ MPa}}{2} \] \[ C = 6 \text{ MPa} \]
Le rayon du cercle, \(R\), est :
\[ R = \sqrt{\left(\frac{\sigma_x – \sigma_y}{2}\right)^2 + \tau_{xy}^2} \] \[ R = \sqrt{2^2 + 3^2} \] \[ R = \sqrt{13} \text{ MPa} \] \[ R \approx 3.61 \text{ MPa} \] \[ R \approx 3.61 \text{ MPa} \]
3. Contraintes Principales:
\[ \sigma_1 = C + R \] \[ \sigma_1 = 6 \text{ MPa} + 3.61 \text{ MPa} \] \[ \sigma_1 = 9.61 \text{ MPa} \]
\[ \sigma_2 = C – R \] \[ \sigma_2 = 6 \text{ MPa} – 3.61 \text{ MPa} \] \[ \sigma_2 = 2.39 \text{ MPa} \]
4. Angles d’Orientation:
L’angle d’orientation, \(2\theta_p\), est donné par:
\[ 2\theta_p = \tan^{-1}\left(\frac{\tau_{xy}}{\frac{\sigma_x – \sigma_y}{2}}\right) \] \[ 2\theta_p = \tan^{-1}\left(\frac{3}{2}\right) \]
\[ 2\theta_p \approx 56.31^\circ \]
Ainsi, \[ \theta_p \approx 28.16^\circ \]
illustrations graphiques à la correction
élément de stress
Cercle de mohr
D’autres exercices de Rdm:




0 commentaires