Analyse des Forces dans une Poutre

Comprendre l’Analyse des Forces dans une Poutre

Vous êtes ingénieur civil et vous travaillez sur la conception d’une passerelle piétonne au-dessus d’un petit ruisseau. La passerelle est soutenue par une poutre en acier simplement appuyée à ses deux extrémités. La poutre doit supporter non seulement son propre poids, mais aussi le poids des piétons qui peuvent l’utiliser simultanément ainsi que celui des éléments de sécurité et de décoration.

Comprendre le Calcul l’effort tranchant et le moment, cliquez sur le lien.

Données de l’exercice:

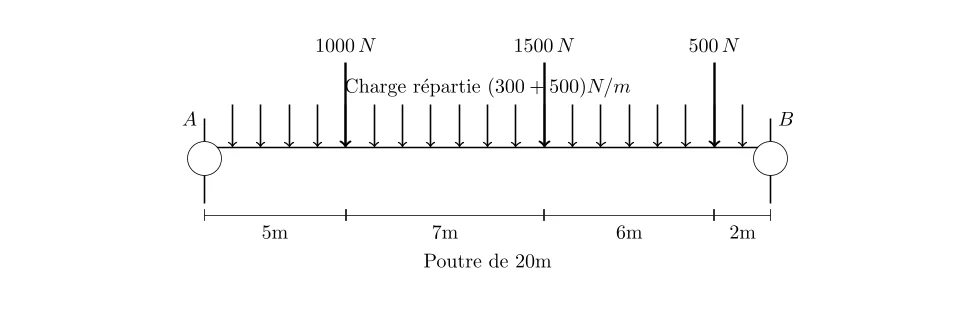
Longueur de la poutre, \( L \): 20 mètres
Poids propre de la poutre (charge uniformément répartie), \( w \): 300 N/m
Charge due aux piétons (modélisée comme une charge uniformément répartie supplémentaire), \( w_p \): 500 N/m
Poids des éléments de sécurité et décoration (considérés comme des charges ponctuelles à divers points), répartis comme suit:

– \( P_1 \): 1000 N au point situé à 5 m du support gauche

– \( P_2 \): 1500 N au point situé à 12 m du support gauche

– \( P_3 \): 500 N au point situé à 18 m du support gauche

Questions:

1. Calcul des réactions d’appui :

Déterminez les réactions aux appuis \( R_A \) et \( R_B \).

2. Diagramme des moments fléchissants :

Tracez le diagramme des moments fléchissants pour la poutre.
Identifiez le point où le moment fléchissant est maximal.

3. Diagramme des forces tranchantes :

Tracez le diagramme des forces tranchantes pour la poutre.
Identifiez les points où la force tranchante change de signe.

Correction : Analyse des Forces dans une Poutre

1. Calcul des Réactions d’Appui

Calcul préliminaire – Charge Uniformément Répartie Totale

Les deux charges uniformes s’additionnent :

\[ w_{\text{tot}} = w + w_p \] \[ w_{\text{tot}} = 300 + 500 \] \[ w_{\text{tot}} = 800 \,\text{N/m} \]

La charge totale uniformément répartie sur la poutre est donc :

\[ F_{\text{UR}} = w_{\text{tot}} \times L \] \[ F_{\text{UR}} = 800 \,\text{N/m} \times 20\, \text{m} \] \[ F_{\text{UR}} = 16\,000 \,\text{N} \]

Les charges ponctuelles totalisent :

\[ F_{\text{ponct}} = P_1 + P_2 + P_3 \] \[ F_{\text{ponct}} = 1000 + 1500 + 500 \] \[ F_{\text{ponct}} = 3000 \,\text{N} \]

La charge verticale totale appliquée sur la poutre est alors :

\[ F_{\text{total}} = 16\,000 + 3000 \] \[ F_{\text{total}} = 19\,000 \,\text{N} \]

Équations d’Équilibre

Pour une poutre simplement appuyée, les deux réactions d’appuis, notées \( R_A \) et \( R_B \), doivent satisfaire :

1. Somme des forces verticales :

\[ R_A + R_B = F_{\text{total}} = 19\,000 \,\text{N} \]

2. Somme des moments autour du support A :

En prenant le moment autour de A, la contribution de la charge uniformément répartie se fait en considérant que l’ensemble de la charge agit en son centre de gravité, c’est-à-dire à \( \frac{L}{2} \) (10 m). Pour chaque charge ponctuelle, le bras de levier est la distance par rapport à A.

\[ R_B \times L – \left(F_{\text{UR}} \times \frac{L}{2}\right) – \left[P_1 \times 5 + P_2 \times 12 + P_3 \times 18\right] = 0 \]

Substitution des Valeurs

Moment dû à la charge uniforme :

\[ = 16\,000\, \text{N} \times 10\, \text{m} \] \[ = 160\,000 \,\text{N·m} \]

Moments des charges ponctuelles :

\( P_1 \) : \( 1000\, \text{N} \times 5\, \text{m} = 5\,000 \,\text{N·m} \)
\( P_2 \) : \( 1500\, \text{N} \times 12\, \text{m} = 18\,000 \,\text{N·m} \)
\( P_3 \) : \( 500\, \text{N} \times 18\, \text{m} = 9\,000 \,\text{N·m} \)

Le total des moments des charges ponctuelles est :

\[ = 5\,000 + 18\,000 + 9\,000 \] \[ = 32\,000 \,\text{N·m} \]

L’équation du moment devient :

\[ R_B \times 20 – 160\,000 – 32\,000 = 0 \] \[ \Rightarrow \quad R_B \times 20 = 192\,000 \,\text{N·m} \]

\[ \Rightarrow \quad R_B = \frac{192\,000}{20} = 9600 \,\text{N} \]

Ensuite, par la somme des forces verticales :

\[ R_A = 19\,000 – R_B \] \[ R_A = 19\,000 – 9600 \] \[ R_A = 9400 \,\text{N} \]

Conclusion Réactions :
\( R_A = 9400 \,\text{N} \) et \( R_B = 9600 \,\text{N} \).

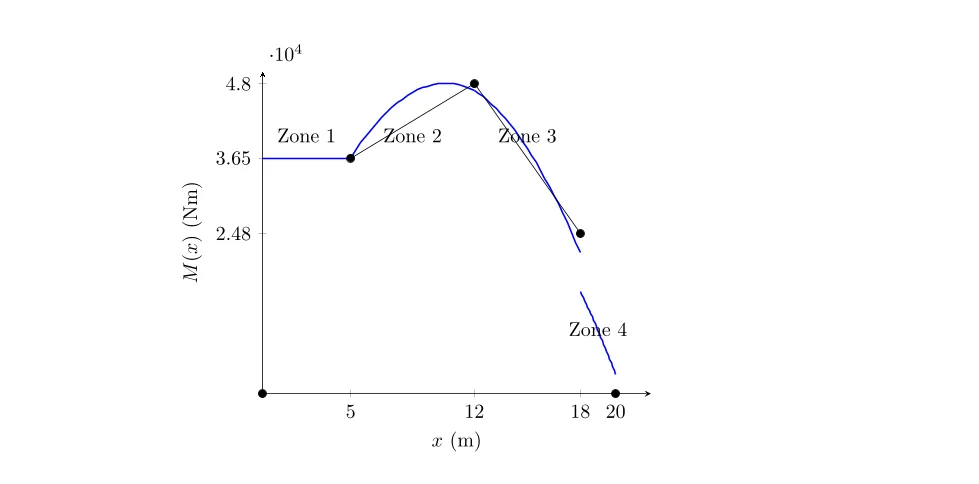
2. Diagramme des Moments Fléchissants

Principe et Formulation

Pour un point quelconque \( x \) le long de la poutre, le moment fléchissant \( M(x) \) se calcule par :

\[ M(x) = R_A \times x – \frac{w_{\text{tot}}\, x^2}{2} – \sum_{\{i \,|\, x > a_i\}} P_i\,(x – a_i) \]

où \( a_i \) est la position du \( i^\text{ème} \) chargement ponctuel et la somme ne porte que sur les charges déjà rencontrées à partir de A.

Nous découpant la poutre en segments en fonction des positions des charges ponctuelles :

Segment 1 : \( 0 \le x < 5\, \text{m} \)

Aucune charge ponctuelle n’est encore appliquée.

\[ M(x) = 9400\,x – \frac{800\,x^2}{2} \] \[ M(x) = 9400\,x – 400\,x^2 \]

À \( x = 5\, \text{m} \) :

\[ M(5) = 9400 \times 5 – 400 \times 25 \] \[ M(5) = 47\,000 – 10\,000 \] \[ M(5) = 37\,000 \,\text{N·m} \]

Segment 2 : \( 5 \le x < 12\, \text{m} \)

La charge ponctuelle \( P_1 = 1000\, \text{N} \) (à 5 m) intervient.

\[ M(x) = 9400\,x – 400\,x^2 – 1000\,(x – 5) \]

À \( x = 5\, \text{m} \) (limite gauche) :

\[ M(5) = 9400 \times 5 – 400 \times 25 – 1000\,(0) \] \[ M(5) = 37\,000 \,\text{N·m} \]

À \( x = 12\, \text{m} \) :

\[ M(12) = 9400 \times 12 – 400 \times 144 – 1000\,(12 – 5) \] \[ M(12) = 112\,800 – 57\,600 – 7\,000 \] \[ M(12) = 48\,200 \,\text{N·m} \]

Segment 3 : \( 12 \le x < 18\, \text{m} \)

Les charges ponctuelles \( P_1 \) et \( P_2 \) (à 5 m et 12 m) sont actives.

\[ M(x) = 9400\,x – 400\,x^2 – 1000\,(x – 5) – 1500\,(x – 12) \]

À \( x = 12\, \text{m} \) :

\[ M(12) = 112\,800 – 57\,600 – 7\,000 – 1500\,(0) \] \[ M(12) = 48\,200 \,\text{N·m} \]

À \( x = 18\, \text{m} \) :

\[ M(18) = 9400 \times 18 – 400 \times 324 – 1000\,(18 – 5) – 1500\,(18 – 12) \] \[ M(18) = 169\,200 – 129\,600 – 13\,000 – 9\,000 \] \[ M(18) = 17\,600 \,\text{N·m} \]

Segment 4 : \( 18 \le x \le 20\, \text{m} \)

Toutes les charges sont prises en compte (\( P_1 \), \( P_2 \) et \( P_3 \)).

\[ M(x) = 9400\,x – 400\,x^2 – 1000\,(x – 5) – 1500\,(x – 12) – 500\,(x – 18) \]

À \( x = 18\, \text{m} \) :

\[ M(18) = 17\,600 \,\text{N·m} \] ( cohérent avec le segment précédent )

À \( x = 20\, \text{m} \) (appui droit) :

\[ M(20) = 9400 \times 20 – 400 \times 400 – 1000\,(20 – 5) – 1500\,(20 – 12) – 500\,(20 – 18) \] \[ M(20) = 188\,000 – 160\,000 – 15\,000 – 12\,000 – 1000 \] \[ M(20) = 0 \,\text{N·m} \]
(La condition d’appui sans moment fléchissant est vérifiée.)

Point de Moment Maximum

Pour déterminer le maximum, on peut rechercher l’annulation de la dérivée dans la région continue. Prenons par exemple le Segment 2 où la fonction est :

\[ M(x) = 9400\,x – 400\,x^2 – 1000\,(x – 5) \]

La dérivée est :

\[ \frac{dM}{dx} = 9400 – 800\,x – 1000 \] \[ \frac{dM}{dx} = 8400 – 800\,x \]

Posons \(\frac{dM}{dx} = 0\) :

\[ 8400 – 800\,x = 0 \] \[ \Rightarrow \quad x = \frac{8400}{800} = 10.5 \,\text{m} \]

Calcul de \( M(10.5) \) :

\[ M(10.5) = 9400 \times 10.5 – 400 \times (10.5)^2 – 1000\,(10.5 – 5) \] \[ M(10.5) = 98\,700 – 400 \times 110.25 – 1000 \times 5.5 \] \[ M(10.5) = 98\,700 – 44\,100 – 5\,500 \] \[ M(10.5) = 49\,100 \,\text{N·m} \]

Conclusion Diagramme des Moments :
Le moment fléchissant est nul aux appuis (\(x=0\) et \(x=20\, \text{m}\)), atteint une valeur de \(37\,000\, \text{N·m}\) en \(x=5\, \text{m}\), \(48\,200\, \text{N·m}\) en \(x=12\, \text{m}\), et atteint son maximum de \textbf{\(49\,100\, \text{N·m}\) à \(x=10.5\, \text{m}\)}.

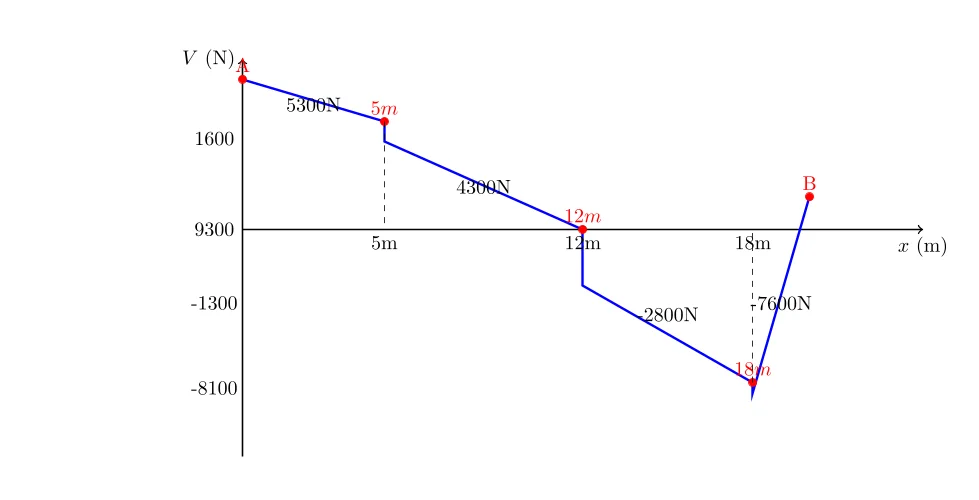
3. Diagramme des Forces Tranchantes

Principe et Formulation

La force tranchante \( V(x) \) est obtenue par l’équation d’équilibre vertical. Pour un point \( x \) de la poutre, avant application d’une charge ponctuelle (en tenant compte de la répartition des charges uniformes) :

\[ V(x) = R_A – w_{\text{tot}}\,x – \sum_{\{i\,|\, x > a_i\}} P_i \]

Les valeurs subissent des sauts aux points d’application des charges ponctuelles.

Calcul Par Segment

Segment 1 : \( 0 \le x < 5\, \text{m} \)

Aucune charge ponctuelle n’est encore appliquée.

\[ V(x) = R_A – w_{\text{tot}}\,x \] \[ V(x) = 9400 – 800\,x \]

À \( x = 0\, \text{m} \) :

\[ V(0) = 9400 \,\text{N} \]

À \( x = 5\, \text{m} \) :

\[ V(5) = 9400 – 800 \times 5 \] \[ V(5) = 9400 – 4000 \] \[ V(5) = 5400 \,\text{N} \]

Segment 2 : \( 5 \le x < 12\, \text{m} \)

Dès le point \( x = 5\, \text{m} \), la charge \( P_1 = 1000\, \text{N} \) est appliquée, ce qui induit une chute instantanée :

\[ V(5^+) = 5400 – 1000 \] \[ V(5^+) = 4400 \,\text{N} \]

Pour \( x > 5\, \text{m} \) :

\[ V(x) = 9400 – 800\,x – 1000 \] \[ V(x) = 8400 – 800\,x \]

À \( x = 10.5\, \text{m} \) (point de changement de signe potentiel) :

\[ V(10.5) = 8400 – 800 \times 10.5 \] \[ V(10.5) = 8400 – 8400 \] \[ V(10.5) = 0 \,\text{N} \]

Segment 3 : \( 12 \le x < 18\, \text{m} \)

À \( x = 12\, \text{m} \), on intègre la charge \( P_2 = 1500\, \text{N} \) :

\[ V(12^+) = \left[8400 – 800 \times 12\right] – 1500 \]

Calculons :

\[ 8400 – 9600 = -1200 \] puis} \[ -1200 – 1500 = -2700 \,\text{N} \]

Pour \( x > 12\, \text{m} \) :

\[ V(x) = 9400 – 800\,x – 1000 – 1500 \] \[ V(x) = 6900 – 800\,x \]

À \( x = 18\, \text{m} \) :

\[ V(18) = 6900 – 800 \times 18 \] \[ V(18) = 6900 – 14\,400 \] \[ V(18) = -7500 \,\text{N} \]

Segment 4 : \( 18 \le x \le 20\, \text{m} \)

À \( x = 18\, \text{m} \), la charge \( P_3 = 500\, \text{N} \) est appliquée :

\[ V(18^+) = -7500 – 500 \] \[ V(18^+) = -8000 \,\text{N} \]

Pour \( x > 18\, \text{m} \) :

\[ V(x) = 9400 – 800\,x – 1000 – 1500 – 500 \] \[ V(x) = 6400 – 800\,x \]

À \( x = 20\, \text{m} \) :

\[ V(20) = 6400 – 800 \times 20 \] \[ V(20) = 6400 – 16\,000 \] \[ V(20) = -9600 \,\text{N} \]

Ce résultat est cohérent avec le fait que, juste à droite de l’appui B, la force tranchante subit un saut de \( +R_B = +9600\, \text{N} \) pour annuler et obtenir \( V = 0 \) en dehors de la poutre.

Points de Changement de Signe

Dans le Segment 2, la force tranchante passe de positive à nulle à \( x = 10.5\, \text{m} \), ce qui correspond au moment fléchissant maximum.
Les sauts (discontinuités) se produisent aux points d’application des charges ponctuelles, c’est-à-dire en \( x = 5\, \text{m} \), \( x = 12\, \text{m} \) et \( x = 18\, \text{m} \).

Conclusion Forces Tranchantes :

Segment 1 (\(0 \le x < 5\, \text{m}\)) : \( V(x) = 9400 – 800\,x \)
Segment 2 (\(5 \le x < 12\, \text{m}\)) : \( V(x) = 8400 – 800\,x \) avec \( V(10.5) = 0\, \text{N} \) (point de changement de signe)
Segment 3 (\(12 \le x < 18\, \text{m}\)) : \( V(x) = 6900 – 800\,x \)
Segment 4 (\(18 \le x \le 20\, \text{m}\)) : \( V(x) = 6400 – 800\,x \)