Déplacement de l’Extrémité Libre
Comprendre le déplacement de l’Extrémité Libre
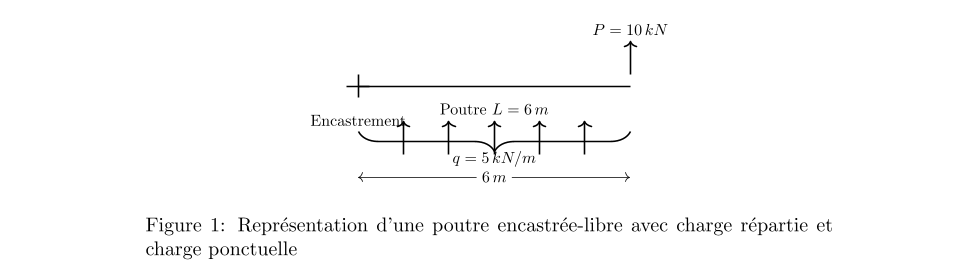
Considérons une poutre encastrée-libre, c’est-à-dire une poutre avec une extrémité encastrée et l’autre extrémité libre.
Cette poutre est soumise à une charge uniformément répartie et à une charge ponctuelle à son extrémité libre.
Pour comprendre le Tracé d’Effort Tranchant et du Moment Fléchissant, cliquez sur le lien.
Données de la Poutre:
Les caractéristiques de la poutre et les charges appliquées sont les suivantes :
- Longueur de la poutre, L = 6 m
- Module d’élasticité du matériau de la poutre, E = 210 GPa
- Moment d’inertie de la section transversale, I = 8000 \({cm}^4\)
- Charge uniformément répartie, q = 5 kN/m
- Charge ponctuelle à l’extrémité libre, P = 10 kN
Instructions:
- Calcul des Réactions d’Appui: Déterminer les réactions au niveau de l’encastrement.
- Diagramme des Moments Fléchissants (DMF): Établir le DMF pour la poutre.
- Déplacement de l’Extrémité Libre: Calculer le déplacement vertical de l’extrémité libre de la poutre.
Correction : déplacement de l’Extrémité Libre
Étape 1: Calcul des Réactions d’Appui
Pour une poutre encastrée-libre, les réactions d’appui se composent d’une force verticale et d’un moment à l’encastrement.
1. Force Verticale à l’Encastrement (R)
La force totale due à la charge uniformément répartie est
\[ = q \times L \] \[ = 5 \, \text{kN/m} \times 6 \, \text{m} \] \[ = 30 \, \text{kN} \]
Cette force agit au centre de gravité de la charge répartie, qui se situe au milieu de la poutre (à 3 m de l’encastrement). En plus, il y a une charge ponctuelle de 10 kN à l’extrémité libre.
L’équation d’équilibre verticale est :
\[ R = qL + P \] \[ R = 30 \, \text{kN} + 10 \, \text{kN} \] \[ R = 40 \, \text{kN} \]
2. Moment à l’Encastrement (M)
Le moment dû à la charge uniformément répartie est \( \frac{qL^2}{2} \) et le moment dû à la charge ponctuelle est \( PL \)
Ainsi,
\[ M = \frac{qL^2}{2} + PL \] \[ M = \frac{5 \times 6^2}{2} + 10 \times 6 \] \[ M = 90 + 60 \] \[ M = 150 \, \text{kNm} \]
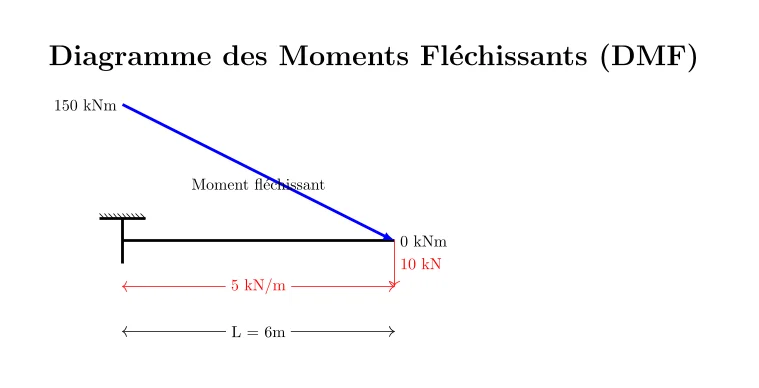
Étape 2: Diagramme des Moments Fléchissants (DMF)
Le DMF pour une poutre encastrée-libre avec une charge uniformément répartie et une charge ponctuelle à l’extrémité se calcule de la manière suivante :
- À l’encastrement (point A, à \(x=0\)), le moment est maximal et égal à 150 kNm (calculé ci-dessus).
- Le moment diminue linéairement le long de la poutre à cause de la charge uniformément répartie.
- À l’extrémité libre (point B, à \(x=L\)), le moment est nul.
Le DMF est donc une courbe qui commence à 150 kNm à l’encastrement, décroît linéairement et atteint 0 kNm à l’extrémité libre.
Étape 3: Déplacement de l’Extrémité Libre
Déplacement dû à la Charge Uniformément Répartie \((\delta_q)\):
Le déplacement dû à la charge uniformément répartie est calculé par la formule :
\[\delta_q = \frac{qL^4}{8EI} \] \[\delta_q = \frac{5 \times 10^3 \times 6^4}{8 \times 210 \times 10^9 \times 8000 \times 10^{-8}} \] \[\delta_q \approx 4.82 \, \text{mm}\]
Déplacement dû à la Charge Ponctuelle \((\delta_P)\):
Le déplacement dû à la charge ponctuelle est calculé par la formule :
\[\delta_P = \frac{PL^3}{3EI} \] \[\delta_P = \frac{10 \times 10^3 \times 6^3}{3 \times 210 \times 10^9 \times 8000 \times 10^{-8}} \] \[\delta_P \approx 4.29 \, \text{mm}\]
Déplacement Total à l’Extrémité Libre:
Le déplacement total à l’extrémité libre est donc la somme des deux déplacements calculés précédemment :
\[\delta_{\text{total}} = \delta_q + \delta_P \] \[\delta_{\text{total}} \approx 4.82 \, \text{mm} + 4.29 \, \text{mm} \] \[\delta_{\text{total}} \approx 9.11 \, \text{mm}\]
Résumé:
- Les réactions à l’encastrement sont une force verticale de 40 kN et un moment de 150 kNm.
- Le Diagramme des Moments Fléchissants (DMF) décroît linéairement de 150 kNm à 0 kNm de l’encastrement à l’extrémité libre.
- Le déplacement total à l’extrémité libre est d’environ 9.11 mm, ce qui est significativement plus élevé que le résultat initialement calculé de 2.60 mm.
Déplacement de l’Extrémité Libre
D’autres exercices de Rdm:




0 commentaires