Calcul des moments d’inertie
Comprendre le Calcul des moments d’inertie
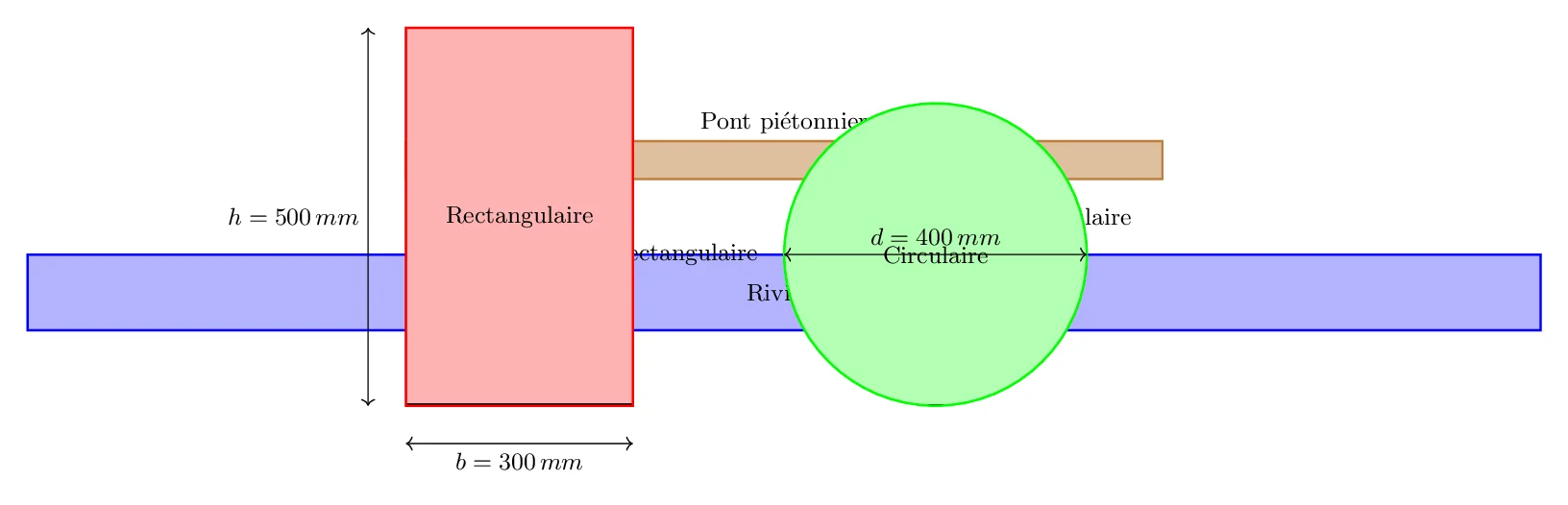
Un ingénieur civil est en train de concevoir un pont piétonnier au-dessus d’une rivière. Pour garantir la sécurité et la durabilité du pont, l’ingénieur doit choisir les matériaux appropriés et calculer les dimensions des poutres qui supporteront le pont. Les poutres seront disposées de manière à maximiser la résistance et minimiser le coût. Deux types de sections sont envisagés pour les poutres : rectangulaire et circulaire.
L’ingénieur doit calculer et comparer les moments d’inertie de ces deux types de sections pour déterminer laquelle offre la meilleure combinaison de résistance et d’efficacité matérielle.
Pour comprendre les Propriétés mécaniques des matériaux, cliquez sur le lien.
Données de l’exercice:
- Section Rectangulaire:
- Largeur (b) = 300 mm
- Hauteur (h) = 500 mm
- Section Circulaire:
- Diamètre (d) = 400 mm
Questions :
1. Calculer le moment d’inertie de la section rectangulaire.
2. Calculer le moment d’inertie de la section circulaire.
3. Comparer les résultats et discuter quelle section serait la plus avantageuse en termes de résistance pour les poutres du pont piétonnier.
Correction : Calcul des moments d’inertie
1. Calcul du moment d’inertie de la section rectangulaire
Le moment d’inertie d’une section rectangulaire, par rapport à un axe passant par son centre et parallèle à la largeur, se calcule à l’aide de la formule suivante. Ce paramètre est un indicateur de la résistance de la poutre en flexion : plus le moment d’inertie est élevé, meilleure est la capacité de la section à résister à la flexion.
Formule
Pour une section rectangulaire de largeur \(b\) et de hauteur \(h\) :
\[ I_{\text{rect}} = \frac{b \cdot h^3}{12} \]
Données
- \(b = 300\,\text{mm}\)
- \(h = 500\,\text{mm}\)
Calcul
1. Calcul de \(h^3\) :
\[ h^3 = 500^3 \] \[ = 500 \times 500 \times 500 \] \[ = 125\,000\,000\,\text{mm}^3 \]
2. Multiplication par \(b\) :
\[ b \cdot h^3 = 300 \times 125\,000\,000 \] \[ = 37\,500\,000\,000\,\text{mm}^4 \]
3. Division par 12 :
\[ I_{\text{rect}} = \frac{37\,500\,000\,000}{12} \] \[ I_{\text{rect}} \approx 3\,125\,000\,000\,\text{mm}^4 \]
Résultat : Le moment d’inertie de la section rectangulaire est d’environ \(3,125 \times 10^9\) mm\(^4\).
2. Calcul du moment d’inertie de la section circulaire
Pour une section circulaire, le moment d’inertie (aussi appelé « moment quadratique ») autour de son axe neutre se calcule en fonction du diamètre. Ce calcul permet d’évaluer la résistance de la section aux sollicitations en flexion.
Formule
Pour une section circulaire de diamètre \(d\) :
\[ I_{\text{circ}} = \frac{\pi \cdot d^4}{64} \]
Données
- \(d = 400\,\text{mm}\)
Calcul
1. Calcul de \(d^4\) :
\[ d^4 = 400^4 \] \[ = 400 \times 400 \times 400 \times 400 \] \[ = 25\,600\,000\,000\,\text{mm}^4 \]
2. Application de la formule :
\[ I_{\text{circ}} = \frac{\pi \cdot 25\,600\,000\,000}{64} \]
3. Simplification :
\[ \frac{25\,600\,000\,000}{64} = 400\,000\,000 \] \(\text{(car } 25\,600\,000\,000 \div 64 = 400\,000\,000\text{)} \)
Ainsi,
\[ I_{\text{circ}} = 400\,000\,000 \times \pi \] \[ I_{\text{circ}} \approx 400\,000\,000 \times 3,1416 \] \[ I_{\text{circ}} \approx 1\,256\,640\,000\,\text{mm}^4 \]
Résultat : Le moment d’inertie de la section circulaire est d’environ \(1,2566 \times 10^9\) mm\(^4\).
3. Comparaison et discussion
- Section Rectangulaire : \(I_{\text{rect}} \approx 3,125 \times 10^9\) mm\(^4\)
- Section Circulaire : \(I_{\text{circ}} \approx 1,2566 \times 10^9\) mm\(^4\)
Analyse :
- Le moment d’inertie de la section rectangulaire est significativement plus élevé que celui de la section circulaire pour les dimensions considérées.
- Avantage en résistance : Une valeur de moment d’inertie plus élevée indique une meilleure résistance à la flexion. Ainsi, la section rectangulaire, avec \(3,125 \times 10^9\) mm\(^4\), offrira une plus grande rigidité par rapport à la section circulaire.
- Considérations complémentaires : En dehors du simple calcul des moments d’inertie, il convient de prendre en compte d’autres facteurs tels que la distribution des matériaux, le coût, le poids et les conditions de mise en œuvre. Toutefois, sur le critère de la résistance à la flexion, la section rectangulaire semble être plus avantageuse pour la conception des poutres du pont piétonnier
Conclusion
L’ingénieur pourra ainsi conclure que, pour des dimensions équivalentes, la \textbf{section rectangulaire} offre un meilleur moment d’inertie (\(3,125 \times 10^9\) mm\(^4\)) comparé à la section circulaire (\(1,2566 \times 10^9\) mm\(^4\)), ce qui en fait un choix judicieux pour maximiser la résistance et la rigidité des poutres supportant le pont piétonnier.
Calcul des moments d’inertie
D’autres exercices de rdm:















Pas mal