Vérification de l’équilibre des forces verticales
Comprendre la Vérification de l’équilibre des forces verticales
Vous êtes ingénieur en structure et travaillez sur la conception d’un pont piétonnier. Ce pont est modélisé par une poutre complexe soutenue par deux appuis : un appui fixe (encastrement) à l’une de ses extrémités et un appui simple (rouleau) à l’autre extrémité.
La poutre est soumise à des charges réparties et concentrées dues au poids des passants et à l’installation d’éclairages le long du pont.
Pour comprendre le calcul de la Poutre encastrée et Diagramme des Moments, cliquez sur le lien.
Données:
- Longueur de la poutre, L, est de 20 m.
- Une charge uniformément répartie, q, de 5 kN/m sur toute la longueur de la poutre due au poids des passants.
- Une charge concentrée, P, de 30 kN à 5 m du support encastrement due à un élément d’éclairage.
- Le poids propre de la poutre est négligé.
- Le système est en équilibre statique.
Questions:
1. Dessiner le schéma de la poutre avec toutes les charges appliquées et les réactions d’appui.
2. Calculer les réactions aux appuis (notées RA pour l’encastrement et RB pour le rouleau).
3. Vérifier l’équilibre de la poutre en utilisant les équations d’équilibre : \(\sum F_x = 0\), \(\sum F_y = 0\), \(\sum M_A = 0\).
Correction : Vérification de l’équilibre des forces verticales
1. Dessin du schéma
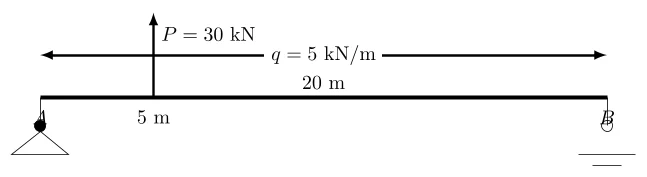
2. Calcul des réactions d’appui
Calcul de RB
Pour trouver RB, on utilise l’équilibre des moments autour de l’appui A. Le moment dû à la charge répartie est calculé en prenant le poids total de la charge répartie \((q \cdot L)\) multiplié par la distance de son centre de gravité à l’appui A \(\left(\frac{L}{2}\right)\).
Pour la charge concentrée P, le moment est P multiplié par sa distance à l’appui A (5 m).
\[ M_q = q \cdot L \cdot \frac{L}{2} \] \[ M_q = 5 \cdot 20 \cdot \frac{20}{2} \] \[ M_q = 1000 \, \text{kNm} \]
\[ M_P = P \cdot a \] \[ M_P = 30 \cdot 5 = 150 \, \text{kNm} \]
L’équation d’équilibre des moments autour de A donne :
\[ R_B \cdot L = M_q + M_P \] \[
R_B \cdot 20 = 1000 + 150 \] \[
R_B = \frac{1150}{20} = 57.5 \, \text{kN} \]
Calcul de RA
Pour trouver RA, on utilise l’équilibre des forces verticales :
\[ R_A + R_B = q \cdot L + P \] \[ R_A + 57.5 = 5 \cdot 20 + 30 \] \[ R_A = 100 + 30 – 57.5 \] \[ R_A = 72.5 \, \text{kN} \]
3. Vérification de l’équilibre
Vérification de l’équilibre des forces verticales :
\( R_A + R_B = 72.5 + 57.5 = 130 \, \text{kN} \)
La somme des charges sur la poutre est \(q \cdot L + P = 5 \cdot 20 + 30 = 130 \, \text{kN}\), ce qui confirme que l’équilibre des forces verticales est respecté.
Vérification de l’équilibre des moments autour de l’appui A :
Le moment total généré par les charges est \(1000 + 150 = 1150 \, \text{kNm}\), et le moment résistant dû aux réactions d’appui est \(R_B \cdot L = 57.5 \cdot 20 = 1150 \, \text{kNm}\). Cela confirme que l’équilibre des moments est aussi respecté.
Conclusion
Les réactions d’appui pour la poutre sous les charges données sont \(R_A = 72.5 \, \text{kN}\) (à l’encastrement) et \(R_B = 57.5 \, \text{kN}\) (au rouleau).
La vérification des conditions d’équilibre montre que ces valeurs assurent l’équilibre statique de la poutre, ce qui valide la correction de l’exercice.
Vérification de l’équilibre des forces verticales
D’autres exercices de Rdm:




0 commentaires