Méthode des Nœuds pour un Treillis

Comprendre la Méthode des Nœuds pour un Treillis

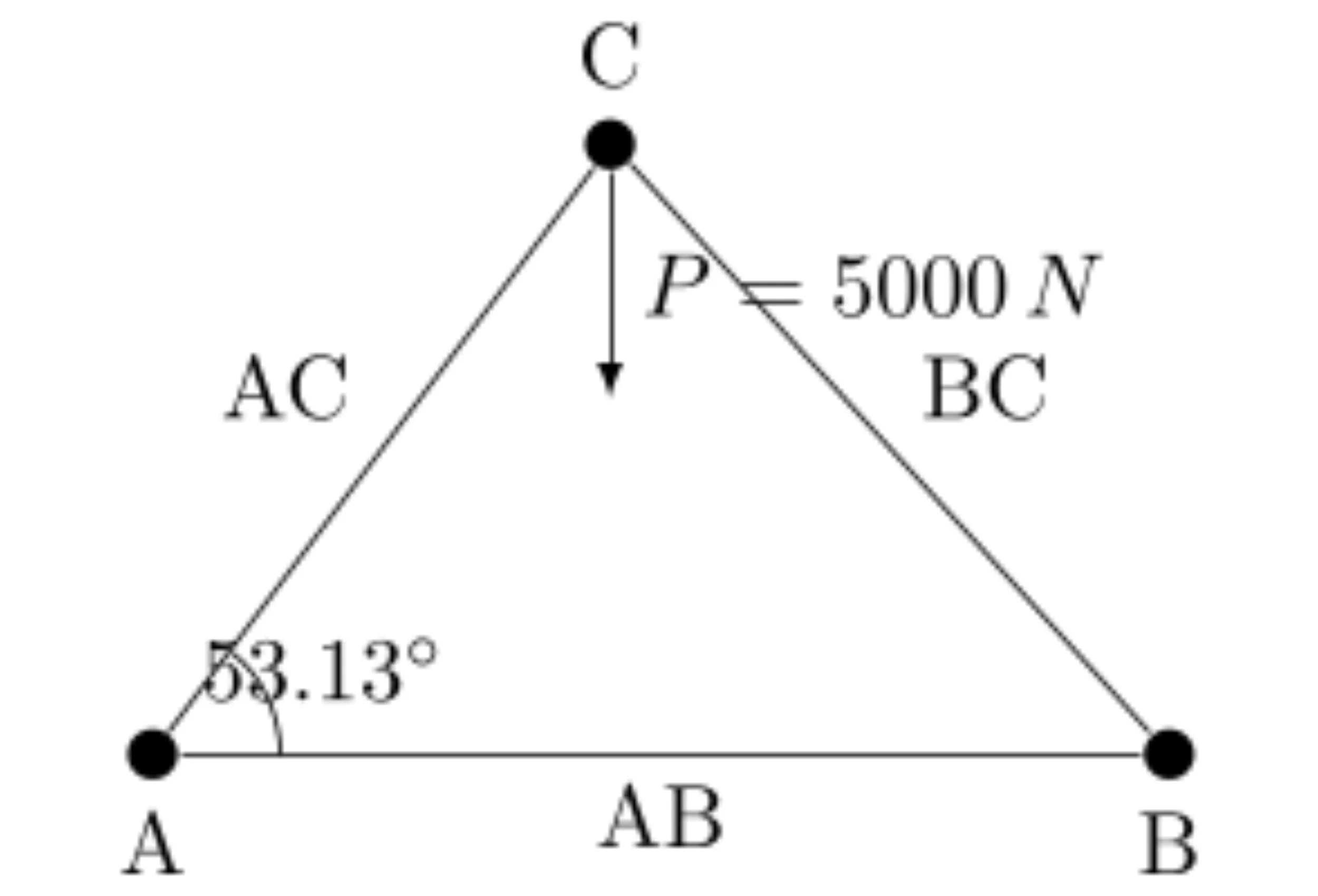
Considérons un treillis plan en forme de triangle, composé de trois nœuds et trois éléments (barres).

Le treillis est fixé au sol à l’un de ses nœuds (nœud A) et est supporté par un rouleau à un autre nœud (nœud B), permettant ainsi un mouvement vertical mais pas horizontal.

Le troisième nœud (nœud C) est libre et porte une charge verticale. Les longueurs des éléments du treillis sont également données.

• Nœuds: A (fixe), B (rouleau), C (libre avec charge)
• Charge appliquée au nœud C: P = 5000 N (verticalement vers le bas)
• Longueurs des éléments:
  • Barre AC = 3 m
  • Barre BC = 4 m
  • Barre AB = 5 m
• Angle entre la barre AC et l’horizontale = 53.13° (calculé à partir des longueurs données)

Objectif

Utiliser la méthode des nœuds pour déterminer les forces dans chaque barre du treillis.

Résolution

1. Calculer les réactions d’appui au nœud A \((A_x, A_y)\) et au nœud B \((B_y)\).
2. Analyser le nœud C en utilisant l’équilibre des forces \((ΣF_x = 0, ΣF_y = 0)\) pour trouver les forces dans les barres AC et BC.
3. Analyser le nœud A ou B en utilisant l’équilibre des forces pour trouver la force dans la barre AB.

Correction : Méthode des Nœuds pour un Treillis

1. Réactions d’Appui

1.1 Équilibre Vertical

• Nœud A est fixe, avec des réactions horizontale \( A_x \) et verticale \( A_y \).
• Nœud B est sur un rouleau, avec une réaction verticale uniquement, \( B_y \).

Équilibre vertical global (ΣF\(_y\) = 0):

\[ A_y + B_y = P = 5000 \, N \]

1.2 Équilibre des Moments autour de A

• Calcul de la distance horizontale \( L \) entre A et C:

\[ L = AC \times \cos(53.13^\circ) \] \[ L = 3 \times 0.6 \] \[ L \approx 1.8 \, m \]

• Équilibre des moments:

\[ P \times L = B_y \times 5 \, m \], donc \[ B_y = \frac{5000 \times 1.8}{5} \] \[ B_y = 1800 \, N \]

1.3 Calcul de \( A_y \)

En utilisant \[ A_y + B_y = 5000 \, N \] \[ A_y = 5000 – 1800 \] \[ A_y = 3200 \, N \]

2. Analyse du Nœud C

2.1 Équilibre Horizontal (ΣF\(_x\) = 0)

\[ F_{AC} \cdot \cos(53.13^\circ) = F_{BC} \]

2.2 Équilibre Vertical (ΣF\(_y\) = 0)

\[ F_{AC} \cdot \sin(53.13^\circ) = 5000 \, N \]

Résolution pour \( F_{AC} \) et \( F_{BC} \)

\[ F_{AC} = \frac{5000}{\sin(53.13^\circ)} \] \[ F_{AC} \approx 6250 \, N \] (en tension).

\[ F_{BC} = 6250 \cdot \cos(53.13^\circ) \] \[ F_{BC} \approx 3750 \, N \] (en tension).

3. Analyse du Nœud A ou B

3.1 Équilibre Horizontal (ΣF\(_x\) = 0)

\[ F_{AB} = F_{BC} = 3750 \, N \] (en tension)

3.2 Équilibre Vertical (ΣF\(_y\) = 0)

• Vérification :

\[ = 3200 \, N + 5000 \, N \] \[ = 8200 \, N \], ce qui équilibre la charge de 5000 N et la réaction de 3200 N sur A.

Résultat Final

• Force dans la barre AC (F\(_{AC}\)) = 6250 N (en tension).
• Force dans la barre BC (F\(_{BC}\)) = 3750 N (en tension).
• Force dans la barre AB (F\(_{AB}\)) = 3750 N (en tension).

Méthode des Nœuds pour un Treillis

D’autres exercices de Rdm:

• Calcul de la torsion d’un poteau
• Calcul des contraintes thermiques
• Calcul de l’Énergie de Déformation