Calcul de la torsion d’un poteau
Comprendre le Calcul de la torsion d’un poteau
Un ingénieur en génie civil doit concevoir un poteau de soutien pour un pont. Ce poteau doit être capable de résister à des moments de torsion générés par les forces du vent et les charges de trafic.
Pour comprendre la Torsion dans une Poutre en T, cliquez sur le lien.
Données :
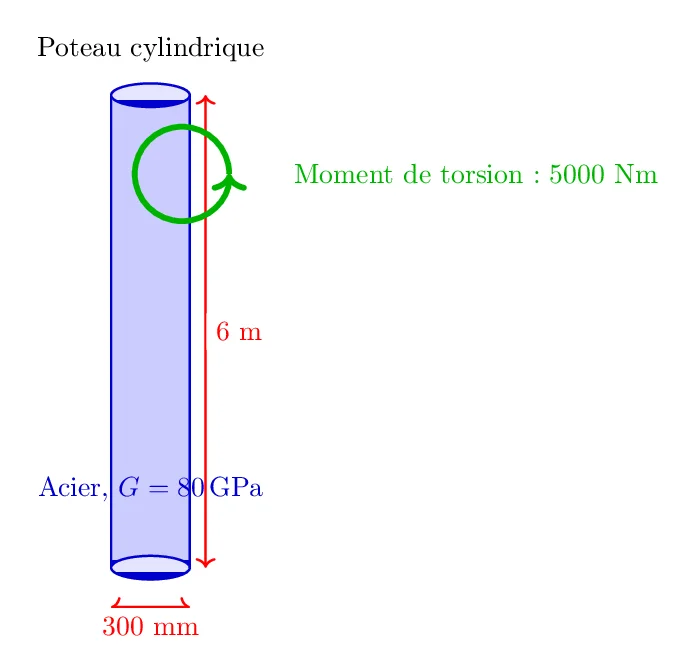
- Matériau du poteau : Acier (Module de rigidité G = 80 GPa)
- Forme du poteau : Cylindrique
- Diamètre du poteau : 300 mm
- Longueur du poteau : 6 m
- Moment de torsion appliqué : 5000 Nm
Questions :
1. Calcul de la contrainte de cisaillement maximale
2. Calcul de l’angle de torsion
3. Évaluation de la sécurité : En supposant une contrainte de cisaillement admissible de 120 MPa pour l’acier utilisé, évaluer si le poteau est sécuritaire sous la charge de torsion appliquée.
4. Discussion : Discuter de l’impact d’augmenter le diamètre du poteau sur la contrainte de cisaillement et l’angle de torsion.
Correction : Calcul de la torsion d’un poteau
1. Calcul de la contrainte de cisaillement maximale
Dans un poteau (ou arbre circulaire) soumis à un moment de torsion \(T\), la contrainte de cisaillement maximale se trouve à la surface et se calcule en fonction du rayon extérieur \(c\) et du moment polaire d’inertie \(J\) de la section. Pour une section circulaire, la formule simplifiée est :
Formule
\[ \tau_{\text{max}} = \frac{T \times c}{J} \quad \text{avec} \quad c = \frac{d}{2} \] et \[ J = \frac{\pi d^4}{32} \]
En remplaçant \(c\) dans la formule, on obtient :
\[ \tau_{\text{max}} = \frac{T \times \frac{d}{2}}{\frac{\pi d^4}{32}} = \frac{16T}{\pi d^3} \]
Données
- Moment de torsion appliqué : \(T = 5000 \, \text{Nm}\)
- Diamètre du poteau : \(d = 300 \, \text{mm} = 0,3 \, \text{m}\)
Calcul
1. Calcul de \(d^3\) :
\[ d^3 = (0,3)^3 = 0,027 \, \text{m}^3 \]
2. Substitution dans la formule :
\[ \tau_{\text{max}} = \frac{16 \times 5000}{\pi \times 0,027} \]
2. Calcul numérique :
\[ \tau_{\text{max}} = \frac{80000}{0,084823} \approx 942477,8 \, \text{Pa} \]
3. Conversion en MPa :
\[ 942477,8 \, \text{Pa} = 0,9425 \, \text{MPa} \]
2. Calcul de l’angle de torsion
L’angle de torsion \(\theta\) (en radians) d’un poteau soumis à un moment de torsion se calcule à l’aide de la formule suivante. Ce calcul intègre la longueur \(L\), le moment polaire d’inertie \(J\) et le module de rigidité \(G\) du matériau.
Formule
\[ \theta = \frac{T \times L}{J \times G} \]
Données
- Moment de torsion appliqué : \(T = 5000 \, \text{Nm}\)
- Longueur du poteau : \(L = 6 \, \text{m}\)
- Diamètre du poteau : \(d = 0,3 \, \text{m}\)
- Module de rigidité de l’acier : \(G = 80 \, \text{GPa} = 80 \times 10^9 \, \text{Pa}\)
Calcul du moment polaire d’inertie \(J\) pour une section circulaire :
\[ J = \frac{\pi d^4}{32} \]
Calculons \(d^4\) :
\[ d^4 = (0,3)^4 = 0,0081 \, \text{m}^4 \]
Puis :
\[ J = \frac{\pi \times 0,0081}{32} \] \[ J \approx \frac{0,025447}{32} \] \[ J \approx 0,00079522 \, \text{m}^4 \]
Calcul
1. Substitution dans la formule de \(\theta\) :
\[ \theta = \frac{5000 \times 6}{0,00079522 \times 80 \times 10^9} \] \[ \theta \approx \frac{30000}{63617600} \] \[ \theta \approx 0,000471 \, \text{rad} \]
3. Évaluation de la sécurité
Données de sécurité
- Contrainte de cisaillement admissible pour l’acier : \(\tau_{\text{adm}} = 120 \, \text{MPa}\)
Comparaison
La contrainte de cisaillement maximale calculée est de :
\[ \tau_{\text{max}} \approx 0,9425 \, \text{MPa} \]
Comparée à la contrainte admissible de \(120 \, \text{MPa}\), nous avons :
\[ 0,9425 \, \text{MPa} \ll 120 \, \text{MPa} \]
Conclusion : Le poteau est donc très sécuritaire sous la charge de torsion appliquée.
4. Discussion : Impact de l’augmentation du diamètre du poteau
Effet sur la contrainte de cisaillement maximale
La formule :
\[ \tau_{\text{max}} = \frac{16T}{\pi d^3} \]
montre que la contrainte de cisaillement est inversement proportionnelle au cube du diamètre \(d\).
Augmentation du diamètre :
- Augmenter \(d\) augmente \(d^3\) de manière exponentielle.
- Cela entraîne une réduction significative de \(\tau_{\text{max}}\).
Effet sur l’angle de torsion
La formule :
\[ \theta = \frac{T \times L}{J \times G} \quad \text{avec} \quad J = \frac{\pi d^4}{32} \]
montre que l’angle de torsion est inversement proportionnel à \(d^4\).
Augmentation du diamètre :
- Une augmentation de \(d\) augmente \(d^4\) encore plus fortement.
- Cela se traduit par une diminution très marquée de l’angle de torsion.
Synthèse
- Contrainte de cisaillement : Un diamètre plus grand réduit la contrainte, améliorant ainsi la résistance du poteau.
- Angle de torsion : Un diamètre accru diminue l’angle de torsion, améliorant la rigidité torsionnelle.
Calcul de la torsion d’un poteau
D’autres exercices de Rdm:















0 commentaires