Calcul du Module d’Élasticité d’une Poutre
Comprendre le Calcul du Module d’Élasticité d’une Poutre
Vous êtes ingénieur(e) dans une entreprise spécialisée dans la conception de structures métalliques. Un nouveau projet nécessite la conception d’une poutre en acier qui supportera une charge uniformément répartie. Pour garantir la sécurité et l’efficacité de la conception, vous devez calculer le module d’élasticité de l’acier utilisé, afin de vérifier sa conformité avec les spécifications du projet.
Pour comprendre le Calcul d’une poutre en acier, cliquez sur le lien.
Données:
- Matériau de la poutre: acier
- Longueur de la poutre (L): 3 mètres
- Charge uniformément répartie (q): 2000 N/m
- Flèche maximale admissible (f_max): 10 mm
- Moment d’inertie de la section transversale de la poutre (I): \(4 \times 10^{-6} m^4\)
- Distance entre les appuis (a): 3 mètres
Questions:
1. Calculer la réaction aux appuis
2. Déterminer le moment fléchissant maximal (\(M_{\text{max}}\))
3. Calculer le module d’élasticité (\(E\))
Correction : Calcul du Module d’Élasticité d’une Poutre
1. Calcul des réactions aux appuis
Pour une charge uniformément répartie, la réaction aux appuis est égale à la moitié de la charge totale appliquée à la poutre. La charge totale Q est le produit de la charge par unité de longueur q et la longueur de la poutre L.
\[Q = q \times L\]
La réaction aux appuis est donc donnée par:
\[R = \frac{Q}{2} = \frac{q \times L}{2}\]
En substituant les valeurs données :
- \(q = 2000\, \text{N/m}\)
- \(L = 3\, \text{m}\)
\[R = \frac{2000 \times 3}{2} \] \[R = 3000\, \text{N}\]
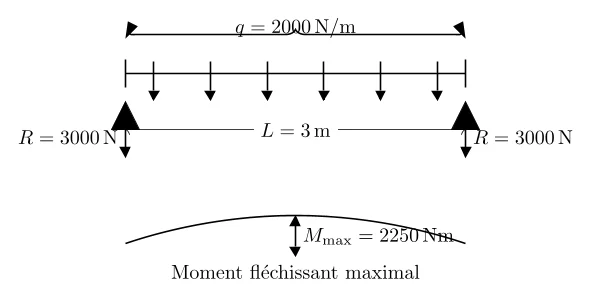
Chaque appui supporte une réaction de 3000 N.
2. Détermination du moment fléchissant maximal (\(M_{\text{max}}\))
Le moment fléchissant maximal pour une poutre supportant une charge uniformément répartie se produit au centre de la poutre.
\[M_{\text{max}} = \frac{q \times L^2}{8}\]
En substituant les valeurs données :
\[M_{\text{max}} = \frac{2000 \times (3)^2}{8} \] \[M_{\text{max}} = \frac{2000 \times 9}{8} \] \[M_{\text{max}} = 2250\, \text{Nm}\]
3. Calcul du module d’élasticité (\(E\))
Le module d’élasticité est calculé en réarrangeant la formule de la flèche pour une charge uniformément répartie et en résolvant pour \(E\).
\[f = \frac{5 \times q \times L^4}{384 \times E \times I}\]
En réarrangeant pour \(E\) :
\[E = \frac{5 \times q \times L^4}{384 \times f \times I}\]
Substituons les valeurs fournies :
- \(f_{\text{max}} = 10\, \text{mm} = 0.01\, \text{m}\) (conversion en mètres pour garder la cohérence des unités)
- \(I = 4 \times 10^{-6}\, \text{m}^4\)
\[E = \frac{5 \times 2000 \times (3)^4}{384 \times 0.01 \times 4 \times 10^{-6}}\]
Calculons ce résultat :
\[E = \frac{5 \times 2000 \times 81}{384 \times 0.01 \times 4 \times 10^{-6}}\] \[E = \frac{810000}{0.01536}\] \[E = \frac{810000}{0.01536 \times 4 \times 10^{-6}}\] \[E = \frac{810000}{0.00006144}\] \[E = 13183673469.1\, \text{Pa}\] \[E \approx 132\, \text{GPa}\]
Ainsi, le module d’élasticité \(E\) de l’acier utilisé pour cette poutre est d’environ 132 GPa.
Calcul du Module d’Élasticité d’une Poutre
D’autres exercices de Rdm:
0 commentaires