Calcul des réactions d’appui
Comprendre le calcul des réactions d’appui
Vous êtes un ingénieur chargé de concevoir un pont pour une nouvelle route. Le pont doit être capable de supporter une charge uniformément répartie ainsi que des charges concentrées dues à des véhicules.
Pour comprendre le Calcul l’effort tranchant et le moment, cliquez sur le lien.
Données :
- Longueur du pont (L) : 20 mètres
- Charge uniformément répartie (q) : 5 kN/m
- Charge concentrée (P) : 30 kN, située à 5 mètres de l’appui gauche
- Le pont est supporté par deux appuis simples (A et B) situés respectivement à l’extrémité gauche et à l’extrémité droite du pont.
Objectif : Calculer les réactions d’appui aux points A et B.
Questions :
- Représentez schématiquement le pont avec ses charges.
- Utilisez l’équilibre statique pour établir les équations d’équilibre (somme des forces verticales = 0, somme des moments = 0).
- Calculez la réaction d’appui en A \((R_A)\) et en B \((R_B)\).
Correction : calcul des réactions d’appui
1. Représentation schématique du pont avec ses charges :
- Un pont de 20 mètres de long.
- Une charge uniformément répartie de 5 kN/m sur toute la longueur.
- Une charge concentrée de 30 kN, située à 5 mètres de l’appui gauche.
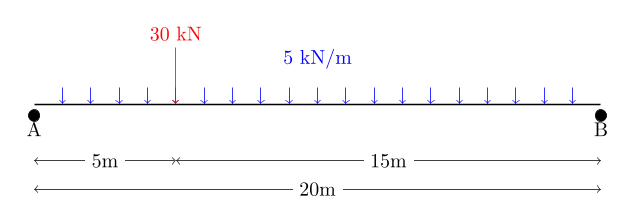
2. Équilibre statique pour établir les équations d’équilibre :
- Somme des forces verticales \((ΣFy = 0)\) : Les réactions aux appuis \((R_A et R_B)\) doivent équilibrer la charge totale.
- Somme des moments \((ΣM = 0)\) : Choisissons un point de pivot pour équilibrer les moments.
3. Calcul des réactions d’appui
Étape A – Calcul de la charge totale due à la charge uniformément répartie :
- Charge totale uniforme
\[ = q \times L = 5 \, \text{kN/m} \times 20 \, \text{m} \] \[ = 100 \, \text{kN} \]
Étape B – Application de la condition d’équilibre des forces verticales :
- \(\Sigma F_y = 0 \Rightarrow R_A + R_B = \text{Charge totale uniforme} + \text{Charge concentrée}\)
- \(R_A + R_B = 100 \, \text{kN} + 30 \, \text{kN} = 130 \, \text{kN}\)
Étape C – Application de la condition d’équilibre des moments :
- Choisissons l’appui A comme point de pivot.
\[\Sigma M_A = 0 \Rightarrow R_B \times L\] \[ = \left(\text{Charge totale uniforme} \times \frac{L}{2}\right) + \left(\text{Charge concentrée} \times \text{distance de l’appui A}\right)\] \[ R_B \times 20 \, \text{m} = \left(100 \, \text{kN} \times 10 \, \text{m}\right) + \left(30 \, \text{kN} \times 5 \, \text{m}\right)\]
\[ R_B \times 20 \, \text{m} = 1000 \, \text{kNm} + 150 \, \text{kNm} \] \[ R_B \times 20 \, \text{m} = 1150 \, \text{kNm} \] \[ R_B = \frac{1150 \, \text{kNm}}{20 \, \text{m}} = 57.5 \, \text{kN} \]
Étape D – Calcul de R_A en utilisant l’équation des forces verticales :
\[ R_A = 130 \, \text{kN} – R_B \] \[ R_A = 130 \, \text{kN} – 57.5 \, \text{kN} \] \[ R_A = 72.5 \, \text{kN} \]
Résumé :
- Réaction d’appui en A (\(R_A\)) = 72.5 kN.
- Réaction d’appui en B (\(R_B\)) = 57.5 kN.
Ces calculs démontrent l’importance d’appliquer correctement les principes de l’équilibre statique pour résoudre les problèmes en RDM.
Ils montrent également comment les forces distribuées et concentrées influencent les réactions aux appuis dans les structures.
Calcul des réactions d’appui
D’autres exercices de Rdm:




Vraiment merci pour l’explication approfondie sur le calcul des réactions d’appuis.