Cisaillement dans une poutre
Comprendre le cisaillement dans une poutre
Vous êtes ingénieur en structure et vous devez analyser une poutre en acier simplement appuyée qui supporte une charge uniformément répartie ainsi que des charges concentrées.
L’objectif est de déterminer la contrainte de cisaillement maximale dans la poutre.
Pour comprendre la Déformation Axiale Due à la Température, cliquez sur le lien.
Données de l’Exercice
- Longueur de la poutre, \( L = 6 \) mètres
- Charge uniformément répartie, \( w = 5 \) kN/m
- Charges concentrées : \( P_1 = 10 \) kN à 2 m du support gauche, \( P_2 = 15 \) kN à 4 m du support gauche
- Largeur de la section transversale de la poutre, \( b = 150 \) mm
- Hauteur de la section transversale de la poutre, \( h = 300 \) mm
- La poutre est en acier avec une limite d’élasticité de 250 MPa
Questions:
1. Calcul des Réactions aux Appuis :
- Déterminez les réactions aux appuis en considérant les charges appliquées.
2. Diagramme de Cisaillement :
- Construisez le diagramme de cisaillement de la poutre. Identifiez les points où le cisaillement est maximal.
3. Calcul de la Contrainte de Cisaillement :
- Utilisez la formule de cisaillement, \(\tau = \frac{VQ}{Ib}\), où \( V \) est la force de cisaillement, \( Q \) est le moment statique de la zone au-dessus du point d’intérêt, \( I \) est le moment d’inertie de la section transversale, et \( b \) est la largeur de la poutre. Calculez la contrainte de cisaillement maximale dans la poutre.
4. Vérification de la Sécurité :
- Comparez la contrainte de cisaillement maximale trouvée avec la limite d’élasticité de l’acier.
- Vérifiez si la poutre est sûre pour les charges données.
Correction : cisaillement dans une poutre
1. Calcul des Réactions aux Appuis
Étape 1: Équilibre vertical
\[R_A + R_B = wL + P_1 + P_2\]
\[ = (5\,\text{kN/m} \times 6\,\text{m}) + 10\,\text{kN} + 15\,\text{kN} \] \[ = 30\,\text{kN} + 25\,\text{kN} \] \[ = 55\,\text{kN} \]
Étape 2: Moment autour d’un des appuis (disons autour de A)
\[R_B \times L = w \times \frac{L}{2} \times L + P_1 \times 2\,\text{m} + P_2 \times 4\,\text{m}\] \[R_B \times 6\,\text{m} = 5\,\text{kN/m} \times 3\,\text{m} \times 6\,\text{m} + 10\,\text{kN} \times 2\,\text{m} + 15\,\text{kN} \times 4\,\text{m}\] \[R_B = \frac{90 + 20 + 60}{6}\,\text{kN}\] \[R_B = \frac{170}{6}\,\text{kN}\] \[R_B \approx 28.33\,\text{kN}\]
Réaction à A:
\[R_A = 55\,\text{kN} – 28.33\,\text{kN} = 26.67\,\text{kN}\]
2. Diagramme de Cisaillement de la Poutre
De 0 à 2 m (Entre l’appui A et la charge \(P_1\)
- Au point A (0 m), le cisaillement commence à \(V = R_A = 26.67\, \text{kN}\).
- À une distance \(x\) (où \(0 < x < 2\, \text{m}\)) de l’appui A, la charge répartie qui a agi jusqu’à ce point est \(w \times x = 5\, \text{kN/m} \times x\).
- Le cisaillement à ce point est donc
\[ V(x) = R_A – w \times x \]\[ V(x) = 26.67\, \text{kN} – 5\, \text{kN/m} \times x.\]
À 2 m, avant l’application de \(P_1\), le cisaillement sera
\[ V(2) = 26.67\, \text{kN} – 5\, \text{kN/m} \times 2\, \text{m} \] \[ V(2) = 26.67\, \text{kN} – 10\, \text{kN} \] \[ V(2) = 16.67\, \text{kN}.
\]
À 2 m (Effet de la charge \(P_1\))
Juste après l’application de la charge \(P_1\), le cisaillement chute de 10 kN. Donc, à 2 m, juste après \(P_1\), le cisaillement est de
\[ = 16.67\, \text{kN} – 10\, \text{kN} = 6.67\, \text{kN}.
\]
De 2 m à 4 m
De la même manière, entre 2 m et 4 m, le cisaillement continue de diminuer linéairement à cause de la charge répartie. À 4 m, avant \(P_2\), il sera
\[ = 6.67\, \text{kN} – 5\, \text{kN/m} \times 2\, \text{m} \] \[ = 6.67\, \text{kN} – 10\, \text{kN} = -3.33\, \text{kN} \]
À 4 m (Effet de la charge \(P_2\))
Juste après l’application de la charge \(P_2\), le cisaillement chute de 15 kN. Donc, à 4 m, juste après \(P_2\), le cisaillement est de
\[ = -3.33\, \text{kN} – 15\, \text{kN} \] \[ = -18.33\, \text{kN} \]
De 4 m à 6 m
Entre 4 m et 6 m, le cisaillement continue de diminuer linéairement jusqu’à l’appui B. À l’appui B (6 m), le cisaillement est
\[ = -18.33\, \text{kN} – 5\, \text{kN/m} \times 2\, \text{m} \] \[ = -18.33\, \text{kN} – 10\, \text{kN} \] \[ = -28.33\, \text{kN}, \]
ce qui correspond à la réaction en B.
Résumé et Implications pour le Diagramme de Cisaillement
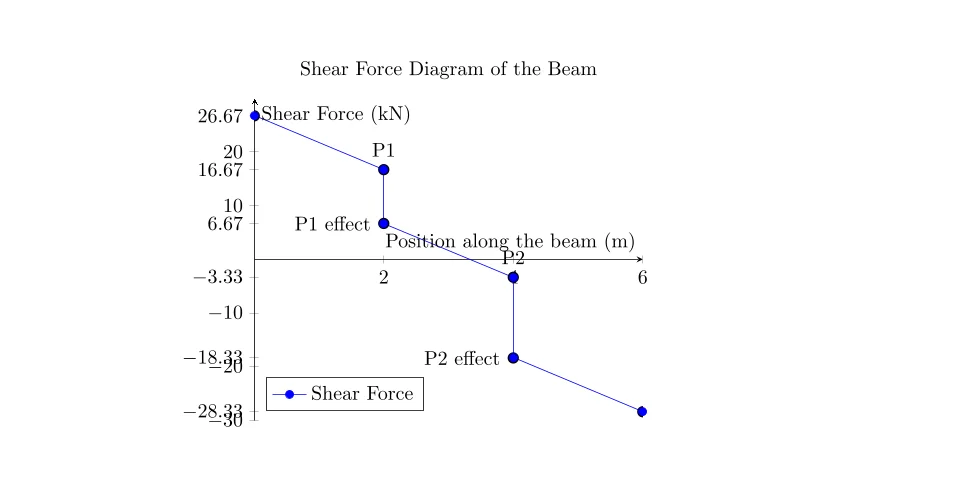
Le diagramme commence à \(+26.67\, \text{kN}\) à l’appui A, descend linéairement jusqu’à \(+16.67\, \text{kN}\) à 2 m, puis chute brusquement à \(+6.67\, \text{kN}\).
Il continue de descendre linéairement jusqu’à \(-3.33\, \text{kN}\) à 4 m, puis chute brusquement à \(-18.33\, \text{kN}\). Finalement, il continue à descendre linéairement jusqu’à \(-28.33\, \text{kN}\) à l’appui B.
3. Calcul de la Contrainte de Cisaillement
Moment d’inertie (I) de la section transversale rectangulaire:
\begin{align*}
I &= \frac{bh^3}{12} \end{align*} \begin{align*}
I & = \frac{0.15 \, \text{m} \times (0.3 \, \text{m})^3}{12} \end{align*} \begin{align*}
I & \approx 0.0003375 \, \text{m}^4
\end{align*}
Moment statique (Q) pour la hauteur maximale (au centre de la poutre):
\begin{align*}
Q &= A’ \times y’ \end{align*} \begin{align*}
Q & = \frac{bh}{2} \times \frac{h}{4} \end{align*} \begin{align*}
Q & = \frac{0.15 \, \text{m} \times 0.3 \, \text{m}}{2} \times \frac{0.3 \, \text{m}}{4} \end{align*} \begin{align*}
Q & \approx 0.003375 \, \text{m}^3
\end{align*}
Contrainte de cisaillement maximale (\(\tau_{\text{max}}\)) au point de cisaillement maximal (par exemple, à l’appui A):
\begin{align*}
\tau_{\text{max}} &= \frac{V_{\text{max}} Q}{Ib} \end{align*}
\[ \tau_{\text{max}} = \frac{26.67 \times 10^3 \, \text{N} \times 0.003375 \, \text{m}^3}{0.0003375 \, \text{m}^4 \times 0.15 \, \text{m}} \] \begin{align*}
\tau_{\text{max}} & \approx 1.67 \, \text{MPa}
\end{align*}
4. Vérification de la Sécurité
La contrainte de cisaillement maximale est \(\tau_{\text{max}} = 1.67 \, \text{MPa}\), qui est bien inférieure à la limite d’élasticité de l’acier de 250 MPa.
Par conséquent, la poutre est considérée comme sûre sous ces charges.
Cisaillement dans une poutre
D’autres exercices de Rdm :




0 commentaires