Études de cas pratique

EGC

Calcul des déformations dans une poutre

Calcul des Déformations dans une Poutre

Comprendre les Déformations des Poutres

Lorsqu'une poutre est soumise à des charges, elle se déforme. La ligne joignant les centres de gravité des sections droites de la poutre déformée est appelée la **déformée** ou **ligne élastique**. La distance verticale entre la position initiale d'un point sur l'axe neutre et sa position sur la déformée est appelée la **flèche** (\(y(x)\) ou \(v(x)\)). La pente de la déformée en un point est appelée la **rotation** (\(\theta(x)\) ou \(y'(x)\)).

Le calcul des déformations est essentiel pour vérifier que la poutre respecte les critères de service (limitation des flèches pour le confort, l'aspect, ou le bon fonctionnement d'éléments supportés) et pour des analyses plus avancées (structures hyperstatiques). La méthode de la double intégration de l'équation du moment fléchissant est une approche courante : \(EI y'' = M(x)\).

Cet exercice se concentre sur une poutre sur appuis simples avec une charge ponctuelle en son milieu.

Données de l'étude

Une poutre AB, de longueur \(L\), repose sur un appui simple (articulé) en A (\(x=0\)) et un appui à rouleau en B (\(x=L\)). Elle est soumise à une charge ponctuelle \(P\) appliquée verticalement vers le bas au milieu de sa portée (\(x=L/2\)). La poutre a une rigidité flexionnelle \(EI\) constante.

Caractéristiques :

  • Longueur de la poutre (\(L\)) : \(5 \, \text{m}\)
  • Charge ponctuelle (\(P\)) : \(20 \, \text{kN}\)
  • Rigidité flexionnelle (\(EI\)) : \(30 \times 10^3 \, \text{kN} \cdot \text{m}^2\) (Note: \(E\) est le module d'Young, \(I\) le moment d'inertie de la section).
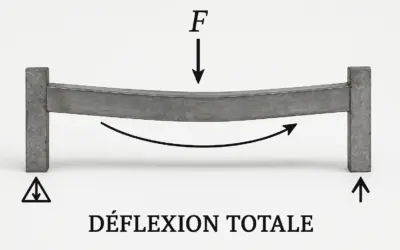
Schéma de la Poutre et de sa Déformée
{/* */} A B C (L/2) {/* */} {/* */} Rₐ Rₑ {/* */} P {/* */} y_max θₐ θₑ {/* */} L = 5 m L/2 {/* */} x 0

Poutre sur appuis simples avec charge ponctuelle P au milieu et sa déformée schématique.

Questions à traiter

  1. Calculer les réactions d'appui en A (\(R_A\)) et en B (\(R_B\)).
  2. Établir l'équation du moment fléchissant \(M(x)\) pour la section \(0 \le x \le L/2\). (Par symétrie, l'analyse de la moitié de la poutre suffit pour la déformée).
  3. En utilisant l'équation différentielle de la déformée \(EI \frac{d^2y}{dx^2} = M(x)\), intégrer deux fois pour obtenir l'équation de la rotation \(\theta(x) = y'(x)\) et l'équation de la flèche \(y(x)\) pour \(0 \le x \le L/2\).
  4. Déterminer les constantes d'intégration en utilisant les conditions aux limites appropriées.
  5. Calculer la flèche maximale (\(y_{max}\)) et indiquer sa position.
  6. Calculer la rotation (ou pente) aux appuis A (\(\theta_A\)) et B (\(\theta_B\)).

Correction : Calcul des Déformations dans une Poutre

Question 1 : Réactions d'appui

Principe :

En raison de la symétrie du chargement et des appuis, les réactions verticales en A et B sont égales et valent chacune la moitié de la charge totale appliquée.

Formule(s) utilisée(s) :
\[ \sum F_y = 0 \Rightarrow R_A + R_B - P = 0 \] \[ \sum M_A = 0 \Rightarrow R_B \cdot L - P \cdot \frac{L}{2} = 0 \]
Données spécifiques :
  • Charge \(P = 20 \, \text{kN}\)
  • Longueur \(L = 5 \, \text{m}\)
Calcul :
\[ \begin{aligned} R_B \cdot L &= P \cdot \frac{L}{2} \\ R_B &= \frac{P}{2} = \frac{20 \, \text{kN}}{2} = 10 \, \text{kN} \end{aligned} \]
\[ \begin{aligned} R_A + R_B &= P \\ R_A + 10 \, \text{kN} &= 20 \, \text{kN} \\ R_A &= 10 \, \text{kN} \end{aligned} \]
Résultat Question 1 :
Réaction d'appui en A : \(R_A = 10 \, \text{kN}\).
Réaction d'appui en B : \(R_B = 10 \, \text{kN}\).

Question 2 : Équation du moment fléchissant \(M(x)\) pour \(0 \le x \le L/2\)

Principe :

On effectue une coupure à une abscisse \(x\) dans l'intervalle \(0 \le x \le L/2\) et on considère l'équilibre en moments de la section de gauche. Convention : \(M(x)\) est positif s'il tend la fibre inférieure (sagging).

Calcul pour \(0 \le x \le L/2\) :
\[ M(x) = R_A \cdot x = 10x \quad (\text{kN.m, si x est en mètres}) \]
Résultat Question 2 : Pour \(0 \le x \le 2.5 \, \text{m}\), l'équation du moment fléchissant est \(M(x) = 10x \, \text{kN.m}\).

Question 3 : Intégration de l'équation de la déformée

Principe :

On utilise l'équation \(EI y'' = M(x)\). Une première intégration donne \(EI y' = EI \theta(x)\) (rotation) et une seconde intégration donne \(EI y(x)\) (flèche).

Calcul pour \(0 \le x \le L/2\) :
\[ EI \frac{d^2y}{dx^2} = 10x \]

Première intégration (rotation) :

\[ \begin{aligned} EI \frac{dy}{dx} &= \int 10x \, dx \\ EI y' &= \frac{10x^2}{2} + C_1 \\ EI y' &= 5x^2 + C_1 \end{aligned} \]

Seconde intégration (flèche) :

\[ \begin{aligned} EI y &= \int (5x^2 + C_1) \, dx \\ EI y &= \frac{5x^3}{3} + C_1 x + C_2 \end{aligned} \]
Résultat Question 3 :
Équation de la rotation (multipliée par EI) : \(EI y'(x) = 5x^2 + C_1\).
Équation de la flèche (multipliée par EI) : \(EI y(x) = \frac{5x^3}{3} + C_1 x + C_2\).

Question 4 : Détermination des constantes d'intégration

Principe :

On utilise les conditions aux limites :
1. En \(x=0\) (appui A), la flèche est nulle : \(y(0) = 0\).
2. En \(x=L/2\) (milieu de la poutre), par symétrie, la rotation (pente de la déformée) est nulle : \(y'(L/2) = 0\).

Calcul des constantes :

Condition 1 : \(y(0) = 0\)

\[ \begin{aligned} EI y(0) &= \frac{5(0)^3}{3} + C_1 (0) + C_2 \\ 0 &= 0 + 0 + C_2 \\ C_2 &= 0 \end{aligned} \]

Condition 2 : \(y'(L/2) = 0\), avec \(L/2 = 2.5 \, \text{m}\)

\[ \begin{aligned} EI y'(L/2) &= 5(L/2)^2 + C_1 \\ 0 &= 5(2.5)^2 + C_1 \\ 0 &= 5(6.25) + C_1 \\ 0 &= 31.25 + C_1 \\ C_1 &= -31.25 \end{aligned} \]

Les unités pour \(C_1\) sont \(\text{kN} \cdot \text{m}^2\) et pour \(C_2\) sont \(\text{kN} \cdot \text{m}^3\), si \(x\) est en m, \(P\) en kN, et \(EI\) en \(\text{kN} \cdot \text{m}^2\).

Résultat Question 4 : Les constantes d'intégration sont :
\(C_1 = -31.25 \, \text{kN} \cdot \text{m}^2\).
\(C_2 = 0 \, \text{kN} \cdot \text{m}^3\).

Donc, pour \(0 \le x \le L/2\) :
\(EI y'(x) = 5x^2 - 31.25\).
\(EI y(x) = \frac{5x^3}{3} - 31.25x\).

Question 5 : Flèche maximale (\(y_{max}\))

Principe :

Par symétrie, la flèche maximale se produit au milieu de la poutre, à \(x = L/2 = 2.5 \, \text{m}\).

Calcul :
\[ \begin{aligned} EI y_{max} &= EI y(L/2) \\ &= \frac{5(L/2)^3}{3} - 31.25(L/2) \\ &= \frac{5(2.5)^3}{3} - 31.25(2.5) \\ &= \frac{5 \times 15.625}{3} - 78.125 \\ &= \frac{78.125}{3} - 78.125 \\ &= 26.04166... - 78.125 \\ &= -52.08333... \, \text{kN} \cdot \text{m}^3 \end{aligned} \]

La flèche \(y_{max}\) est donc :

\[ \begin{aligned} y_{max} &= \frac{-52.08333 \, \text{kN} \cdot \text{m}^3}{EI} \\ &= \frac{-52.08333 \, \text{kN} \cdot \text{m}^3}{30 \times 10^3 \, \text{kN} \cdot \text{m}^2} \\ &\approx -0.001736 \, \text{m} \\ &\approx -1.736 \, \text{mm} \end{aligned} \]

Le signe négatif indique que la flèche est vers le bas, ce qui est attendu. La valeur absolue de la flèche maximale est \(1.736 \, \text{mm}\). La formule classique pour ce cas est \(y_{max} = -\frac{PL^3}{48EI}\).

\[ \begin{aligned} y_{max} &= -\frac{20 \text{ kN} \times (5 \text{ m})^3}{48 \times 30000 \text{ kN.m}^2} \\ &= -\frac{20 \times 125}{48 \times 30000} \, \text{m} \\ &= -\frac{2500}{1440000} \, \text{m} \\ &= -\frac{25}{14400} \, \text{m} \approx -0.0017361 \, \text{m} \end{aligned} \]

Nos calculs correspondent. \(52.08333... = \frac{PL^3}{48} = \frac{20 \times 5^3}{48} = \frac{2500}{48} = \frac{625}{12}\).

Résultat Question 5 : La flèche maximale est \(y_{max} \approx -1.736 \, \text{mm}\) (vers le bas), située à \(x = L/2 = 2.5 \, \text{m}\).

Question 6 : Rotations aux appuis (\(\theta_A\) et \(\theta_B\))

Principe :

La rotation en A (\(\theta_A\)) est \(y'(0)\). Par symétrie, \(\theta_B = - \theta_A\).

Calcul :

Rotation en A (\(x=0\)) :

\[ \begin{aligned} EI y'(0) &= 5(0)^2 - 31.25 \\ EI \theta_A &= -31.25 \, \text{kN} \cdot \text{m}^2 \\ \theta_A &= \frac{-31.25 \, \text{kN} \cdot \text{m}^2}{EI} \\ &= \frac{-31.25 \, \text{kN} \cdot \text{m}^2}{30 \times 10^3 \, \text{kN} \cdot \text{m}^2} \\ &\approx -0.00104167 \, \text{rad} \end{aligned} \]

Rotation en B (\(x=L\)) : Par symétrie, \(\theta_B = -\theta_A\).

\[ \theta_B \approx +0.00104167 \, \text{rad} \]

La formule classique pour ce cas est \(\theta_A = -\frac{PL^2}{16EI}\) et \(\theta_B = \frac{PL^2}{16EI}\).

\[ \begin{aligned} \theta_A &= -\frac{20 \text{ kN} \times (5 \text{ m})^2}{16 \times 30000 \text{ kN.m}^2} \\ &= -\frac{20 \times 25}{16 \times 30000} \\ &= -\frac{500}{480000} = -\frac{5}{4800} \approx -0.00104167 \, \text{rad} \end{aligned} \]

Nos calculs correspondent. \(31.25 = \frac{PL^2}{16} = \frac{20 \times 5^2}{16} = \frac{500}{16}\).

Résultat Question 6 :
Rotation en A : \(\theta_A \approx -0.001042 \, \text{rad}\) (sens horaire).
Rotation en B : \(\theta_B \approx +0.001042 \, \text{rad}\) (sens anti-horaire).

Quiz Rapide : Testez vos connaissances (Récapitulatif)

1. La flèche d'une poutre est généralement maximale :

2. La rigidité flexionnelle \(EI\) d'une poutre dépend :

3. L'équation différentielle de la déformée d'une poutre est donnée par (pour de petites déformations) :

Glossaire

Déformée (Ligne Élastique)
Forme prise par l'axe longitudinal initialement rectiligne d'une poutre sous l'effet des charges appliquées.
Flèche (\(y(x)\) ou \(v(x)\))
Déplacement transversal d'un point de l'axe neutre de la poutre par rapport à sa position initiale. Unité : mètre (m) ou millimètre (mm).
Rotation (\(\theta(x)\) ou \(y'(x)\))
Angle que fait la tangente à la déformée en un point avec la direction initiale de l'axe de la poutre. Exprimée en radians (rad).
Rigidité Flexionnelle (\(EI\))
Produit du module d'Young (\(E\)) du matériau par le moment d'inertie (\(I\)) de la section transversale de la poutre. Elle caractérise la résistance de la poutre à la flexion. Unité : N.m² ou kN.m².
Méthode de la Double Intégration
Méthode de calcul de la déformée d'une poutre basée sur l'intégration de l'équation différentielle \(EI y'' = M(x)\). La première intégration donne la rotation et la seconde donne la flèche.
Conditions aux Limites
Contraintes géométriques ou cinématiques connues aux appuis de la poutre (par exemple, flèche nulle, rotation nulle) qui permettent de déterminer les constantes d'intégration.
Calcul des Déformations dans une Poutre en RDM - Exercice d'Application

D’autres exercices de Rdm : 

0 commentaires
Soumettre un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *