Module d’Young à partir d’un Essai de Traction
Comprndre le Module d’Young à partir d’un Essai de Traction
Une entreprise de construction doit vérifier les propriétés mécaniques du béton armé utilisé pour la construction d’un pont.
Pour cela, elle procède à un essai de traction sur un échantillon de béton armé afin de déterminer son module d’Young, qui est une mesure de sa rigidité.
Le module d’Young est crucial pour comprendre comment le matériau réagira sous des charges différentes, ce qui est essentiel pour garantir la sécurité et la stabilité du pont.
Pour comprendre la Détermination du Module d’Young et les Contraintes et déformations en traction, cliquez sur les liens.
Données Fournies:
- Longueur initiale de l’échantillon (L₀): 200 cm
- Diamètre de l’échantillon (d): 15 cm
- Charge appliquée (F): Varie de 0 à 500 kN en 5 étapes égales (0, 125 kN, 250 kN, 375 kN, 500 kN).
- Allongements mesurés (ΔL) correspondant à chaque charge: 0 mm, 0.5 mm, 1.0 mm, 1.5 mm, 2.0 mm.
Objectif de l’Exercice:
1. Calculer la contrainte (σ): La contrainte est la force interne générée dans l’échantillon par l’application de la charge externe.
2. Calculer la déformation (ε): La déformation est le changement de longueur par unité de longueur originale.
3. Déterminer le module d’Young (E): Le module d’Young est la pente de la courbe contrainte-déformation dans la région élastique linéaire.
Correction : Module d’Young à partir d’un Essai de Traction
1. Calcul de la contrainte (σ)
La contrainte (σ) est calculée en utilisant la formule
\[ \sigma = \frac{F}{A} \]
où \(F\) est la force appliquée et \(A\) est l’aire de la section transversale de l’échantillon.
L’aire de la section transversale (\(A\)) pour un échantillon cylindrique est donnée par
\[ A = \pi \left(\frac{d}{2}\right)^2 \]
Avec \(d\) étant le diamètre de l’échantillon.
- Diamètre de l’échantillon (\(d\)): 15 cm
- Aire de la section transversale (\(A\)): \(\pi \times (7.5)^2 = 176.71 \text{ cm}^2\)
Pour chaque niveau de charge, la contrainte est calculée comme suit :
- \(F = 0\) kN:
\[ \sigma = \frac{0}{176.71} = 0\, \text{Pa} \]
- \(F = 125\) kN
\[ \sigma = \frac{125,000}{176.71} = 707,107\, \text{Pa} \]
- \(F = 250\) kN
\[ \sigma = \frac{250,000}{176.71} = 1,414,214\, \text{Pa} \]
- \(F = 375\) kN
\[ \sigma = \frac{375,000}{176.71} = 2,121,321\, \text{Pa} \]
- \(F = 500\) kN
\[ \sigma = \frac{500,000}{176.71} = 2,828,427\, \text{Pa} \]
2. Calcul de la déformation (ε)
La déformation (ε) est le rapport de l’allongement (\(\Delta L\)) à la longueur initiale (\(L_0\)) de l’échantillon :
\[ \epsilon = \frac{\Delta L}{L_0} \]
- Longueur initiale (\(L_0\)): 200 cm
Les déformations calculées sont :
- \(\Delta L = 0\) mm
\[ \epsilon = \frac{0}{200} = 0 \]
- \(\Delta L = 0.5\) mm
\[ \epsilon = \frac{0.05}{200} = 0.00025 \]
- \(\Delta L = 1.0\) mm
\[ \epsilon = \frac{0.1}{200} = 0.0005 \]
- \(\Delta L = 1.5\) mm
\[ \epsilon = \frac{0.15}{200} = 0.00075 \]
- \(\Delta L = 2.0\) mm
\[ \epsilon = \frac{0.2}{200} = 0.001 \]
3. Détermination du module d’Young (E)
Le module d’Young (E) est calculé à partir de la pente de la courbe contrainte-déformation dans la région élastique linéaire :
\[ E = \frac{\sigma_2 – \sigma_1}{\epsilon_2 – \epsilon_1} \]
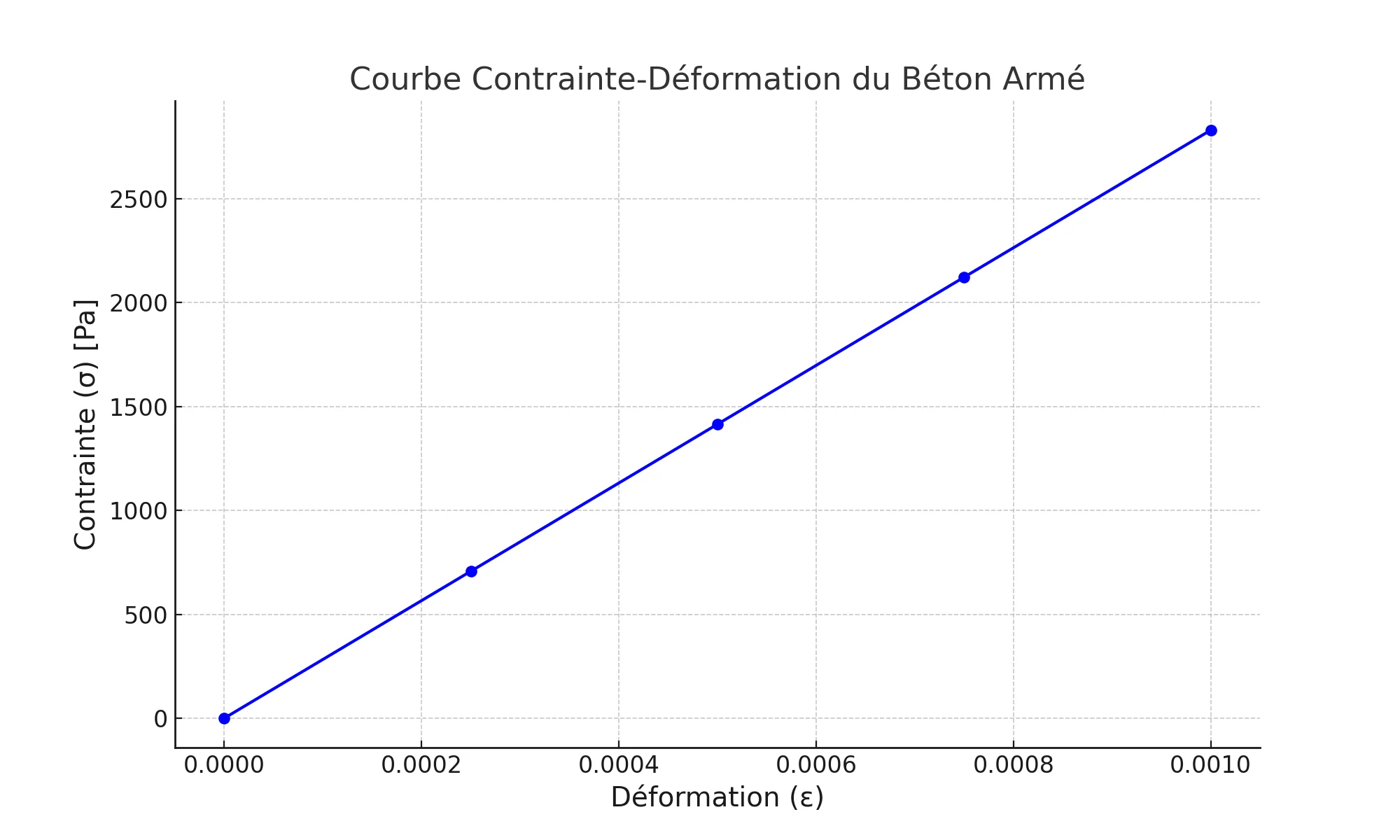
En utilisant les valeurs extrêmes :
- Pour \(\sigma_1 = 0\) Pa et \(\sigma_2 = 2,828,427\) Pa
- Pour \(\epsilon_1 = 0\) et \(\epsilon_2 = 0.001\)
Le module d’Young est donc :
\[ E = \frac{2,828,427 – 0}{0.001 – 0} \] \[ E = 2,828,427 \text{ Pa}, \text{ soit } 2.83 \text{ MPa} \]
Conclusion
Le module d’Young pour cet échantillon de béton armé, déterminé à partir des données de l’essai de traction, est de 2.83 MPa.
Cette valeur reflète la rigidité du matériau, indiquant combien il se déforme sous une charge spécifique.
Ce paramètre est crucial pour la conception et l’analyse structurelle, permettant aux ingénieurs de prévoir le comportement du béton sous des charges variées et de garantir la sécurité et la stabilité des structures en béton armé.
Module d’Young à partir d’un Essai de Traction
D’autres exercices de béton armé:




0 commentaires