Distance entre Deux Collines en Géodésie

Comprendre le Calcul de la Distance entre Deux Collines en Géodésie

Vous travaillez en tant que géodésiste sur un projet de construction d’un pont. Le pont doit enjamber une rivière, reliant deux collines dont les sommets sont visibles et accessibles.

Pour concevoir le pont, vous devez d’abord déterminer la distance exacte entre les deux sommets des collines, en tenant compte de la courbure de la Terre.

Pour comprendre le Calcul de distance en topographie, cliquez sur le lien.

Données

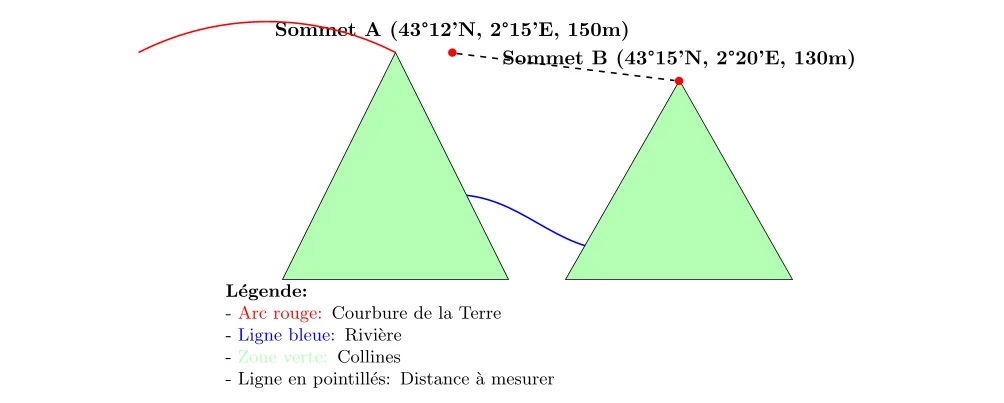
• Les coordonnées géographiques du sommet de la colline A sont 43°12’N, 2°15’E.
• Les coordonnées géographiques du sommet de la colline B sont 43°15’N, 2°20’E.
• La hauteur du sommet A par rapport au niveau de la mer est de 150 mètres.
• La hauteur du sommet B par rapport au niveau de la mer est de 130 mètres.
• Le rayon moyen de la Terre est de 6,371 km.

Questions:

1. Calculez la distance angulaire en degrés entre les deux sommets en utilisant leurs coordonnées géographiques.
2. Convertissez cette distance angulaire en distance linéaire sur la surface terrestre (en considérant la Terre comme une sphère parfaite).
3. Ajustez cette distance en prenant en compte la différence d’altitude entre les deux sommets.

Correction : Distance entre Deux Collines en Géodésie

1. CALCUL DE LA DISTANCE ANGULAIRE

Formule :

La distance angulaire \(D\) entre deux points sur une sphère, donnés par leurs coordonnées de latitude et de longitude, se calcule avec la formule de l’arc cosinus :

\( D = \cos^{-1}\left(\sin(\text{latA}) \cdot \sin(\text{latB}) + \cos(\text{latA}) \cdot \cos(\text{latB}) \cdot \cos(\text{lonA} – \text{lonB})\right) \)

Valeurs substituées :

• Latitude de la colline A (latA) = 43°12’N = 43.2°
• Latitude de la colline B (latB) = 43°15’N = 43.25°
• Longitude de la colline A (lonA) = 2°15’E = 2.25°
• Longitude de la colline B (lonB) = 2°20’E = 2.333°

Convertir les degrés en radians :

\[ \text{latA} = \frac{43.2 \times \pi}{180} \]

\[ \text{latB} = \frac{43.25 \times \pi}{180} \]

\[ \text{lonA} = \frac{2.25 \times \pi}{180} \]

\[ \text{lonB} = \frac{2.333 \times \pi}{180} \]

Substituer et calculer :

\( D = \cos^{-1}\left(\sin(\text{latA_rad}) \cdot \sin(\text{latB_rad}) + \cos(\text{latA_rad}) \cdot \cos(\text{latB_rad}) \cdot \cos(\text{lonA_rad} – \text{lonB_rad})\right) \)

\( D = \cos^{-1}\left(\sin(0.754) \cdot \sin(0.755) + \cos(0.754) \cdot \cos(0.755) \cdot \cos(0.00145)\right) \)

\(= 0.00137286 \text{ radians} \)

2. CONVERSION EN DISTANCE LINÉAIRE

Formule :

La distance linéaire \(L\) sur la surface de la Terre est calculée en multipliant la distance angulaire par le rayon de la Terre :

\[ L = R \cdot D \]

• \(R = 6371 \text{ km} \quad (\text{rayon moyen de la Terre})\)

Calcul :

\[ L = 6371 \times 0.00137286 \] \[ L = 8.746 \text{ km} \]

3. AJUSTEMENT EN FONCTION DE L’ALTITUDE

Formule :

Pour ajuster la distance en prenant en compte les altitudes différentes des sommets, on utilise la formule de la distance dans l’espace :

\[ L_{ajusté} = \sqrt{L^2 + \left(\frac{hA – hB}{1000}\right)^2} \]

• \(hA = 150 \text{ m}\)
• \( hB = 130 \text{ m}\)

Calcul :

Convertir la différence d’altitude de mètres en kilomètres :

\[ L_{ajusté} = \sqrt{8.746^2 + \left(\frac{150 – 130}{1000}\right)^2} \] \[ L_{ajusté} = \sqrt{76.392 + 0.0004} \] \[ L_{ajusté} = 8.74649 \text{ km} \] \[ L_{ajusté} = 8746.49 \text{ m} \]

Distance entre Deux Collines en Géodésie

D’autres exercices de topographie:

• Division d’un Terrain en Topographie
• Méthode de triangulation en topographie
• Levé Planimétrique et Altimétrique