Analyse d’un Réseau Électrique
Comprendre l’Analyse d’un Réseau Électrique
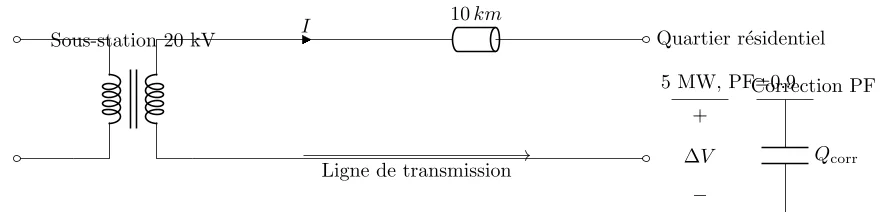
Vous travaillez en tant qu’ingénieur pour une société de distribution d’électricité. On vous a confié la tâche d’analyser une portion du réseau de distribution pour évaluer sa capacité à intégrer un nouveau quartier résidentiel.
Ce quartier est prévu pour consommer en moyenne 5 MW avec un facteur de puissance de 0,9 en retard.
Le réseau de distribution existant est alimenté par une sous-station qui fournit de l’électricité à une tension de 20 kV.
La distance entre la sous-station et le nouveau quartier est de 10 km. Le réseau utilise des câbles triphasés avec une impédance de \(0.5 + j1.5\, \Omega/km\) par phase.
Données:
- Tension d’alimentation de la sous-station: 20 kV
- Consommation moyenne du quartier: 5 MW
- Facteur de puissance initial du quartier: 0,9 (retard)
- Distance sous-station au quartier: 10 km
- Impédance des câbles: \(0.5 + j1.5\, \Omega/km\) par phase
- Limite de chute de tension: 5%
- Facteur de puissance souhaité: 0,95 (retard)
Schéma de distribution électrique:
Questions:
1. Calculer la chute de tension dans les câbles du réseau de distribution et vérifier si elle respecte la norme qui limite la chute de tension à 5% de la tension d’alimentation.
2. Déterminer la puissance réactive supplémentaire nécessaire pour améliorer le facteur de puissance du quartier à 0,95 en retard, afin de réduire les pertes et améliorer l’efficacité du réseau.
Correction : Analyse d’un Réseau Électrique
Partie 1 : Calcul de la Chute de Tension
1. Calcul de l’Impédance Totale du Câble
L’impédance par kilomètre du câble est donnée par \(Z_{\text{par km}} = 0.5 + j1.5\, \Omega/\text{km}\).
Sur une distance de 10 km, l’impédance totale \(Z_{\text{tot}}\) est calculée comme suit:
\[ Z_{\text{tot}} = (0.5 + j1.5) \times 10 \] \[ Z_{\text{tot}} = 5 + j15\, \Omega \]
2. Conversion de la Puissance Consommée en Puissance Apparente
Avec une puissance consommée de 5 MW et un facteur de puissance initial de 0,9 (retard), la puissance apparente \(S\) et la puissance réactive \(Q\) sont calculées comme suit:
- Puissance apparente:
\[ S = \frac{P}{\text{PF}} \] \[ S = \frac{5}{0.9} = 5.56\, \text{MVA} \]
- Puissance réactive:
\[ Q = \sqrt{S^2 – P^2} \] \[ Q = \sqrt{(5.56)^2 – (5)^2} \] \[ Q = 2.48\, \text{MVAR} \]
3. Calcul du Courant dans le Réseau
Le courant \(I\) circulant dans le réseau est déterminé par la formule :
\[ I = \frac{S}{\sqrt{3} \times V_{ll}} \] \[ I = \frac{5.56 \times 10^6}{\sqrt{3} \times 20 \times 10^3} \] \[ I = 160.65\, \text{A} \]
4. Calcul de la Chute de Tension \(\Delta V\)
La chute de tension est obtenue en multipliant le courant par l’impédance totale du câble :
\[ \Delta V = I \times Z_{\text{tot}} \] \[ \Delta V = 160.65 \times (5 + j15) \] \[ \Delta V = 803.25 + j2409.75\, \text{V} \text{ par phase} \]
5. Chute de Tension en Pourcentage
La chute de tension en pourcentage est calculée en convertissant la tension de ligne à tension de phase et en utilisant la magnitude de \(\Delta V\) :
\[ \% \Delta V = \frac{|\Delta V|}{V_{\text{ph}}} \times 100 \]
où
\[ V_{\text{ph}} = \frac{20\, \text{kV}}{\sqrt{3}} = 11.547\, \text{kV} \]
\[ |\Delta V| = \sqrt{(803.25)^2 + (2409.75)^2} \] \[ |\Delta V| = 2500\, \text{V} \],
donc :
\[ \% \Delta V = \frac{2500}{11547} \times 100 \] \[ \% \Delta V \approx 21.6\% \]
Conclusion Partie 1 :
La chute de tension calculée dépasse la limite de 5%, indiquant la nécessité d’une correction.
Partie 2 : Amélioration du Facteur de Puissance
1. Calcul de la Nouvelle Puissance Réactive pour un Facteur de Puissance de 0,95
L’objectif est de réduire la puissance réactive pour atteindre un facteur de puissance de 0,95.
- Nouvelle Puissance Apparente \(S_{\text{new}}\):
La nouvelle puissance apparente est calculée en utilisant le facteur de puissance souhaité de 0,95 :
\[ S_{\text{new}} = \frac{P}{\cos(\phi_{\text{new}})} \] \[ S_{\text{new}} = \frac{5}{0.95} = 5.26\, \text{MVA} \]
- Nouvelle Puissance Réactive \(Q_{\text{new}}\):
La nouvelle puissance réactive est obtenue par la formule suivante :
\[ Q_{\text{new}} = \sqrt{S_{\text{new}}^2 – P^2} \] \[ Q_{\text{new}} = \sqrt{(5.26)^2 – (5)^2} \] \[ Q_{\text{new}} = 1.48\, \text{MVAR} \]
2. Puissance Réactive à Ajouter ou à Retirer:
Pour ajuster la puissance réactive au nouveau besoin, la différence entre la puissance réactive initiale et la nouvelle est calculée comme suit :
\[ \Delta Q = Q_{\text{new}} – Q \] \[ \Delta Q = 1.48 – 2.48 \] \[ \Delta Q = -1\, \text{MVAR} \]
Conclusion Partie 2 :
Pour atteindre un facteur de puissance de 0,95, il est nécessaire de retirer 1 MVAR de puissance réactive. Cela pourrait être réalisé en installant des banques de condensateurs.
Conclusion Générale:
Cette analyse démontre la nécessité de mesures correctives pour intégrer le nouveau quartier au réseau existant tout en maintenant les performances dans les limites acceptables.
La chute de tension doit être minimisée, et l’amélioration du facteur de puissance par l’installation de banques de condensateurs est recommandée pour réduire les pertes d’énergie et améliorer l’efficacité globale du réseau.
Analyse d’un Réseau Électrique
D’autres exercices d’électricité:




0 commentaires