Voile en béton armé Dimensionnement
Comprendre le Voile en béton armé Dimensionnement
Vous êtes un ingénieur structure en charge de la conception d’un immeuble résidentiel de 5 étages situé en bord de mer, une zone exposée à des vents forts. Les voiles en béton armé jouent un rôle clé dans la stabilité latérale du bâtiment et doivent résister à des charges verticales (poids propre, charges permanentes) et horizontales (vent). Une erreur de dimensionnement pourrait entraîner des fissurations, des déformations excessives, voire un effondrement partiel.
Données du projet :
- Environnement : Zone ventée (vitesse du vent élevée), exigences de durabilité accrues en milieu maritime.
- Normes de référence : Eurocode 2 (calcul des structures en béton) et Eurocode 1 (actions sur les structures).
- Enjeux : Optimiser l’épaisseur du voile pour minimiser les coûts tout en garantissant la sécurité.
Problématique :
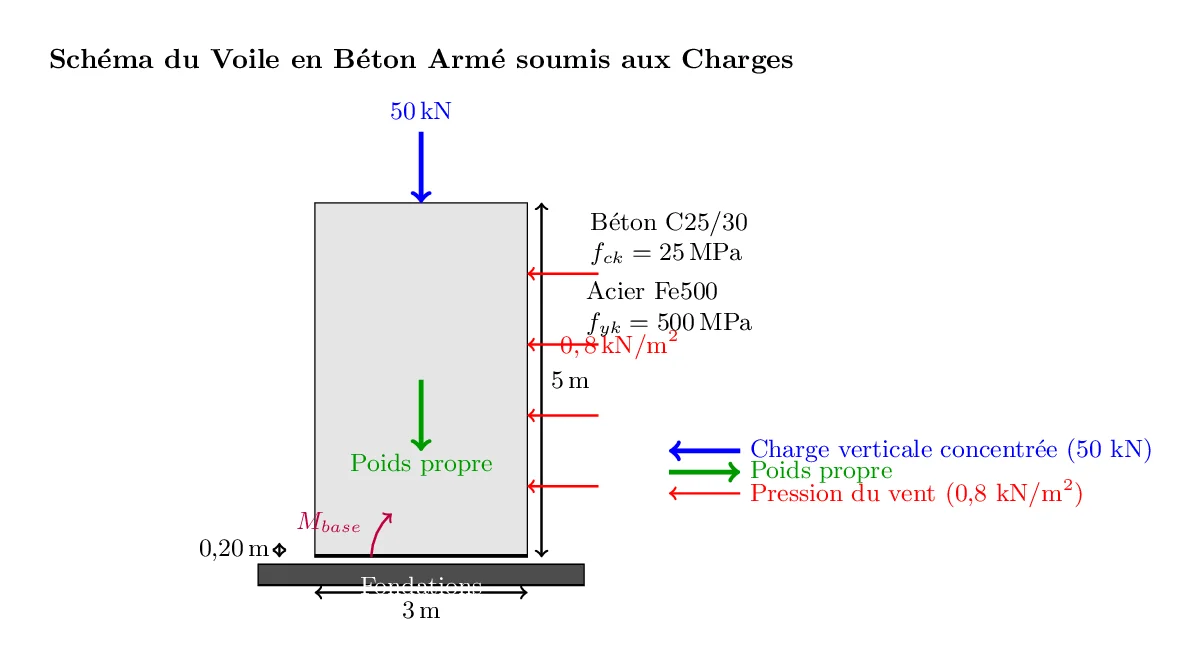
Un voile de 3 m de largeur × 5 m de hauteur (épaisseur initiale proposée : 20 cm) est soumis à :
- Une charge verticale concentrée de 50 kN en tête (issue des planchers supérieurs).
- Une pression horizontale du vent de 0,8 kN/m² (valeur caractéristique).
- Son poids propre (à calculer), combiné à la charge verticale, induit un risque de compression excessive.
- Les efforts de vent génèrent un moment fléchissant et un effort tranchant critiques à la base.
Matériaux utilisés :
- Béton C25/30 : Résistance à la compression \(f_{ck} = 25 \text{ MPa}\) , adapté pour les éléments porteurs.
- Acier Fe500 : Résistance élevée (\( f_{yk} = 500 \, \text{MPa} \)) pour limiter les sections d’armatures.
Questions :
1. Calcul des sollicitations :
- Déterminer le poids propre du voile et la charge horizontale totale due au vent.
- Évaluer le moment fléchissant maximal à la base en combinant charges verticales (excentricité) et vent.
2. Vérification de la résistance :
- Effort tranchant : Vérifier que la contrainte au pied ne dépasse pas la capacité du béton (risque de rupture fragile).
- Flexion : Dimensionner les armatures longitudinales pour reprendre le moment ultime (méthode des sections réduites).
- Compression : S’assurer que la contrainte sous charges verticales reste inférieure à \(0.6f_{ck}\) (marge de sécurité).
3. Optimisation de l’épaisseur :
- Si l’épaisseur initiale de 20 cm est insuffisante, proposer une nouvelle valeur et réitérer les vérifications.
Correction : Dimensionner un voile en béton armé
1. Calcul des sollicitations
1.1. Poids propre du voile
Le poids propre \(G\) du voile dépend de son volume de béton et de la densité (masse volumique) du matériau. En général, on prend pour le béton armé une densité \(\gamma \approx 25\,\text{kN/m}^3\).
Formule:
\[ G = \gamma \times V \]
où
- \(\gamma\) : densité du béton armé (25~kN/m\(^3\)),
- \(V\) : volume du voile.
Données:
- \(L = 3\,\text{m} \quad (\text{largeur}),\)
- \(H = 5\,\text{m} \quad (\text{hauteur}),\)
- \(e = 0{,}20\,\text{m} \quad (\text{épaisseur initiale}),\)
- \(\gamma = 25\,\text{kN/m}^3.\)
Calcul:
\[ V = L \times H \times e \] \[ V = 3 \times 5 \times 0{,}20 = 3\,\text{m}^3, \]
\[ G = \gamma \times V \] \[ G = 25 \times 3 = 75\,\text{kN}. \]
Résultat : Poids propre du voile \(G = 75\,\text{kN}\).
1.2. Charge verticale totale
On nous indique une charge concentrée en tête de 50 kN (provenant des planchers supérieurs).
- \(N_{\text{sup}} = 50\,\text{kN}, \quad G = 75\,\text{kN}\)
a) Charge verticale cumulée.
\[ N_{\text{tot}} = G + N_{\text{sup}} \] \[ N_{\text{tot}} = 75 + 50 \] \[ N_{\text{tot}} = 125\,\text{kN}. \]
Résultat : \(N_{\text{tot}} = 125\,\text{kN}\).
1.3. Charge horizontale due au vent
La pression du vent est donnée \(p = 0{,}8\,\text{kN/m}^2\). La force totale s’obtient en multipliant cette pression par la surface exposée (largeur \(\times\) hauteur).
Formule:
\[ F_{\text{vent}} = p \times S, \]
où
- \(p = 0{,}8\,\text{kN/m}^2\),
- \(S = L \times H\).
Calcul:
\[ S = 3 \times 5 = 15\,\text{m}^2 \]
\[ \Longrightarrow\quad F_{\text{vent}} = 0{,}8 \times 15 \] \[ F_{\text{vent}} = 12\,\text{kN}.\]
Résultat : Effort horizontal total du vent \(F_{\text{vent}} = 12\,\text{kN}\).
1.4. Moment fléchissant maximal à la base
a) Répartition de la pression de vent
Pour une pression de vent uniformément répartie, la résultante s’exerce au milieu de la hauteur, soit à \(H/2 = 2{,}5\,\text{m}\) du bas du voile.
b) Moment dû au vent
\[ M_{\text{vent}} = F_{\text{vent}} \times \frac{H}{2}. \]
c) Prise en compte d’une éventuelle excentricité
Si la charge verticale n’est pas parfaitement centrée, on ajoute un moment d’excentricité :
\[ M_{N} = N_{\text{tot}} \times e,\]
(Hypothèse par exemple \(e = 0{,}05\,\text{m}\) si la charge est légèrement décentrée.)
Calcul numérique:
– Moment dû au vent :
\[ M_{\text{vent}} = 12 \times 2{,}5 = 30\,\text{kN}\cdot\text{m}, \]
– Moment d’excentricité (exemple) :
\[ M_{N} = 125 \times 0{,}05 = 6{,}25\,\text{kN}\cdot\text{m}, \]
– Moment total :
\[ M_{\text{tot}} = M_{\text{vent}} + M_{N} \] \[ M_{\text{tot}} = 30 + 6{,}25 \] \[ M_{\text{tot}} = 36{,}25\,\text{kN}\cdot\text{m}. \]
Résultat : Moment fléchissant maximal à la base \(M_{\text{tot}} \approx 36{,}25\,\text{kN}\cdot\text{m}\).
2. Vérification de la résistance
2.1. Effort tranchant
On compare l’effort tranchant dû au vent à la capacité du voile (résistance au cisaillement du béton + armature). Dans les Eurocodes, on dispose de formules précises (\(V_{Rd,c}, V_{Rd,s}\), etc.) pour la vérification. Ici, on fait un contrôle simplifié de la contrainte de cisaillement.
Formule simplifiée:
\[ \tau_{Ed} = \frac{V_{Ed}}{b \times e}, \]
avec
- \(V_{Ed} = 12\,\text{kN}\),
- \(b = 3\,\text{m}\) (longueur du voile),
- \(e = 0{,}20\,\text{m}\) (épaisseur).
Calcul:
\[ A_{\text{section}} = b \times e \] \[ A_{\text{section}} = 3 \times 0{,}20 = 0{,}60\,\text{m}^2, \]
\[ \tau_{Ed} = \frac{12\,000\,\text{N}}{0{,}60\,\text{m}^2}
\] \[ \tau_{Ed} = 20\,000\,\text{N/m}^2
\] \[ \tau_{Ed} = 0{,}02\,\text{MPa}. \]
Cette valeur est très faible comparée à la résistance au cisaillement typique du béton (souvent > 1 MPa pour du C25/30).
Conclusion tranchant : Le voile est largement suffisant en cisaillement ; aucun risque de rupture fragile au cisaillement.
2.2. Flexion (dimensionnement en armatures longitudinales)
On dimensionne les armatures verticales pour résister au moment ultime \(M_{\text{tot}} = 36{,}25\,\text{kN}\cdot\text{m}\). Le béton en compression est pris en compte dans la partie comprimée, l’acier en traction dans la partie tendue.
Formule (approximation simplifiée):
\[ M_{Ed} \approx A_s \cdot f_{yd} \cdot z, \]
où
- \(A_s : \text{section d’acier requise}\)
- \(f_{yd} = \frac{f_{yk}}{\gamma_s} = \frac{500}{1{,}15} \approx 435\,\text{MPa}\)
- \(z \approx 0{,}9 \, d\)
- \(d \approx e – \text{enrobage}.\)
Données et conversion d’unités:
- \(M_{Ed} = 36{,}25\,\text{kN}\cdot\text{m} = 3{,}625 \times 10^7\,\text{N}\cdot\text{mm}\)
- \(d \approx 0{,}20 – 0{,}03 = 0{,}17\,\text{m} = 170\,\text{mm}\)
- \(z \approx 0{,}9 \times 170 = 153\,\text{mm}\)
- \(f_{yd} \approx 435\,\text{N/mm}^2\)
Calcul de la section d’acier:
\[ A_s = \frac{M_{Ed}}{f_{yd} \times z} \] \[ A_s = \frac{3{,}625 \times 10^7}{435 \times 153} \] \[ A_s \approx 544\,\text{mm}^2. \]
Cette surface d’acier (544 mm²) est la somme nécessaire pour la largeur totale de 3 m.
Remarque : Dans la pratique, la section minimale d’armatures pour un voile (pour des raisons de retrait, de fissuration, etc.) peut être plus élevée que cette valeur « théorique ». Les Eurocodes imposent souvent des ratios minimaux (ex. 0,2% de la section de béton).
2.3. Vérification en compression:
On vérifie que la contrainte de compression dans le béton au pied du voile ne dépasse pas environ \(0{,}6\, f_{ck}\) (marge de sécurité).
Formule:
\[ \sigma_{Ed} = \frac{N_{\text{tot}}}{A_c} \] Avec \[ A_c = b \times e \]
Calcul:
\[ N_{\text{tot}} = 125\,\text{kN} \]
\[ A_c = 3 \times 0{,}20 = 0{,}60\,\text{m}^2 \]
\[ \Longrightarrow\quad \sigma_{Ed} = \frac{125\,000\,\text{N}}{0{,}60\,\text{m}^2} \] \sigma_{Ed} \approx 0{,}208\,\text{MPa}. \]
Comparaison à la limite:
\[ 0{,}6\, f_{ck} = 0{,}6 \times 25 = 15\,\text{MPa}. \]
Or, \(\sigma_{Ed} = 0{,}208\,\text{MPa} \ll 15\,\text{MPa}\).
Conclusion compression : La contrainte de compression est très inférieure à la limite. Le voile ne risque pas l’écrasement.
3. Optimisation de l’épaisseur
3.1. Constat avec 20 cm d’épaisseur
- Les vérifications (cisaillement, flexion, compression) montrent de larges marges de sécurité.
- L’épaisseur de 20 cm semble plus que suffisante pour ce niveau de charges.
3.2. Proposition d’une nouvelle épaisseur
Pour réduire les coûts (béton, armature, etc.), on peut proposer de passer à 15 cm, voire 16-18 cm, en veillant à :
- Respecter les exigences d’enrobage minimal (durabilité en milieu marin),
- Vérifier les contraintes de mise en place des aciers (espacements, recouvrements),
- Ne pas dépasser les limites de flèche ou de stabilité globale.
Exemple : Hypothèse \( e = 15\,\text{cm} \).
- Poids propre :
\[ V = 3 \times 5 \times 0{,}15 = 2{,}25\,\text{m}^3 \]
\[ G = 25 \times 2{,}25 = 56{,}25\,\text{kN} \]
Charge verticale totale :
\[ N_{\text{tot}} = 56{,}25 + 50 = 106{,}25\,\text{kN} \]
- Contrainte de compression :
\[ A_c = 3 \times 0{,}15 = 0{,}45\,\text{m}^2 \]
\[ \Longrightarrow\quad
\sigma_{Ed} \approx \frac{106{,}25}{0{,}45}
\approx 0{,}236\,\text{MPa} \ll 15\,\text{MPa}. \]
Moment fléchissant (toujours environ 36,25 kN·m) : la section d’acier sera légèrement plus élevée car la hauteur utile \(d\) diminue. Cela reste modéré et bien en deçà des limites.
Ainsi, 15 cm d’épaisseur peuvent encore être suffisants, sous réserve de vérifier :
- Les minimums constructifs (armatures, enrobage),
- Les déformations (flèche, stabilité hors-plan),
- Les prescriptions spécifiques au milieu agressif (bord de mer).
Synthèse :
- Les hypothèses de charges et les calculs montrent qu’un voile de 20 cm est très sûr.
- Pour optimiser, on peut réduire l’épaisseur, sans mettre en danger la sécurité, à condition de vérifier la mise en œuvre (armatures, enrobage, etc.) et de tenir compte des aspects de durabilité en milieu maritime.
Voile en béton armé Dimensionnement
D’autres exercices de béton armé :















0 commentaires