EGC

Vérification du Non-Poinçonnement du Sol

Vérification du Non-Poinçonnement du Sol en Géotechnique

Vérification du Non-Poinçonnement du Sol

Contexte : La fondation, premier maillon de la sécurité d'un ouvrage.

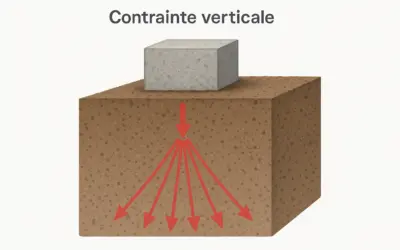
En géotechnique, la vérification au poinçonnement est une étape cruciale du dimensionnement des fondations superficielles (appelées "semelles"). Elle garantit que la charge concentrée apportée par un poteau ne va pas "percer" le sol comme un couteau dans du beurre. Cet état limite ultime (ELU) peut entraîner un tassement brutal et la ruine de l'ouvrage. Cet exercice, basé sur les principes de l'Eurocode 7Norme européenne pour le calcul géotechnique (NF EN 1997). Elle définit les méthodes de calcul et les coefficients de sécurité à appliquer pour garantir la stabilité des ouvrages en interaction avec le sol., vous guidera dans la vérification de la sécurité d'une semelle vis-à-vis de ce risque.

Remarque Pédagogique : Cet exercice illustre parfaitement l'interface entre le génie civil (calcul des charges de la structure) et la géotechnique (analyse de la réponse du sol). Nous allons utiliser des charges issues d'un bâtiment pour vérifier si le sol sous-jacent est capable de les supporter sans rupture par poinçonnement. C'est un calcul fondamental pour tout ingénieur structure ou géotechnicien.

Objectifs Pédagogiques

  • Calculer une charge de calcul à l'État Limite Ultime (ELU) selon l'Eurocode.
  • Déterminer la contrainte appliquée par une fondation sur le sol.
  • Calculer la capacité portanteC'est la contrainte maximale que le sol peut supporter avant de rompre. Elle dépend des caractéristiques du sol (cohésion, angle de frottement) et de la géométrie de la fondation. du sol sous une semelle.
  • Vérifier la sécurité au poinçonnement en comparant la contrainte et la résistance.
  • Comprendre l'influence des caractéristiques du sol (cohésion, angle de frottement) sur la sécurité.

Données de l'étude

On étudie une semelle de fondation carrée, isolée, en béton armé. Elle supporte un poteau centré qui transmet des charges permanentes et d'exploitation. Le sol de fondation est un sable argileux. Les données du projet sont les suivantes :

Schéma de la fondation et du sol
Sol : Sable argileux γ = 18 kN/m³ c' = 15 kPa φ' = 25° G, Q B = 2.0 m b = 0.4 m
Paramètre Symbole Valeur Unité
Largeur de la semelle \(B\) 2.0 \(\text{m}\)
Largeur du poteau \(b\) 0.4 \(\text{m}\)
Charge permanente \(G_k\) 800 \(\text{kN}\)
Charge d'exploitation \(Q_k\) 450 \(\text{kN}\)
Poids volumique du sol \(\gamma\) 18 \(\text{kN/m³}\)
Cohésion effective du sol \(c'\) 15 \(\text{kPa}\)
Angle de frottement effectif \(\phi'\) 25 \(\text{degrés}\)

Questions à traiter

  1. Calculer l'effort normal de calcul à l'ELU, \(N_{\text{Ed}}\), transmis par le poteau.
  2. Calculer la contrainte de calcul appliquée par la semelle sur le sol, \(\sigma_{\text{Ed}}\).
  3. Calculer la résistance de calcul du sol au poinçonnement (capacité portante), \(q_{\text{R,d}}\).
  4. Vérifier la sécurité de la fondation vis-à-vis du poinçonnement.

Les bases de la Géotechnique (Eurocode 7)

Avant la correction, rappelons quelques concepts fondamentaux pour les fondations superficielles.

1. Combinaison d'actions à l'ELU :
Pour vérifier la résistance, on utilise les charges majorées. La combinaison fondamentale selon l'Eurocode est (pour le bâtiment) : \[ N_{\text{Ed}} = 1.35 \cdot G_k + 1.50 \cdot Q_k \] Où \(G_k\) est la charge permanente et \(Q_k\) la charge d'exploitation. \(N_{\text{Ed}}\) est la charge de calcul que la fondation et le sol doivent pouvoir supporter.

2. Contrainte sur le sol :
La charge \(N_{\text{Ed}}\) est transmise au sol via la surface de la semelle \(A = B^2\). La contrainte moyenne appliquée est simplement : \[ \sigma_{\text{Ed}} = \frac{N_{\text{Ed}}}{A} \] On néglige ici le poids propre de la semelle pour simplifier, bien qu'en pratique il faille l'ajouter à \(N_{\text{Ed}}\).

3. Capacité Portante (Formule de Terzaghi/Brinch Hansen) :
La résistance du sol est complexe. Pour une semelle carrée en conditions drainées, l'Eurocode 7 propose une formule de la forme : \[ q_{\text{R,k}} = c'N_c s_c + q'N_q s_q + 0.5 \gamma' B' N_\gamma s_\gamma \] Où les \(N_c, N_q, N_\gamma\) sont des facteurs de portance (dépendant de \(\phi'\)) et les \(s_c, s_q, s_\gamma\) sont des facteurs de forme. La résistance de calcul \(q_{\text{R,d}}\) est obtenue en divisant la résistance caractéristique \(q_{\text{R,k}}\) par un coefficient de sécurité \(\gamma_R\).

Correction : Vérification du Non-Poinçonnement du Sol

Question 1 : Calculer l'effort normal de calcul (\(N_{\text{Ed}}\))

Principe (le concept physique)

La première étape de toute vérification à l'État Limite Ultime (ELU) est de déterminer la sollicitation la plus défavorable que la structure subira au cours de sa vie. Pour cela, on majore les charges caractéristiques (valeurs "probables") par des coefficients de sécurité partiels (\(\gamma_G\) et \(\gamma_Q\)). Cela permet de prendre en compte les incertitudes sur les charges réelles (ex: plus de neige que prévu, mobilier plus lourd).

Mini-Cours (approfondissement théorique)

La méthode des coefficients partiels (ou méthode des états limites) est une approche semi-probabiliste. Elle garantit un niveau de sécurité cible en majorant les actions (charges) et en minorant les résistances des matériaux (acier, béton, sol) par des coefficients définis dans les normes. L'objectif est de s'assurer que, même dans une situation défavorable, la résistance reste supérieure à la sollicitation.

Remarque Pédagogique (le conseil du professeur)

Imaginez que vous construisez un pont en corde. Vous ne prendriez pas simplement le poids moyen des personnes. Vous considéreriez une situation "pire cas" : un groupe de personnes plus lourdes que la moyenne, toutes serrées au milieu. Les coefficients 1.35 et 1.50 jouent ce rôle : ils transforment les charges "de tous les jours" en charges "de calcul" pour concevoir une structure robuste.

Normes (la référence réglementaire)

La combinaison d'actions \(1.35G_k + 1.50Q_k\) est la combinaison fondamentale de l'Eurocode 0 (EN 1990) pour les états limites ultimes en bâtiment. Elle est utilisée pour vérifier la résistance des éléments structuraux (poutres, poteaux) et des fondations.

Formule(s) (l'outil mathématique)

La formule à appliquer est la combinaison d'actions à l'ELU :

\[ N_{\text{Ed}} = \gamma_G \cdot G_k + \gamma_Q \cdot Q_k \]

Avec \(\gamma_G = 1.35\) et \(\gamma_Q = 1.50\).

Hypothèses (le cadre du calcul)

On suppose que les charges Gk et Qk sont des actions indépendantes et que la combinaison fondamentale de l'EN 1990 est applicable, sans tenir compte d'autres actions comme le vent ou la neige pour cet exemple simplifié.

Donnée(s) (les chiffres d'entrée)
  • Charge permanente, \(G_k = 800 \, \text{kN}\)
  • Charge d'exploitation, \(Q_k = 450 \, \text{kN}\)
Astuces(Pour aller plus vite)

Pour un calcul rapide, on peut estimer que la charge de calcul est environ 1.4 fois la somme des charges caractéristiques. Ici, \(1.4 \times (800+450) = 1750\) kN, ce qui est très proche du résultat exact. C'est un bon moyen de vérifier un ordre de grandeur.

Schéma (Avant les calculs)
Combinaison des charges caractéristiques
Gk = 800Qk = 450+→N_Ed = ?
Calcul(s) (l'application numérique)

On applique la combinaison de charges :

\[ \begin{aligned} N_{\text{Ed}} &= (1.35 \cdot 800 \, \text{kN}) + (1.50 \cdot 450 \, \text{kN}) \\ &= 1080 \, \text{kN} + 675 \, \text{kN} \\ &= 1755 \, \text{kN} \end{aligned} \]
Schéma (Après les calculs)
Résultat de la charge de calcul ELU
1.35*Gk = 10801.5*Qk = 675N_Ed = 1755 kN
Réflexions (l'interprétation du résultat)

L'effort de calcul \(N_{\text{Ed}}\) est de 1755 kN. C'est cette valeur, bien supérieure à la somme des charges caractéristiques (1250 kN), que le système de fondation doit être capable de supporter en toute sécurité. Cette majoration est la première étape de la conception sécuritaire.

Points de vigilance (les erreurs à éviter)

Attention à ne pas inverser les coefficients 1.35 et 1.50. La charge d'exploitation, plus variable et incertaine, reçoit toujours le coefficient le plus élevé. Il faut aussi s'assurer d'utiliser la bonne combinaison d'actions (par exemple, les combinaisons sismiques ou accidentelles ont des coefficients différents).

Points à retenir (permettre a l'apprenant de maitriser la question)
  • Les calculs de résistance se font à l'ELU (État Limite Ultime).
  • On majore les charges caractéristiques (\(G_k, Q_k\)) avec des coefficients partiels.
  • La combinaison usuelle est \(1.35 G_k + 1.50 Q_k\).
Le saviez-vous ? (la culture de l'ingénieur)

La méthode des états limites a été développée dans les années 1960-70, notamment en Europe du Nord et de l'Est, pour remplacer l'ancienne méthode des "contraintes admissibles". Elle offre une approche plus rationnelle et plus homogène de la sécurité des structures.

FAQ (pour lever les doutes)
Pourquoi les coefficients sont-ils 1.35 et 1.50 ?

Ces valeurs sont issues d'analyses statistiques et de calibrations complexes. Elles sont choisies pour garantir une probabilité de défaillance très faible (typiquement de l'ordre de 10⁻⁶ par an) sur la durée de vie de l'ouvrage, en tenant compte des variabilités statistiques des charges et des résistances.

Résultat Final (la conclusion chiffrée)
L'effort normal de calcul à l'ELU est de 1755 kN.
A vous de jouer(pour verifier la comprehension de l'etudiant parrapport a la question)

Si la charge permanente était de 1000 kN et la charge d'exploitation de 300 kN, quel serait le nouvel effort \(N_{\text{Ed}}\) en kN ?

Question 2 : Calculer la contrainte de calcul sur le sol (\(\sigma_{\text{Ed}}\))

Principe (le concept physique)

La force concentrée venant du poteau est "étalée" par la semelle de fondation sur une plus grande surface pour réduire la pression sur le sol. La contrainte est simplement cette force répartie sur l'aire de la base de la semelle. L'objectif est de s'assurer que cette pression reste inférieure à ce que le sol peut encaisser.

Mini-Cours (approfondissement théorique)

La distribution de la contrainte sous une semelle dépend de sa rigidité. Une semelle parfaitement rigide sur un sol élastique crée une distribution de contrainte non uniforme (plus élevée sur les bords pour un sol argileux, au centre pour un sol sableux). Cependant, pour le calcul à l'ELU, on suppose une rupture du sol, et l'hypothèse d'une contrainte uniforme est jugée suffisamment précise et simple à utiliser.

Remarque Pédagogique (le conseil du professeur)

C'est le principe de la raquette à neige. Votre poids (la force) est constant, mais en augmentant la surface de contact avec la neige (le sol), vous diminuez la pression (la contrainte) et évitez de vous enfoncer. Une fondation joue exactement le même rôle pour un bâtiment.

Normes (la référence réglementaire)

L'Eurocode 7 spécifie que l'aire de la fondation à utiliser pour le calcul de la contrainte est l'aire effective \(A'\). Dans le cas d'une charge centrée comme ici, l'aire effective est simplement l'aire géométrique de la base de la semelle.

Formule(s) (l'outil mathématique)

La contrainte est la force divisée par la surface :

\[ \sigma_{\text{Ed}} = \frac{N_{\text{Ed}}}{A} \quad \text{avec} \quad A = B \times B = B^2 \]
Hypothèses (le cadre du calcul)

On suppose que la charge est parfaitement centrée et que la semelle est rigide, ce qui conduit à une distribution de contrainte uniforme sous la semelle. On néglige le poids de la semelle et des terres au-dessus, ce qui est une simplification (approche non conservative, mais acceptable pour cet exercice pédagogique).

Donnée(s) (les chiffres d'entrée)
  • Effort de calcul, \(N_{\text{Ed}} = 1755 \, \text{kN}\) (de Q1)
  • Largeur de la semelle, \(B = 2.0 \, \text{m}\)
Astuces(Pour aller plus vite)

Pour une semelle carrée, la contrainte est \(N_{\text{Ed}}/B^2\). Un calcul mental rapide : \(1755 / (2 \times 2) = 1755 / 4\), ce qui est un peu moins de \(1800/4 = 450\). Cela donne un excellent ordre de grandeur du résultat attendu.

Schéma (Avant les calculs)
Répartition de la charge sur la surface
N_Edσ_Ed = ?Surface A = B²
Calcul(s) (l'application numérique)

1. Calculer la surface de la semelle :

\[ \begin{aligned} A &= (2.0 \, \text{m})^2 \\ &= 4.0 \, \text{m}^2 \end{aligned} \]

2. Calculer la contrainte :

\[ \begin{aligned} \sigma_{\text{Ed}} &= \frac{1755 \, \text{kN}}{4.0 \, \text{m}^2} \\ &= 438.75 \, \text{kPa} \end{aligned} \]
Schéma (Après les calculs)
Contrainte de calcul sous la semelle
σ_Ed = 438.75 kPa
Réflexions (l'interprétation du résultat)

La fondation applique une pression de calcul de près de 439 kPa (soit environ 4.4 bar, ou le poids de 44 tonnes sur 1 m²) sur le sol. C'est cette valeur que nous allons maintenant comparer à la résistance du sol.

Points de vigilance (les erreurs à éviter)

L'erreur la plus commune est une erreur d'unité. Assurez-vous de travailler en unités cohérentes (kN et m). Un oubli de mettre au carré la largeur B est aussi fréquent. En pratique, ne pas oublier d'ajouter le poids de la semelle et des terres à \(N_{\text{Ed}}\) avant de diviser par A.

Points à retenir (permettre a l'apprenant de maitriser la question)
  • La contrainte est la force (de calcul) divisée par la surface.
  • Pour une semelle carrée, la surface est \(A=B^2\).
  • L'unité de contrainte en géotechnique est le kPa (kiloPascal), qui équivaut à un kN/m².
Le saviez-vous ? (la culture de l'ingénieur)

Pour mesurer la pression de contact réelle sous les fondations, les chercheurs utilisent des capteurs de pression (cellules de charge plates) installés à l'interface entre le béton et le sol. Ces mesures expérimentales permettent de valider et d'affiner les modèles de calcul théoriques.

FAQ (pour lever les doutes)
Et si la charge n'est pas centrée ?

Si la charge est excentrée, la distribution de contrainte n'est plus uniforme. Elle devient trapézoïdale ou triangulaire. La contrainte maximale se situe sur le bord le plus chargé et est bien plus élevée que la contrainte moyenne. Le calcul est plus complexe et doit prendre en compte le moment de flexion transmis à la fondation.

Résultat Final (la conclusion chiffrée)
La contrainte de calcul appliquée sur le sol est de 438.75 kPa.
A vous de jouer(pour verifier la comprehension de l'etudiant parrapport a la question)

Si la semelle avait une largeur B de 2.5 m, quelle serait la nouvelle contrainte en kPa ?

Question 3 : Calculer la résistance de calcul du sol (\(q_{\text{R,d}}\))

Principe (le concept physique)

La capacité portante du sol est sa résistance intrinsèque à une charge verticale. Elle dépend de trois composantes : sa cohésion (c' - l'effet "colle" entre les grains), son frottement interne (\(\phi'\) - l'engrènement des grains les uns avec les autres) et le poids des terres avoisinantes (le terme de surface q'). Pour cet exercice, nous utiliserons les formules et coefficients de l'Eurocode 7.

Mini-Cours (approfondissement théorique)

La formule de capacité portante est la superposition de trois solutions théoriques : la portance d'un sol purement cohérent (\(c'\)), la portance d'un sol purement frottant sans poids (\(q'\)), et la portance d'un sol purement frottant avec un poids (\(\gamma\)). Les facteurs de portance \(N\) traduisent la forme des surfaces de rupture dans le sol, tandis que les facteurs de forme \(s\) adaptent la solution (valable pour une semelle infiniment longue) à une géométrie réelle (carrée, circulaire, etc.).

Remarque Pédagogique (le conseil du professeur)

Imaginez que vous marchez sur la plage. Sur le sable sec et lâche (faible \(\phi'\), c'=0), vous vous enfoncez. Sur le sable humide et compact (bon \(\phi'\), un peu de cohésion apparente), vous tenez bien. Sur de l'argile ferme (c' élevé), vous êtes très stable. La formule de portance quantifie simplement ces observations : un sol avec une cohésion et un angle de frottement élevés sera bien plus résistant.

Normes (la référence réglementaire)

L'Eurocode 7 (Annexe D) fournit des formules pour calculer la capacité portante. Pour un sol avec friction et cohésion (conditions drainées), on utilise la formule de Brinch Hansen. Les facteurs de portance \(N_q, N_c, N_\gamma\) sont des fonctions de l'angle de frottement \(\phi'\).

Formule(s) (l'outil mathématique)

1. Facteurs de portance pour \(\phi' = 25^\circ\) :

\[ N_q = e^{\pi \tan\phi'} \tan^2(45^\circ + \phi'/2) \approx 10.66 \]
\[ N_c = (N_q - 1) \cot\phi' \approx 20.72 \]
\[ N_\gamma = 2(N_q - 1) \tan\phi' \approx 9.01 \]

2. Facteurs de forme pour une semelle carrée :

\[ s_q = 1 + \sin\phi' \approx 1.42 \]\[ s_\gamma = 0.7 \]\[ s_c = \frac{s_q N_q - 1}{N_q - 1} \approx 1.46 \]

3. Capacité portante caractéristique (en négligeant le terme de profondeur q') :

\[ q_{\text{R,k}} = c'N_c s_c + 0.5 \gamma B N_\gamma s_\gamma \]

4. Résistance de calcul (avec \(\gamma_{\text{R,v}} = 1.4\) pour la résistance du sol) :

\[ q_{\text{R,d}} = \frac{q_{\text{R,k}}}{\gamma_{\text{R,v}}} \]
Hypothèses (le cadre du calcul)

On fait les hypothèses suivantes : le sol est homogène, la surface du sol est horizontale, la charge est verticale et centrée, et le calcul est mené en conditions drainées (à long terme).

Donnée(s) (les chiffres d'entrée)
  • \(c' = 15 \, \text{kPa}\)
  • \(\phi' = 25^\circ\)
  • \(\gamma = 18 \, \text{kN/m³}\)
  • \(B = 2.0 \, \text{m}\)
Astuces(Pour aller plus vite)

Les facteurs de portance sont souvent disponibles dans des abaques ou des tableurs. Il n'est pas toujours nécessaire de les recalculer à la main. Pour un sol avec une cohésion non nulle, le premier terme (\(c'N_c s_c\)) est souvent prépondérant, surtout pour les semelles de petite taille.

Schéma (Avant les calculs)
Composantes de la Capacité Portante
Cône de ruptureCohésion c'Frottement φ'Poids γ
Calcul(s) (l'application numérique)

1. Calculer les deux termes de la portance :

\[ \begin{aligned} \text{Terme de cohésion} &= c'N_c s_c \\ &= 15 \cdot 20.72 \cdot 1.46 \\ &\approx 453.8 \, \text{kPa} \end{aligned} \]
\[ \begin{aligned} \text{Terme de poids} &= 0.5 \gamma B N_\gamma s_\gamma \\ &= 0.5 \cdot 18 \cdot 2.0 \cdot 9.01 \cdot 0.7 \\ &\approx 113.5 \, \text{kPa} \end{aligned} \]

2. Sommer pour obtenir la résistance caractéristique :

\[ \begin{aligned} q_{\text{R,k}} &= 453.8 + 113.5 \\ &= 567.3 \, \text{kPa} \end{aligned} \]

3. Appliquer le coefficient de sécurité pour obtenir la résistance de calcul :

\[ \begin{aligned} q_{\text{R,d}} &= \frac{q_{\text{R,k}}}{\gamma_{\text{R,v}}} \\ &= \frac{567.3 \, \text{kPa}}{1.4} \\ &\approx 405.2 \, \text{kPa} \end{aligned} \]
Schéma (Après les calculs)
Contribution à la Résistance Caractéristique
Terme Poids (114)Terme Cohésion (454)kPa
Réflexions (l'interprétation du résultat)

Le sol, en tenant compte des incertitudes (via le coefficient \(\gamma_{\text{R,v}}=1.4\)), est capable de résister à une pression de 405.2 kPa. On voit que la cohésion est le paramètre qui contribue le plus (environ 80%) à la résistance dans ce cas précis.

Points de vigilance (les erreurs à éviter)

Les formules de capacité portante sont complexes. Une erreur dans le calcul des facteurs N ou des facteurs de forme s est fréquente. Il faut aussi bien identifier si le calcul doit se faire en conditions "drainées" (avec c' et \(\phi'\), pour les chargements lents sur sols grenus/argileux) ou "non drainées" (avec la cohésion non drainée \(c_u\), pour les chargements rapides sur argiles saturées).

Points à retenir (permettre a l'apprenant de maitriser la question)
  • La résistance du sol dépend de sa cohésion (\(c'\)) et de son angle de frottement (\(\phi'\)).
  • La formule de portance additionne plusieurs termes (cohésion, surcharge, poids du sol).
  • La résistance de calcul \(q_{\text{R,d}}\) est obtenue en divisant la résistance caractéristique \(q_{\text{R,k}}\) par un coefficient de sécurité (\(\gamma_{\text{R,v}} = 1.4\)).
Le saviez-vous ? (la culture de l'ingénieur)

Pour déterminer la capacité portante in-situ, les ingénieurs réalisent des essais de chargement à la plaque. On applique une charge croissante sur une plaque d'acier rigide posée sur le sol et on mesure son enfoncement. La courbe charge-tassement obtenue permet d'estimer expérimentalement la portance du sol à cet endroit.

FAQ (pour lever les doutes)
Pourquoi néglige-t-on le terme de surcharge q' ?

Le terme de surcharge q' représente le poids des terres à côté de la fondation. Si la fondation est posée en surface, ce terme est nul. S'il y a un niveau d'excavation, on devrait le prendre en compte (\(q' = \gamma \cdot D\), où D est la profondeur d'encastrement). Nous l'avons négligé ici pour simplifier, ce qui est une hypothèse conservative (elle réduit la résistance calculée).

Résultat Final (la conclusion chiffrée)
La résistance de calcul du sol au poinçonnement est d'environ 405.2 kPa.
A vous de jouer(pour verifier la comprehension de l'etudiant parrapport a la question)

Si l'angle de frottement \(\phi'\) était de 30° (\(N_c\approx30.1\), \(N_\gamma\approx22.4\), \(s_c\approx1.57\), \(s_q\approx1.5\)), quelle serait la nouvelle résistance de calcul \(q_{\text{R,d}}\) en kPa ?

Question 4 : Vérifier la sécurité vis-à-vis du poinçonnement

Principe (le concept physique)

C'est l'étape finale et la plus simple : on compare la sollicitation (ce que l'on applique) à la résistance (ce que le sol peut supporter). Pour que la fondation soit sécuritaire, la sollicitation de calcul doit être inférieure ou égale à la résistance de calcul. On peut aussi exprimer cette sécurité par un ratio (ou taux de travail), qui doit être inférieur à 100%.

Mini-Cours (approfondissement théorique)

L'inéquation fondamentale du calcul aux états limites est \(E_d \le R_d\), où \(E_d\) est la valeur de calcul de l'effet des actions (sollicitation) et \(R_d\) est la valeur de calcul de la résistance. Dans notre cas, \(E_d = \sigma_{\text{Ed}}\) et \(R_d = q_{\text{R,d}}\). Cette approche garantit que la marge de sécurité entre ce que la structure subit et ce qu'elle peut supporter est suffisante.

Remarque Pédagogique (le conseil du professeur)

Pensez à une balance. D'un côté, vous mettez la charge de calcul (\(\sigma_{\text{Ed}}\)). De l'autre, la résistance de calcul (\(q_{\text{R,d}}\)). Pour que la structure soit stable, le plateau de la résistance doit toujours être plus bas (ou au même niveau) que celui de la charge. Si le plateau de la charge descend plus bas, la balance bascule : c'est la rupture.

Normes (la référence réglementaire)

La vérification \(E_d \le R_d\) est le principe de base de toutes les vérifications à l'ELU, tel que défini dans l'Eurocode 0 (EN 1990, section 6). C'est le cœur de la philosophie de conception des Eurocodes.

Formule(s) (l'outil mathématique)

La condition de non-poinçonnement est :

\[ \sigma_{\text{Ed}} \le q_{\text{R,d}} \]
Hypothèses (le cadre du calcul)

On suppose que les valeurs de \(\sigma_{\text{Ed}}\) et \(q_{\text{R,d}}\) calculées précédemment sont correctes et représentatives du problème. On suppose également que le poinçonnement est le mode de rupture prédominant, et que d'autres vérifications (tassement, glissement) seront faites par ailleurs.

Donnée(s) (les chiffres d'entrée)
  • Contrainte de calcul, \(\sigma_{\text{Ed}} = 438.75 \, \text{kPa}\) (de Q2)
  • Résistance de calcul, \(q_{\text{R,d}} = 405.2 \, \text{kPa}\) (de Q3)
Astuces(Pour aller plus vite)

Le "taux de travail", calculé comme \(\sigma_{\text{Ed}} / q_{\text{R,d}}\), est un indicateur très pratique. Les ingénieurs visent souvent un taux de travail entre 80% et 95%. En dessous, la fondation est peut-être surdimensionnée et coûteuse. Au-dessus de 100%, elle est non conforme.

Schéma (Avant les calculs)
Comparaison de la Contrainte et de la Résistance
Contrainte σ_Ed = 438.75 kPaRésistance q_Rd = 405.2 kPa?
Calcul(s) (l'application numérique)

On compare les deux valeurs :

\[ 438.75 \, \text{kPa} \le 405.2 \, \text{kPa} \quad \Rightarrow \quad \text{FAUX} \]

On peut calculer le ratio de vérification :

\[ \begin{aligned} \text{Ratio} &= \frac{\sigma_{\text{Ed}}}{q_{\text{R,d}}} \\ &= \frac{438.75}{405.2} \\ &\approx 1.08 \end{aligned} \]
Schéma (Après les calculs)
Vérification de la Sécurité
Résistance q_Rd = 405.2 kPaContrainte σ_Ed = 438.75 kPaNON VALIDE ❌
Réflexions (l'interprétation du résultat)

La contrainte appliquée (439 kPa) est supérieure à la résistance du sol (405 kPa). Le ratio de 1.08 (soit 108%) confirme que la fondation n'est PAS SÉCURITAIRE vis-à-vis du poinçonnement. L'ingénieur doit donc redimensionner la fondation. La solution la plus simple est d'augmenter la largeur B de la semelle pour réduire la contrainte appliquée \(\sigma_{\text{Ed}}\) jusqu'à ce qu'elle devienne inférieure à \(q_{\text{R,d}}\).

Points de vigilance (les erreurs à éviter)

Ne jamais conclure sur la base des valeurs caractéristiques. La vérification de sécurité doit impérativement se faire en comparant les valeurs de calcul (design values), c'est-à-dire après application de tous les coefficients de sécurité partiels sur les actions et sur les résistances.

Points à retenir (permettre a l'apprenant de maitriser la question)
  • La sécurité est vérifiée si : Action de Calcul \(\le\) Résistance de Calcul.
  • Pour le poinçonnement : \(\sigma_{\text{Ed}} \le q_{\text{R,d}}\).
  • Si la condition n'est pas respectée, la fondation doit être redimensionnée (généralement en augmentant sa surface).
Le saviez-vous ? (la culture de l'ingénieur)

Les logiciels modernes de calcul de fondations peuvent tester des milliers de dimensions de semelles en quelques secondes pour trouver la solution la plus économique qui respecte toutes les conditions réglementaires (poinçonnement, glissement, tassement, etc.), un processus qui prenait des heures de calcul manuel auparavant.

FAQ (pour lever les doutes)
Quelles sont les autres vérifications à faire sur une fondation ?

Outre le poinçonnement (résistance du sol), il faut vérifier la résistance du béton de la semelle elle-même (flexion et cisaillement). Il faut aussi vérifier les États Limites de Service (ELS), principalement le tassement, pour s'assurer que le bâtiment ne s'enfoncera pas de manière excessive ou différentielle, ce qui pourrait causer des fissures dans la structure.

Résultat Final (la conclusion chiffrée)
La fondation ne vérifie pas la condition de non-poinçonnement (438.75 kPa > 405.2 kPa). Le projet doit être modifié.
A vous de jouer(pour verifier la comprehension de l'etudiant parrapport a la question)

Quelle largeur minimale B (en m, à 0.1 m près) faudrait-il pour que la fondation soit juste sécuritaire (\(\sigma_{\text{Ed}} \approx q_{\text{R,d}}\)) ? (Attention, la résistance \(q_{\text{R,d}}\) dépend aussi un peu de B).

Outil Interactif : Paramètres de Fondation

Modifiez les paramètres du sol et de la fondation pour voir leur influence sur la sécurité au poinçonnement.

Paramètres d'Entrée
2.0 m
15 kPa
25 °
Résultats Clés
Contrainte Appliquée \(\sigma_{\text{Ed}}\) (kPa) -
Résistance du Sol \(q_{\text{R,d}}\) (kPa) -
Ratio de Sécurité (\(\sigma_{\text{Ed}}/q_{\text{R,d}}\)) -

Le Saviez-Vous ?

Karl von Terzaghi (1883-1963) est considéré comme le "père de la mécanique des sols moderne". Ingénieur autrichien puis américain, il a formalisé le concept de contrainte effective, qui est la pierre angulaire de toute la géotechnique. Ses travaux ont transformé une discipline empirique en une véritable science de l'ingénieur, permettant la construction d'ouvrages toujours plus audacieux sur des sols difficiles.

Foire Aux Questions (FAQ)

Que se passe-t-il si une fondation poinçonne le sol ?

Le poinçonnement est une rupture fragile. Le sol sous la fondation cède brusquement, formant un cône de rupture qui remonte vers la surface. Cela se traduit par un enfoncement important et rapide de la fondation, pouvant causer l'effondrement du poteau qu'elle supporte et potentiellement de toute une partie de la structure. C'est un mode de ruine à éviter à tout prix.

La présence d'une nappe phréatique change-t-elle les calculs ?

Oui, de manière significative. La présence d'eau dans le sol réduit les contraintes effectives (le poids des terres est "allégé" par la poussée d'Archimède). On doit alors utiliser le poids volumique déjaugé (\(\gamma'\)) dans les calculs, ce qui diminue la capacité portante (le terme en \(N_\gamma\)) et rend le sol moins résistant. C'est un point de vigilance majeur dans tout projet géotechnique.

Quiz Final : Testez vos connaissances

1. Si la cohésion c' du sol est nulle (sable pur), la capacité portante...

2. Pour améliorer la sécurité au poinçonnement d'une semelle existante qui est jugée insuffisante, la solution la plus courante est de...

Poinçonnement
Mode de rupture du sol sous une charge concentrée, où un cône de sol s'enfonce sous la fondation. C'est un état limite ultime de capacité portante.
Capacité Portante
Contrainte maximale que le sol peut supporter avant de rompre. Elle est calculée en fonction des propriétés du sol (c', φ', γ) et de la géométrie de la fondation.
Eurocode 7
Norme européenne de calcul géotechnique qui définit les approches de calcul et les coefficients de sécurité à utiliser pour les fondations et autres ouvrages en contact avec le sol.
Vérification du Non-Poinçonnement du Sol

D’autres exercices de Géotechnique :

0 commentaires
Soumettre un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *