Terrassement sur un Terrain Trapézoïdal
Comprendre le Terrassement sur un Terrain Trapézoïdal
Vous êtes ingénieur civil et vous devez préparer un plan de terrassement pour un nouveau développement résidentiel. Le terrain est un trapèze inégal avec une élévation variable. Votre tâche est de calculer le volume de terre à excaver et à remblayer pour préparer le site à la construction. Les spécifications et contraintes du projet nécessitent que le terrain soit nivelé à une élévation uniforme.
Pour comprendre l’Excavation de Terre pour un Parc Municipal, cliquez sur le lien.
Données fournies
- Dimensions du terrain (trapèze inégal):
- Longueur de la base supérieure: 50 m
- Longueur de la base inférieure: 70 m
- Hauteur: 30 m
- Élévations actuelles aux quatre coins:
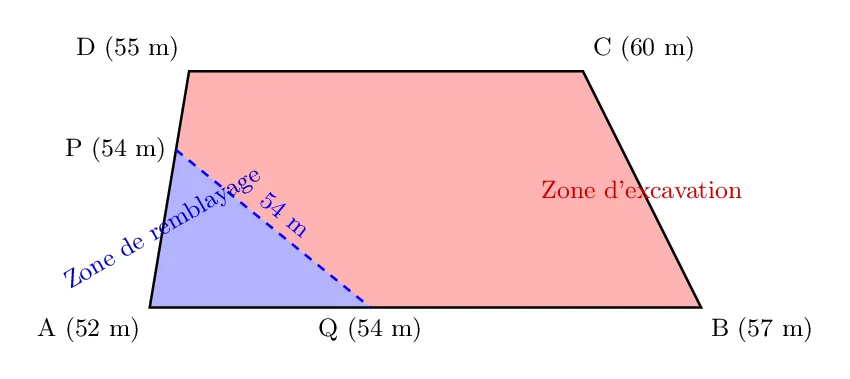
- Coin supérieur gauche: 55 m
- Coin supérieur droit: 60 m
- Coin inférieur gauche: 52 m
- Coin inférieur droit: 57 m
- Élévation souhaitée après terrassement: 54 m
- Densité moyenne de la terre: 1.5 tonnes/m³
- Type d’engin de terrassement disponible:
- Pelle mécanique avec une capacité de 0.8 m³ par pelletée
Questions :
1. Calculer le volume total de terre à excaver et à remblayer.
2. Estimer le nombre de pelletées nécessaires.
3. Déterminer le temps estimé pour l’opération de terrassement, en supposant que la pelle peut réaliser 20 pelletées par heure.
Correction : Terrassement sur un Terrain Trapézoïdal
1. Calcul du volume total de terre à excaver et à remblayer
a) Détermination de l’aire du terrain
Le terrain a une forme de trapèze dont l’aire se calcule par :
\[ A = \frac{(B_1 + B_2)}{2} \times h \]
où
- \(B_1 = 50 \, \text{m}\) (longueur de la base supérieure)
- \(B_2 = 70 \, \text{m}\) (longueur de la base inférieure)
- \(h = 30 \, \text{m}\) (hauteur du trapèze)
On a donc :
\[ A = \frac{(50 + 70)}{2} \times 30 \] \[ A = \frac{120}{2} \times 30 \] \[ A = 60 \times 30 \] \[ A = 1800 \, \text{m}^2 \]
b) Calcul de la différence d’élévation moyenne
Les élévations actuelles aux coins sont :
- Coin supérieur gauche : \(55 \, \text{m}\)
- Coin supérieur droit : \(60 \, \text{m}\)
- Coin inférieur gauche : \(52 \, \text{m}\)
- Coin inférieur droit : \(57 \, \text{m}\)
L’élévation moyenne actuelle est :
\[ \text{Élévation moyenne} = \frac{55 + 60 + 52 + 57}{4} \] \[ \text{Élévation moyenne} = \frac{224}{4} = 56 \, \text{m} \]
L’élévation souhaitée après terrassement est de \(54 \, \text{m}\).
La différence moyenne à corriger est donc :
\[ \Delta h = 56 – 54 = 2 \, \text{m} \]
c) Calcul du volume total à déplacer
En supposant que la variation d’élévation s’exprime de façon linéaire sur le terrain, le volume total de terre à excaver (dans les zones au-dessus de \(54 \, \text{m}\)) et à remblayer (dans les zones en dessous de \(54 \, \text{m}\)) est donné par :
\[ V = A \times \Delta h \] \[ V = 1800 \, \text{m}^2 \times 2 \, \text{m} \] \[ V = 3600 \, \text{m}^3 \]
2. Estimation du nombre de pelletées nécessaires
La pelle mécanique utilisée a une capacité de \(0,8 \, \text{m}^3\) par pelletée.
Le nombre de pelletées nécessaires est donc :
\[ N = \frac{V}{\text{capacité par pelletée}} \] \[ N = \frac{3600 \, \text{m}^3}{0,8 \, \text{m}^3} = 4500 \, \text{pelletées} \]
3. Détermination du temps estimé pour l’opération de terrassement
On suppose que la pelle peut réaliser 20 pelletées par heure.
Le temps total de travail est :
\[ T = \frac{N}{\text{pelletées par heure}} \] \[ T = \frac{4500}{20} = 225 \, \text{heures} \]
Récapitulatif
1. Volume total de terre à déplacer : \(3600 \, \text{m}^3\)
2. Nombre de pelletées nécessaires : \(4500 \, \text{pelletées}\)
3. Temps estimé pour l’opération : \(225 \, \text{heures}\)
Terrassement sur un Terrain Trapézoïdal
D’autres exercices de terrassement:















0 commentaires