Section d’une structure en bois
Comprendre la section d’une structure en bois
Vous êtes ingénieur(e) en génie civil avec une spécialisation en calcul de structures en bois. Au sein d’un bureau d’études, vous êtes chargé(e) de concevoir une poutre en bois de pin sylvestre capable de supporter une charge concentrée pour un bâtiment d’un étage.
Objectif:
Concevoir une poutre en pin sylvestre, en respectant les normes et contraintes de charge, pour garantir la stabilité et la sécurité du bâtiment.
Données Techniques:
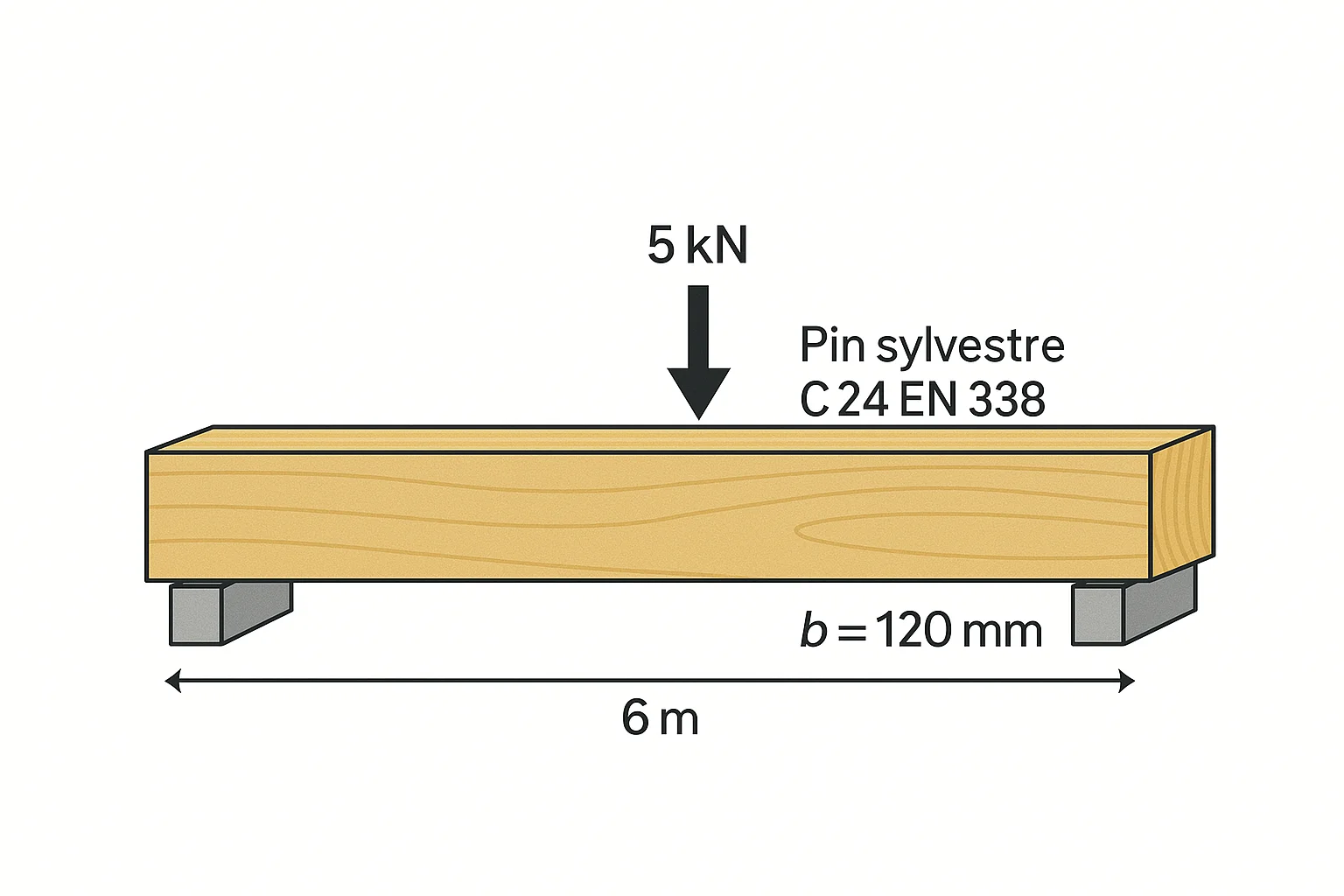
- Charge concentrée : 5 kN
- Portée de la poutre : 6 m
- Espèce de bois : Pin sylvestre
- Classe de résistance : C24 EN 338
- Facteur de charge de service : 1,5
- Facteur de modification pour la durabilité : 1,0 (environnement intérieur sec)
Questions:
- Calcul de la Charge Ultime (RU)
- Utilisez la charge concentrée et le facteur de charge de service pour calculer la charge ultime que la poutre doit supporter.
- Détermination du Moment Fléchissant Maximal (Mmax)
- Calculez le moment fléchissant maximal en utilisant la charge ultime et la portée de la poutre.
- Conception de la Section de la Poutre
- Déterminez la hauteur nécessaire de la poutre pour résister au moment fléchissant maximal, en considérant la largeur de la poutre, la contrainte admissible du bois, et calculez ensuite la section de la poutre.
Données supplémentaires :
- La contrainte admissible (\(f\)) pour le pin sylvestre est de \(24 \, \text{N/mm}^2\).
- Largeur de poutre (\(b\)) de \(120 \, \text{mm}\).
Correction : section d’une structure en bois
1. Charge Ultime (RU)
Formule:
\[RU = \text{Charge concentrée} \times \text{Facteur de charge de service}\]
Calcul:
- Charge concentrée = \(5\, \text{kN}\)
- Facteur de charge de service = \(1.5\)
\[RU = 5\, \text{kN} \times 1.5 \] \[RU= 7.5\, \text{kN}\]
2. Moments Fléchissants Maximaux (Mmax)
Formule:
\[M_{max} = \frac{RU \times L}{4}\]
Calcul:
- \(RU = 7.5\, \text{kN}\) (converti en \(7,500\, \text{N}\) pour cohérence d’unités)
- \(L = 6\, \text{m}\) (converti en \(6,000\, \text{mm}\) pour cohérence d’unités)
\[ M_{max} = \frac{7,500\, \text{N} \times 6,000\, \text{mm}}{4} \] \[ M_{max} = 11,250,000\, \text{Nmm}\, (\text{ou}\, 11.25\, \text{kNm}) \]
3. Section de la Poutre
Calcul de la hauteur (\(h\)) nécessaire:
Formule:
\[h = \sqrt{\frac{6 \times M_{max}}{f \times b}}\]
- \(M_{max} = 11,250,000\, \text{Nmm}\)
- \(f = 24\, \text{N/mm}^2\) (contrainte admissible pour le pin sylvestre)
- \(b = 120\, \text{mm}\) (largeur de la poutre supposée)
\[h = \sqrt{\frac{6 \times 11,250,000}{24 \times 120}}\] \[h = 153.09\, \text{mm}\]
Section de la poutre (\(S\)):
Formule:
\[S = b \times h\]
\[S = 120\, \text{mm} \times 153.09\, \text{mm} \] \[S = 18,371.17\, \text{mm}^2\, (\text{ou}\, 183.71\, \text{cm}^2)\]
Discussion:
La correction de l’exercice met en évidence l’importance d’une évaluation précise des forces agissant sur une structure et la nécessité d’une conception adéquate pour garantir la sécurité et la stabilité.
Les résultats obtenus montrent que la charge ultime (RU) et le moment fléchissant maximal (Mmax) sont correctement calculés.
La hauteur nécessaire de la poutre est bien plus importante que l’estimation initiale, ce qui indique le besoin d’une section transversale plus grande pour répondre aux exigences de charge et de sécurité.
Section d’une structure en bois
D’autres exercices de structure en bois:
0 commentaires