Réactions d’Appui et Efforts Internes
Comprendre les Réactions d’Appui et Efforts Internes
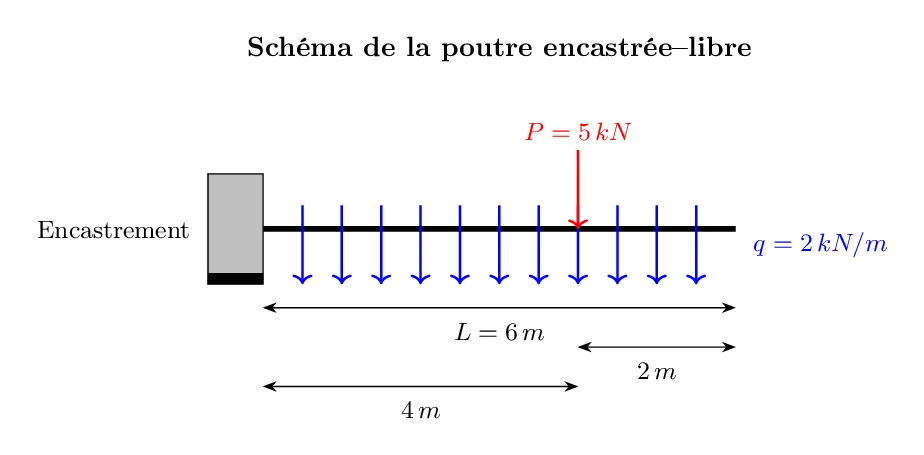
Considérons une poutre encastrée-libre d’une longueur . La poutre est soumise à une charge uniformément répartie sur toute sa longueur, ainsi qu’à une charge ponctuelle appliquée à de l’extrémité libre de la poutre.
Pour comprendre le Diagrammes d’Effort Tranchant et Moment et le calcul du Déplacement de l’Extrémité Libre d’une poutre, cliquez sur les liens.
Questions:
- Calculer les réactions d’appui à l’encastrement (à savoir, la réaction verticale (\(R_y\)), la réaction horizontale (\(R_x\)), et le moment d’encastrement (\(M\))
- Dessiner les diagrammes de moments fléchissants, d’efforts tranchants, et d’efforts normaux pour la poutre, en utilisant les réactions calculées.
Correction : Réactions d’Appui et Efforts Internes
1. Calcul des Réactions d’Appui
1.1. Choix du Système et Conventions
- On prend un repère le long de la poutre avec l’axe \(x\) orienté de l’encastrement (\(x=0\)) vers l’extrémité libre (\(x=6\)).
- Les charges \(q\) et \(P\) sont verticales (vers le bas).
- On adopte la convention suivante pour les moments : un moment qui tend à faire tourner la poutre dans le sens horaire est négatif.
1.2. Réaction Horizontale \(R_x\)
Aucune force horizontale n’étant appliquée, on a immédiatement :
\[ R_x = 0\;\text{kN}. \]
1.3. Réaction Verticale \(R_y\)
En appliquant l’équilibre vertical (somme des forces verticales nulle) :
\[ \Sigma F_y = 0 \quad\Longrightarrow\quad R_y – \underbrace{qL}_{\text{charge répartie}} – \underbrace{P}_{\text{charge ponctuelle}} = 0. \]
Calculons :
\[ qL = 2\;\text{kN/m} \times 6\;\text{m} = 12\;\text{kN}, \]
donc :
\[ R_y = 12\;\text{kN} + 5\;\text{kN} = 17\;\text{kN}. \]
Ainsi,
\[ R_y = 17\;\text{kN}\quad \text{(vers le haut)}. \]
1.4. Moment d’Encastrement \(M\)
En prenant les moments par rapport au point d’encastrement (\(x=0\)), la somme des moments doit être nulle :
\[ \Sigma M_{0} = 0 \quad\Longrightarrow\quad M + \left(\text{moments des charges}\right) = 0. \]
Calculons les moments (tous tendant à provoquer une rotation horaire, c’est-à-dire négatifs) :
1. Charge Uniformément Répartie \(q\) :
- Force totale : \(F_q = qL = 12\;\text{kN}\).
- Point d’application : centre de la poutre, soit à \(x = \frac{L}{2} = 3\;\text{m}\).
Moment :
\[ M_q = F_q \times 3\;\text{m} \] \[ M_q = 12 \times 3 \] \[ M_q = 36\;\text{kN}\cdot\text{m}. \]
2. Charge Ponctuelle \(P\) :
- Appliquée à \(x = 4\;\text{m}\).
Moment :
\[ M_P = P \times 4\;\text{m} \] \[ M_P = 5 \times 4 \] \[ M_P = 20\;\text{kN}\cdot\text{m}. \]
La somme des moments dus aux charges (sens horaire) est donc :
\[ M_q + M_P = 36 + 20 = 56\;\text{kN}\cdot\text{m}. \]
Pour l’équilibre des moments, le moment d’encastrement doit compenser ces moments :
\[ M – 56 = 0 \quad\Longrightarrow\quad M = 56\;\text{kN}\cdot\text{m}. \]
En d’autres termes, le moment d’encastrement est dirigé dans le sens anti–horaire pour compenser les moments horaires des charges.
Nous avons donc :
\[ M = 56\;\text{kN}\cdot\text{m}. \]
2. Diagrammes des Efforts Internes
Nous allons maintenant déterminer les expressions des diagrammes le long de la poutre en posant \(x\) mesuré à partir de l’encastrement (\(x = 0\)).
2.1. Diagramme de l’Effort Normal \(N(x)\)
Aucune force axiale n’étant appliquée, il n’existe pas d’effort normal dans la poutre :
\[ N(x) = 0 \quad\text{pour } 0 \le x \le 6. \]
2.2. Diagramme de l’Effort Tranchant \(V(x)\)
Pour déterminer \(V(x)\), on effectue l’équilibre des forces verticales sur une portion de poutre de \(x=0\) à un point \(x\).
Cas 1 : Pour \(0 \le x < 4\) (avant la charge ponctuelle)
Sur l’intervalle \([0,x]\) (avec \(x<4\)), seule la charge répartie intervient en plus de \(R_y\). La charge répartie sur cette portion est :
\[ \text{Charge répartie sur } [0,x] = qx = 2x\;\text{kN} \quad (\text{vers le bas}). \]
L’équilibre vertical donne alors :
\[ V(x) = R_y – qx = 17 – 2x. \]
Vérification :
- À \(x=0\) : \(V(0)=17\;\text{kN}\).
- Juste avant \(x=4\) : \(V(4^-)=17 – 2\times4 = 17 – 8 = 9\;\text{kN}\).
Cas 2 : Pour \(4 \le x \le 6\) (après la charge ponctuelle)
Pour \(x\) dépassant \(4\;\text{m}\), la charge ponctuelle \(P\) s’ajoute à la charge répartie. La somme des charges appliquées sur \([0,x]\) est alors :
\[ \text{Charge répartie} = 2x\;\text{kN}, \quad \text{et} \quad \text{charge ponctuelle } = 5\;\text{kN}. \]
L’équilibre vertical devient :
\[ V(x) = R_y – (qx + P) \] \[ V(x) = 17 – (2x + 5) \] \[ V(x) = 12 – 2x. \]
Vérification :
- Juste après \(x=4\) : \(V(4^+)=12 – 2\times4 = 12 – 8 = 4\;\text{kN}\).
- À \(x=6\) : \(V(6)=12 – 2\times6 = 12 – 12 = 0\;\text{kN}\), ce qui est attendu à l’extrémité libre.
Récapitulatif de \(V(x)\) :
\[ V(x)=
\begin{cases}
17 – 2x, & \text{pour } 0 \le x < 4,\\[1mm]
12 – 2x, & \text{pour } 4 \le x \le 6.
\end{cases}\]
Remarque : On observe une chute instantanée de \(5\;\text{kN}\) au point \(x=4\) (de \(9\;\text{kN}\) à \(4\;\text{kN}\)), correspondant à l’application de la charge ponctuelle.
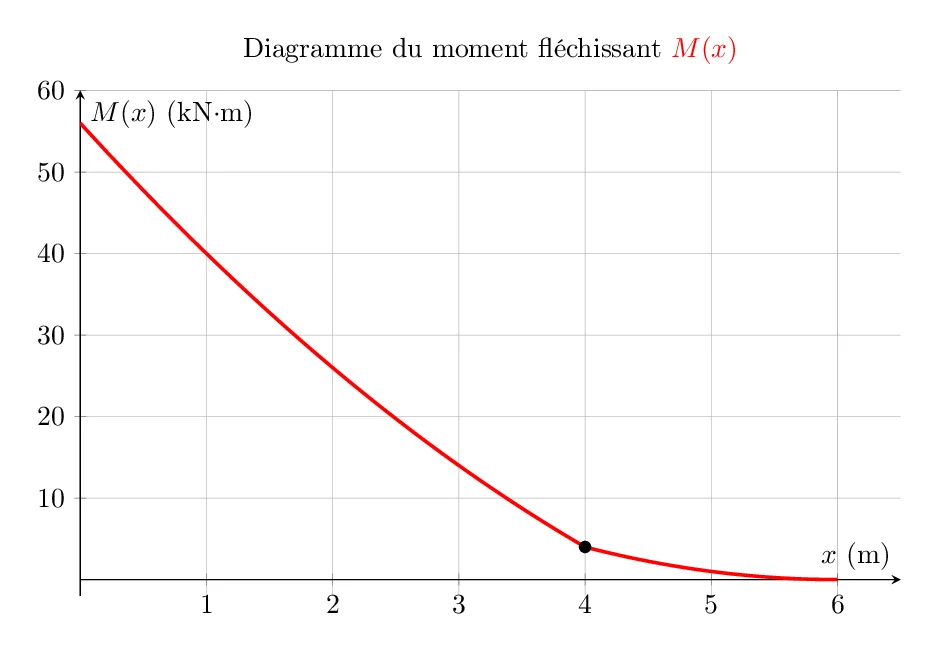
2.3. Diagramme de Moment Fléchissant \(M(x)\)
La relation entre le moment fléchissant et l’effort tranchant est donnée par :
\[ \frac{dM(x)}{dx} = -V(x). \]
Nous intégrons cette relation en connaissant la condition à l’encastrement :
\[ M(0) = M = 56\;\text{kN}\cdot\text{m}. \]
Cas 1 : Pour \(0 \le x < 4\)
On a :
\[ M(x) = M(0) – \int_{0}^{x} V(s)\,ds \] \[ M(x) = 56 – \int_{0}^{x} (17 – 2s)\,ds. \]
Calculons l’intégrale :
\[ \int_{0}^{x} (17 – 2s)\,ds = 17x – \int_{0}^{x} 2s\,ds = 17x – \left[ s^2 \right]_{0}^{x} = 17x – x^2. \]
D’où :
\[ M(x) = 56 – (17x – x^2) \] \[ M(x) = 56 – 17x + x^2. \]
Vérification :
- À \(x=0\) : \(M(0)=56\;\text{kN}\cdot\text{m}\).
- À \(x=4\) : \(M(4)=56 – 17\times4 + 4^2 = 56 – 68 + 16 = 4\;\text{kN}\cdot\text{m}\).
Cas 2 : Pour \(4 \le x \le 6\)
Pour \(x\ge 4\), on part de \(M(4)=4\;\text{kN}\cdot\text{m}\) et on intègre \(V(x)\) sur l’intervalle \([4,x]\) où \(V(s)=12 – 2s\) :
\[ M(x) = M(4) – \int_{4}^{x} (12 – 2s)\,ds. \]
Calculons l’intégrale :
\[ \int_{4}^{x} (12 – 2s)\,ds = \left[ 12s – s^2 \right]_{4}^{x} = (12x – x^2) – (12\times4 – 4^2). \]
Calculons la constante :
\[ 12\times4 – 4^2 = 48 – 16 = 32. \]
Donc :
\[ \int_{4}^{x} (12 – 2s)\,ds = 12x – x^2 – 32. \]
Ainsi,
\[ M(x) = 4 – (12x – x^2 – 32) \] \[ M(x) = 4 – 12x + x^2 + 32 \] \[ M(x) = 36 – 12x + x^2. \]
Vérification :
- À \(x=6\) : \(M(6)=36 – 12\times6 + 6^2 = 36 – 72 + 36 = 0\;\text{kN}\cdot\text{m}\), ce qui est cohérent à l’extrémité libre.
Récapitulatif de \(M(x)\) :
\[ M(x)=
\begin{cases}
56 – 17x + x^2, & \text{pour } 0 \le x < 4,\\[1mm]
36 – 12x + x^2, & \text{pour } 4 \le x \le 6.
\end{cases} \]
Réactions d’Appui et Efforts Internes

Réactions d’Appui et Efforts Internes
D’autres exercices de Rdm:















0 commentaires