Pressions de Terre au Repos et en Mouvement
Comprendre les Pressions de Terre au Repos et en Mouvement
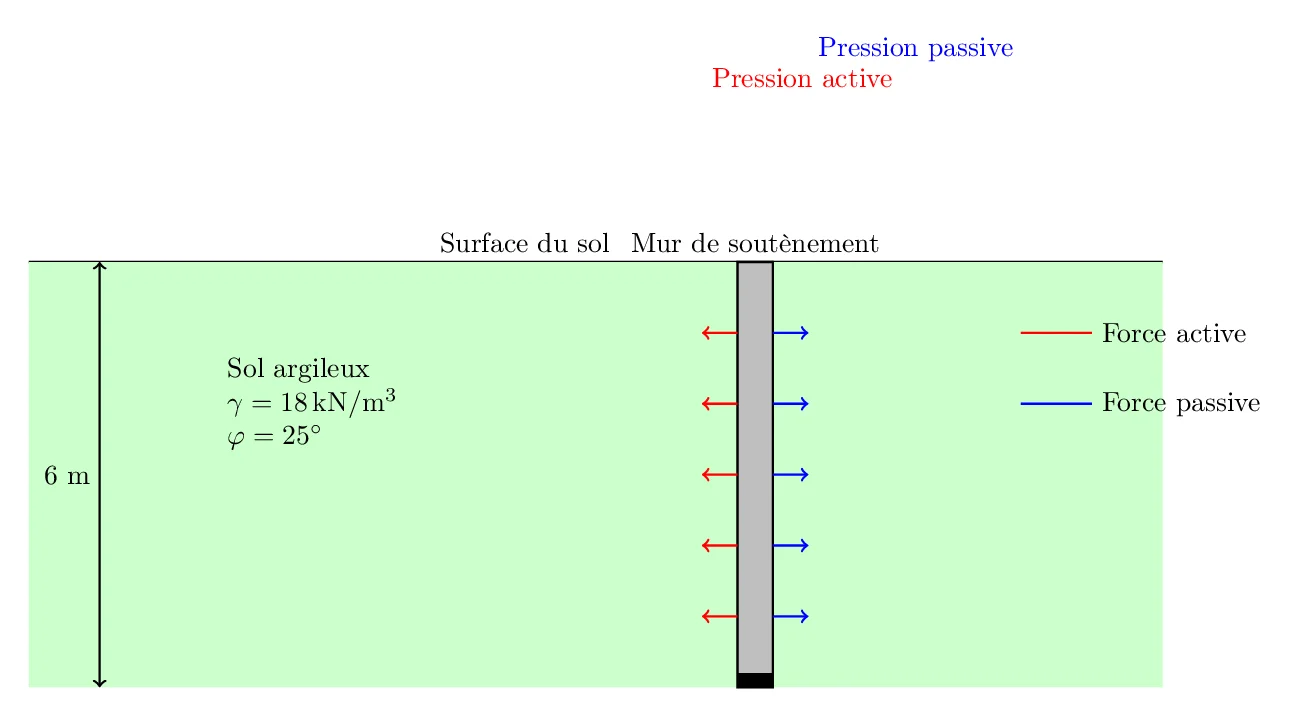
Vous êtes chargé de concevoir un mur de soutènement pour une tranchée de 6 mètres de profondeur destinée à l’installation de conduites souterraines. Le sol est argileux, avec les caractéristiques suivantes :
- Poids volumique du sol (\(\gamma\)) : 18 kN/m\(^3\)
- Angle de frottement interne (\(\phi\)) : 25\(^\circ\)
Questions:
1. Pression au Repos (\(P_0\))
- Calculez la pression au repos sur le mur de soutènement.
2. Pression Active (\(P_a\))
- Déterminez la pression active exercée sur le mur en utilisant la formule de Rankine.
- Calculez ensuite la force totale active (\(F_a\)) qui agit sur le mur et indiquez à quelle hauteur du bas du mur cette force est appliquée.
3. Pression Passive (\(P_p\))
- Évaluez la pression passive potentielle en utilisant également la formule de Rankine.
- Déterminez la force totale passive (\(F_p\)) et précisez la position de son point d’application sur le mur.
4. Discussion
- Discutez l’importance de connaître les pressions au repos, actives et passives pour la conception et la construction de murs de soutènement.
- Expliquez comment ces pressions influencent les décisions en matière de dimensionnement et de choix des matériaux pour le mur.
Correction : Pressions de Terre au Repos et en Mouvement
1. Calcul de la Pression au Repos (\(P_0\))
La pression au repos représente la pression latérale exercée par le sol sur le mur lorsque celui-ci ne subit aucune déplacement. Pour un sol normalement consolidé, le coefficient de pression au repos (\(k_0\)) se calcule généralement par la relation :
\[ k_0 = 1 – \sin(\varphi) \]
Ce coefficient traduit l’état initial de stress dans le sol avant toute action mobilisant le frottement interne.
Formule
La pression au repos à une profondeur \(z\) s’exprime par :
\[ P_0 = k_0 \times \gamma \times z \]
où :
- \(\gamma\) est le poids volumique du sol,
- \(z\) est la profondeur considérée.
Données
- Poids volumique, \(\gamma = 18\) kN/m\(^3\)
- Profondeur maximale de la tranchée, \(z = 6\) m
- Angle de frottement interne, \(\varphi = 25^\circ\)
Calcul
1. Calcul de \(k_0\) :
\[ k_0 = 1 – \sin(25^\circ) \]
Comme \(\sin(25^\circ) \approx 0,4226\), alors :
\[ k_0 = 1 – 0,4226 \] \[ k_0 = 0,5774 \]
2. Substitution dans la formule de \(P_0\) :
\[ P_0 = 0,5774 \times 18 \, \text{kN/m}^3 \times 6 \, \text{m} \] \[ P_0 = 0,5774 \times 108 \] \[ P_0 \approx 62,38 \, \text{kPa} \]
Résultat
La pression au repos à la base du mur est d’environ 62,38 kPa.
2. Calcul de la Pression Active (\(P_a\)) et de la Force Totale Active (\(F_a\))
La pression active correspond à la pression exercée sur le mur lorsqu’il se déplace légèrement vers l’arrière, mobilisant ainsi une partie du frottement interne. Selon la théorie de Rankine, le coefficient de pression active (\(k_a\)) se calcule par :
\[ k_a = \tan^2\left(45^\circ – \frac{\varphi}{2}\right) \]
Ce coefficient permet de déterminer la pression latérale variant linéairement avec la profondeur.
Formule
- Pression à une profondeur \(z\) :
\[ P_a(z) = k_a \times \gamma \times z \]
- La force totale active sur la hauteur \(H\) du mur (ici \(H = 6\) m) s’obtient par intégration de cette distribution linéaire :
\[ F_a = \frac{1}{2} \times k_a \times \gamma \times H^2 \]
Le point d’application de \(F_a\) se trouve à une hauteur égale à \(H/3\) mesurée à partir de la base (car la distribution de pression est triangulaire).
Données
- \(\varphi = 25^\circ\)
- \(\gamma = 18\) kN/m\(^3\)
- \(H = 6\) m
Calcul
1. Calcul de \(k_a\) :
\[ k_a = \tan^2\left(45^\circ – \frac{\varphi}{2}\right) \]
Pour \(\varphi = 25^\circ\), \(\frac{\varphi}{2} = 12,5^\circ\) et donc :
\[ 45^\circ – 12,5^\circ = 32,5^\circ \]
- \(\tan(32,5^\circ) \approx 0,636\) (valeur approchée)
Ainsi,
\[ k_a = (0,636)^2 \approx 0,404 \]
2. Pression active à la base (\(z = H = 6\) m) :
\[ P_a = k_a \times \gamma \times H = 0,404 \times 18 \times 6 \] \[ P_a \approx 0,404 \times 108 \] \[ P_a \approx 43,63 \, \text{kPa} \]
3. Force totale active (\(F_a\)) :
\[ F_a = \frac{1}{2} \times k_a \times \gamma \times H^2 \] \[ F_a = 0.5 \times 0.404 \times 18 \times 36 \] \[ F_a \approx 0.202 \times 648 \] \[ F_a \approx 130,90 \, \text{kN/m} \]
4. Point d’application de \(F_a\) :
Le résultat de la force active s’applique à \(H/3\) depuis la base, c’est-à-dire :
\[ H/3 = \frac{6}{3} = 2 \, \text{m} \]
Résultats
-
Pression active à la base : environ 43,63 kPa
-
Force totale active : environ 130,90 kN/m
-
Point d’application de Fₐ : à 2 m du bas du mur
3. Calcul de la Pression Passive (\(P_p\)) et de la Force Totale Passive (\(F_p\))
La pression passive intervient lorsque le mur se déplace vers l’avant, mobilisant une résistance plus importante due au frottement et à la densité du sol. Selon Rankine, le coefficient de pression passive (\(k_p\)) est donné par :
\[ k_p = \tan^2\left(45^\circ + \frac{\varphi}{2}\right) \]
Ce coefficient est généralement supérieur à \(k_a\), traduisant une plus grande résistance du sol en compression.
Formule
- Pression à une profondeur \(z\) :
\[ P_p(z) = k_p \times \gamma \times z \]
- La force totale passive sur la hauteur \(H\) est :
\[ F_p = \frac{1}{2} \times k_p \times \gamma \times H^2 \]
- Le point d’application de \(F_p\), comme pour la pression active, se trouve à \(H/3\) à partir de la base.
Données
- \(\varphi = 25^\circ\)
- \(\gamma = 18\) kN/m\(^3\)
- \(H = 6\) m
Calcul
1. Calcul de \(k_p\) :
\[ k_p = \tan^2\left(45^\circ + \frac{\varphi}{2}\right) \]
Pour \(\varphi = 25^\circ\), \(\frac{\varphi}{2} = 12,5^\circ\) et donc :
\[ 45^\circ + 12,5^\circ = 57,5^\circ \]
- \(\tan(57,5^\circ) \approx 1,539\) (valeur approchée)
Ainsi,
\[ k_p = (1,539)^2 \approx 2,37 \]
2. Pression passive à la base (\(z = H = 6\) m) :
\[ P_p = k_p \times \gamma \times H \] \[ P_p = 2,37 \times 18 \times 6 \] \[ P_p \approx 2,37 \times 108 \] \[ P_p \approx 255,96 \, \text{kPa} \]
3. Force totale passive (\(F_p\)) :
\[ F_p = \frac{1}{2} \times k_p \times \gamma \times H^2 \]
\(H^2 = 36\), alors :
\[ F_p = 0.5 \times 2,37 \times 18 \times 36 \] \[ F_p \approx 1,185 \times 648 \] \[ F_p \approx 768,38 \, \text{kN/m} \]
4. Point d’application de \(F_p\) :
Comme pour la force active, le résultat s’applique à \(H/3\) depuis la base, soit :
\[ H/3 = \frac{6}{3} = 2 \, \text{m} \]
Résultats
-
Pression passive à la base : environ 255,96 kPa
-
Force totale passive : environ 768,38 kN/m
-
Point d’application de Fₚ : à 2 m du bas du mur
4. Discussion
Importance des Pressions au Repos, Actives et Passives
-
Conception et Sécurité :
Connaître les pressions exercées par le sol sur le mur est essentiel pour assurer la stabilité de la structure. Le mur doit être dimensionné pour résister aux pressions actives qui tendent à le faire basculer et aux pressions passives qui offrent une résistance complémentaire en cas de déplacement vers l’avant. -
Dimensionnement :
-
Pression au repos (P₀) : Sert de base pour évaluer l’état naturel des contraintes dans le sol.
-
Pression active (Pₐ) : Permet de calculer la force de poussée sur le mur lorsqu’il se déplace légèrement vers l’arrière. Ce calcul aide à déterminer l’épaisseur, la base et l’armature nécessaires pour éviter le renversement.
-
Pression passive (Pₚ) : Indique la résistance du sol en cas de déplacement vers l’avant. Elle est utile pour vérifier que le mur ne subira pas un glissement sur son appui.
-
-
Choix des Matériaux :
La magnitude des pressions influe sur le choix des matériaux (béton, acier, etc.) ainsi que sur la forme et l’enrobage du mur de soutènement. Une bonne connaissance de ces pressions permet d’optimiser le rapport coût/sécurité et d’éviter des surdimensionnements inutiles ou des insuffisances structurelles. -
Sécurité en Cas de Charge Variable :
Dans des situations réelles, les charges peuvent varier (par exemple en présence d’eau ou suite à des variations de densité du sol). L’analyse des différentes pressions aide à concevoir un mur capable de résister à ces variations et ainsi prévenir des risques de défaillance structurelle.
Pressions de Terre au Repos et en Mouvement
D’autres exercices de géotechnique:














0 commentaires