Méthode de triangulation en topographie
Comprendre la méthode de triangulation en topographie
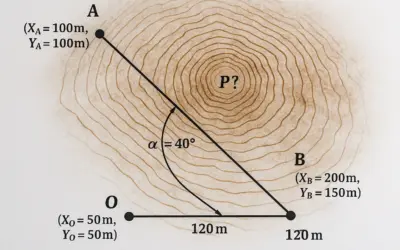
Vous êtes un ingénieur topographe travaillant sur un projet de construction d’une nouvelle route. Avant de commencer les travaux, vous devez effectuer un levé topographique pour déterminer la position exacte de trois points clés (A, B, C) sur le terrain. Vous décidez d’utiliser la méthode de triangulation pour cela.
Pour comprendre le Calcul de rayonnement à la station totale, cliquez sur le lien.
Données:
- Point de Base (P1): Coordonnées connues (100, 100).
- Distance P1-A: 150 mètres.
- Distance P1-B: 200 mètres.
- Angle entre P1-A et P1-B (α): 60 degrés.

Question :
Déterminer les coordonnées des points A, B, et C en utilisant la méthode de triangulation.
Correction : méthode de triangulation en topographie
1. Choix du repère et hypothèses
- Repère : On considère un repère cartésien dans lequel les axes sont définis comme suit :
– Axe \(x\) orienté vers l’est.
– Axe \(y\) orienté vers le nord. - Point de base : Le point \(P_1\) a des coordonnées connues \( (100\, ;\, 100) \).
- Hypothèse sur la direction :
Pour fixer le système, nous supposons que la direction de la station vers le point \(A\) correspond à \(0^\circ\) (c’est-à-dire horizontalement vers l’est).
Ensuite, l’angle mesuré entre les directions \(P_1A\) et \(P_1B\) est de \(60^\circ\), ce qui signifie que la direction \(P_1B\) fait un angle de \(60^\circ\) par rapport à l’axe positif \(x\).
2. Calcul des coordonnées du point \(A\)
Données pour \(A\) :
- Distance \(P_1\)–\(A\) : 150 m.
- Angle : \(0^\circ\) (par hypothèse).
Formules :
\[ x_A = x_{P_1} + d_{P_1A} \times \cos(\theta_A) \]
\[ y_A = y_{P_1} + d_{P_1A} \times \sin(\theta_A) \]
Calculs :
\[ x_A = 100 + 150 \times \cos(0^\circ) \]
\[\cos(0^\circ) = 1\]
donc,
\[ x_A = 100 + 150 \times 1 = 250 \]
\[ y_A = 100 + 150 \times \sin(0^\circ) \]
\[ \sin(0^\circ) = 0 \]
donc,
\[ y_A = 100 + 150 \times 0 = 100 \]
Résultat :
Les coordonnées du point \(A\) sont :
\[ A(250\, ;\, 100) \]
3. Calcul des coordonnées du point \(B\)
Données pour \(B\) :
- Distance \(P_1\)–\(B\) : 200 m.
- Angle : \(60^\circ\) (par rapport à la direction de \(P_1A\)).
Formules :
\[ x_B = x_{P_1} + d_{P_1B} \times \cos(60^\circ) \]
\[ y_B = y_{P_1} + d_{P_1B} \times \sin(60^\circ) \]
Calculs :
- Pour \(x_B\) :
\[ \cos(60^\circ) = 0.5 \]
donc,
\[ x_B = 100 + 200 \times 0.5 \] \[ x_B = 100 + 100 \] \[ x_B = 200 \]
- Pour \(y_B\) :
\[ \sin(60^\circ) = \frac{\sqrt{3}}{2} \approx 0.8660254 \]
donc,
\[ y_B = 100 + 200 \times 0.8660254 \] \[ y_B \approx 100 + 173.20508 \] \[ y_B = 273.20508 \]
Résultat :
Les coordonnées du point \(B\) sont :
\[ B(200\, ;\, 273.20508) \]
4. Discussion sur la détermination du point \(C\)
La méthode de triangulation permet de déterminer la position de plusieurs points en mesurant des distances et des angles. Dans cet exercice, nous disposons :
- D’un point de base \(P_1\) aux coordonnées connues.
- De deux distances mesurées depuis \(P_1\) (vers \(A\) et \(B\)).
- D’un angle de \(60^\circ\) entre les directions \(P_1A\) et \(P_1B\).
Analyse des données pour \(C\) :
Pour déterminer la position d’un troisième point \(C\) par triangulation, il est nécessaire de disposer d’au moins :
- Soit une distance mesurée (par exemple, \(A\)–\(C\) ou \(B\)–\(C\)),
- Soit d’un angle mesuré depuis \(A\) ou \(B\) (ou encore d’une intersection de directions issues de mesures prises sur le terrain).
Dans l’énoncé, aucune donnée supplémentaire (distance ou angle) relative à \(C\) n’est fournie.
Conclusion :
Avec les seules données disponibles, il est impossible de déterminer les coordonnées du point \(C\). On ne peut calculer que les coordonnées des points \(A\) et \(B\). Pour pouvoir localiser \(C\), il faudrait disposer d’informations complémentaires (par exemple, la distance \(A\)–\(C\) ou un angle mesuré à partir de \(A\) ou \(B\) vers \(C\)).
Méthode de triangulation en topographie
D’autres exercices de topographie:












0 commentaires