Mesure d’une Distance par Méthode Indirecte
Comprendre la Mesure d’une Distance par Méthode Indirecte
Vous êtes un topographe chargé de mesurer la distance entre deux points, A et B, situés de part et d’autre d’une rivière. Pour des raisons de sécurité, vous ne pouvez pas traverser la rivière directement.
Matériel Disponible
- Un théodolite placé en un point C, d’où vous pouvez voir les points A et B.
- Un ruban de mesure pour mesurer des distances courtes.
Opération sur le terrain:
1. Mesure d’une Base Accessible :
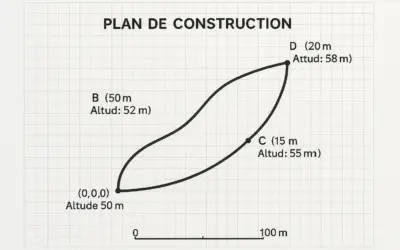
Trouvez un point D sur la même rive que C et mesurez la distance CD avec le ruban de mesure. Supposons que cette distance soit de 100 mètres.
2. Mesure des Angles :
À l’aide du théodolite, mesurez l’angle \(\angle DCA\) (notons cet angle \(\alpha\)) et l’angle \(\angle DCB\) (notons cet angle \(\beta\)). Supposons que \(\alpha = 50^\circ\) et \(\beta = 60^\circ\).
3. Calculs :
Utilisez la loi des sinus ou toute autre méthode appropriée pour calculer les distances CA et CB. Ensuite, calculez la distance AB, qui est la distance inconnue à mesurer.

Questions
A. Calculez les distances CA et CB en utilisant les données fournies.
B. Déterminez la distance AB.
Correction : Mesure d’une Distance par Méthode Indirecte
- Contexte : Vous êtes topographe. Vous voulez connaître la largeur de la rivière sans pouvoir la traverser.
- Point de départ : Le théodolite est installé au point \(C\) sur la rive.
- Base mesurable : \( CD = 100.0\ \mathrm{m} \). Cette distance est facile à mesurer car C et D sont sur la même rive.
- Angles observés :
- \( \alpha = 50^\circ \) : angle entre la direction \(CD\) et la ligne de visée vers le point \(A\) de l’autre rive.
- \( \beta = 60^\circ \) : angle entre la direction \(CD\) et la ligne de visée vers le point \(B\) de l’autre rive.
- Angle entre les directions : \( \theta = \beta - \alpha = 10^\circ \). Il représente l’angle au sommet du triangle \(A-C-B\).
A. Trouver les distances CA et CB
A.1. Déterminer CA
Objectif : Calculer la distance de C à A, notée \(CA\), sans pouvoir mesurer directement cette ligne, car elle traverse la rivière.
Pourquoi la loi des sinus ?
Imaginez un triangle formé par les points \(C\), \(D\) et \(A\). Nous connaissons un côté (\(CD\)) et deux angles à partir de \(C\) (\(\beta\) et \(\theta\)). La loi des sinus établit que, dans tout triangle :
“Le rapport d’un côté sur le sinus de l’angle opposé est le même pour tous les côtés.”
Formule :
Dans notre triangle :
\[ \frac{CA}{\sin(\beta)} = \frac{CD}{\sin(\theta)}. \]
En isolant \(CA\) :
\[ CA = CD \times \frac{\sin(\beta)}{\sin(\theta)}. \]
Données pour le calcul de CA :
- \(CD = 100.0\ \mathrm{m}\)
- \(\beta = 60^\circ\)
- \(\theta = 10^\circ\)
Calculs :
- Calculer les sinus :
- \(\sin(60^\circ) = 0.8660\)
- \(\sin(10^\circ) = 0.1736\) - Former le rapport :
\[ \frac{0.8660}{0.1736} \approx 4.9877 \] - Multiplier par la base :
\[ CA = 100.0 \times 4.9877 \approx 498.8\ \mathrm{m} \]
Résultat : \[ CA \approx 498.8\ \mathrm{m} \]
A.2. Déterminer CB
Objectif : Calculer la distance \(CB\) en formant le triangle \(C-D-B\).
Formule :
De la même façon :
\[ CB = CD \times \frac{\sin(\alpha)}{\sin(\theta)}. \]
Données pour CB :
- \(CD = 100.0\ \mathrm{m}\)
- \(\alpha = 50^\circ\)
- \(\theta = 10^\circ\)
Calculs :
- \(\sin(50^\circ) = 0.7660\) et \(\sin(10^\circ) = 0.1736\).
- \(0.7660 / 0.1736 \approx 4.4120\).
- \(CB = 100.0 \times 4.4120 \approx 441.2\ \mathrm{m}\).
Résultat : \[ CB \approx 441.2\ \mathrm{m} \]
B. Calculer la largeur AB
Objectif :
Maintenant que nous connaissons \(CA\) et \(CB\), et l’angle \(\theta\) entre eux, nous pouvons trouver la distance \(AB\), la largeur de la rivière.
Pourquoi la loi des cosinus ?
La loi des cosinus est une généralisation du théorème de Pythagore pour tout angle. Elle permet de relier trois côtés d’un triangle et l’angle entre deux d’entre eux :
\[ AB^2 = CA^2 + CB^2 - 2\,CA\,CB\,\cos(\theta). \]
Données pour AB :
- \(CA = 498.8\ \mathrm{m}\)
- \(CB = 441.2\ \mathrm{m}\)
- \(\theta = 10^\circ\)
- \(\cos(10^\circ) = 0.9848\)
Calculs :
- Calculer \(CA^2=(498.8)^2\approx248804\) et \(CB^2=(441.2)^2\approx194655\).
- Calculer le produit croisé :
\[ 2 \times 498.8 \times 441.2 \times 0.9848 \approx 433459 \] - Faire la somme et la différence :
\[ 248804 + 194655 - 433459 = 10000 \] - Extraire la racine carrée :
\[ AB = \sqrt{10000} = 100.0\ \mathrm{m} \]
Résultat : \[ AB = 100.0\ \mathrm{m} \]
Résumé des résultats
En une phrase : la rivière mesure \(100.0\ \mathrm{m}\) de large.
- \(CA \approx 498.8\ \mathrm{m}\)
- \(CB \approx 441.2\ \mathrm{m}\)
- \(AB = 100.0\ \mathrm{m}\)
Mesure d'une Distance par Méthode Indirecte
D’autres exercices de Topographie:








0 commentaires