Mesure de Distances, Angles et Altitudes
Comprendre la mesure de Distances, Angles et Altitudes
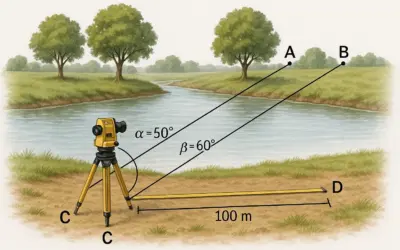
Vous êtes un ingénieur topographe travaillant sur un projet de construction d’un nouveau pont. Avant de commencer, vous devez effectuer un relevé topographique du site. Le site est un terrain relativement plat avec une légère inclinaison. Votre tâche consiste à mesurer la distance entre trois points de repère (A, B, C), calculer les angles formés par ces points et déterminer l’altitude de chacun.
Pour comprendre le Calcul de l’Angle au Sommet, cliquez sur le lien.
Données Fournies:
- Points de Repère:
- Point A (Point de départ)
- Point B (100 mètres à l’Est du point A)
- Point C (150 mètres au Nord-Est du point A sous un angle de 45° par rapport à la ligne AB)
- Altitude:
- Point A: 250 mètres au-dessus du niveau de la mer
- Inclinaison du terrain: 5° ascendant du point A vers le point C
- Instruments:
- Théodolite pour mesurer les angles
- Télémètre laser pour les distances
- Niveau numérique pour l’altitude

Questions:
1. Calcul de la Distance AC:
- Utilisez la méthode appropriée pour calculer la distance entre les points A et C.
2. Mesure des Angles:
- Déterminez l’angle ∠BAC en utilisant le théodolite.
- Calculez l’angle ∠ABC en considérant la géométrie du terrain.
3. Altitude des Points B et C:
- Calculez l’altitude du point B en considérant l’inclinaison du terrain.
- Déterminez l’altitude du point C en utilisant les données fournies et les calculs d’altitude.
Correction : mesure de Distances, Angles et Altitudes
1. Calcul de la Distance AC
Le point C est défini comme se trouvant à 150 mètres du point A, dans une direction faisant un angle de 45° par rapport à la ligne allant de A à B. On peut interpréter cette donnée de deux manières :
- Donnée directe : La distance horizontale AC est donnée comme étant 150 m.
- Calcul par coordonnées : En plaçant A à l’origine (0 ; 0), et sachant que l’angle de 45° implique que les composantes horizontales et verticales sont égales, on obtient pour C :
\[ x_C = 150 \times \cos(45°) \]
\[ y_C = 150 \times \sin(45°) \]
Formule et Calcul
1. Calcul des composantes
\[ \cos(45°) = \sin(45°) \approx 0.7071 \]
\[ x_C = 150 \times 0.7071 \approx 106.07 \, \text{m} \]
\[ y_C = 150 \times 0.7071 \approx 106.07 \, \text{m} \]
2. Calcul de la distance AC
En appliquant le théorème de Pythagore :
\[ AC = \sqrt{(x_C – 0)^2 + (y_C – 0)^2} \] \[ AC = \sqrt{(106.07)^2 + (106.07)^2} \] \[ AC = \sqrt{2 \times (106.07)^2} \] \[ AC \approx \sqrt{2 \times 11250} \] \[ AC \approx \sqrt{22500} \] \[ AC = 150 \, \text{m} \]
Résultat
Distance AC = 150 m
2. Mesure des Angles
2.1 Calcul de l’angle \(\angle BAC\)
L’angle ∠BAC est formé par les vecteurs AB et AC.
- Le vecteur AB va de A à B et, d’après les données, B est situé à 100 m à l’Est de A, soit :
\[ AB = (100, 0) \]
- Le vecteur AC est donné par les coordonnées de C que nous avons calculées :
\[ AC = (106.07, 106.07) \]
Le vecteur \(AC\) forme directement un angle de 45° avec l’axe des abscisses (la direction Est). Ainsi, l’angle entre AB (dirigé vers l’Est) et AC est de 45°.
Résultat
∠BAC = 45°
2.2 Calcul de l’angle \(\angle ABC\)
Pour calculer l’angle ∠ABC (angle en B), nous utilisons les vecteurs :
- BA : de B vers A
- BC : de B vers C
Coordonnées des points
- A : (0 ; 0)
- B : (100 ; 0)
- C : (106.07 ; 106.07)
Calcul des vecteurs
1. Vecteur BA
\[ BA = A – B \] \[ BA = (0 – 100, \, 0 – 0) \] \[ BA = (-100, \, 0) \]
2. Vecteur BC
\[ BC = C – B \] \[ BC = (106.07 – 100, \, 106.07 – 0) \] \[ BC = (6.07, \, 106.07) \]
Produit scalaire et normes
1. Produit scalaire de BA et BC
\[ BA \cdot BC = (-100) \times 6.07 + (0) \times 106.07 \] \[ = -607 \, \text{(arrondi)} \]
2. Norme de BA
\[ \|BA\| = \sqrt{(-100)^2 + 0^2} \] \[ \|BA\| = 100 \, \text{m} \]
3. Norme de BC
\[ \|BC\| = \sqrt{(6.07)^2 + (106.07)^2} \] \[ \|BC\| \approx \sqrt{36.85 + 11250} \] \[ \|BC\| \approx \sqrt{11286.85} \] \[ \|BC\| \approx 106.27 \, \text{m} \]
Formule de l’angle
La formule pour le cosinus de l’angle entre deux vecteurs est :
\[ \cos(\theta) = \frac{BA \cdot BC}{\|BA\| \times \|BC\|} \]
En substituant :
\[ \cos(\theta) = \frac{-607}{100 \times 106.27} \] \[ \cos(\theta) \approx \frac{-607}{10627} \] \[ \cos(\theta) \approx -0.0571 \]
Calcul de l’angle :
\[ \theta = \arccos(-0.0571) \] \[ \theta \approx 93.27° \, \text{(arrondi)} \]
Résultat
\(\angle ABC \approx 93.27°\)
3. Altitude des Points B et C
Le point A a une altitude de 250 m et le terrain présente une inclinaison de 5° dans la direction allant de A vers C. Pour déterminer l’altitude des points B et C, il faut calculer le gain d’altitude en fonction de la projection de la distance horizontale sur la direction de la pente.
Principe de Calcul
Pour une distance horizontale \(d\) parcourue dans la direction de la pente, le gain d’altitude est donné par :
\[ \Delta h = d \times \tan(5°) \]
Pour un point qui ne se trouve pas exactement dans la direction de la pente, on projette son déplacement sur la direction de la pente.
3.1 Altitude du Point B
Données
- Vecteur \(AB = (100,0)\)
- Direction de la pente (celle de AC) :
\[ u = (\cos(45°), \sin(45°)) \] \[ u \approx (0.7071, \, 0.7071) \]
- \( \tan(5°) \approx 0.08749 \)
Calcul de la Projection
La projection de \(AB\) sur la direction de la pente est obtenue par le produit scalaire :
\[ d_{proj} = AB \cdot u \] \[ d_{proj} = 100 \times 0.7071 + 0 \times 0.7071 \] \[ d_{proj} = 70.71 \, \text{m} \]
Calcul du Gain d’Altitude
\[ \Delta h_B = d_{proj} \times \tan(5°) \] \[ \Delta h_B = 70.71 \times 0.08749 \] \[ \Delta h_B \approx 6.19 \, \text{m} \]
Altitude du Point B
\[ h_B = h_A + \Delta h_B \] \[ h_B = 250 + 6.19 \] \[ h_B = 256.19 \, \text{m} \]
Résultat
Altitude du point B ≈ 256.19 m
3.2 Altitude du Point C
Données
La distance AC, qui est dans la direction de la pente, est \(150 \, \text{m}\).
Calcul du Gain d’Altitude
\[ \Delta h_C = AC \times \tan(5°) \] \[ \Delta h_C = 150 \times 0.08749 \] \[ \Delta h_C \approx 13.12 \, \text{m} \]
Altitude du Point C
\[ h_C = h_A + \Delta h_C \] \[ h_C = 250 + 13.12 \] \[ h_C = 263.12 \, \text{m} \]
Résultat
Altitude du point C ≈ 263.12 m
Récapitulatif Final
1. Distance AC :
-
- AC = 150 m
2. Angles Mesurés :
- ∠BAC = 45°
- ∠ABC ≈ 93.27°
3. Altitudes :
- Altitude du point B ≈ 256.19 m
- Altitude du point C ≈ 263.12 m
Mesure de Distances, Angles et Altitudes
D’autres exercices de Topographie:







0 commentaires