La loi de Hooke Exercice corrigé
Comprendre le calcul selon la loi de Hooke
Dans un laboratoire de mécanique, un ingénieur teste la résilience d’un ressort en acier. Il souhaite comprendre comment le ressort réagit sous différentes charges et jusqu’à quel point il peut être étiré sans dépasser sa limite élastique. Les mesures de base du ressort, sa raideur, et la limite élastique de l’acier sont connues. L’ingénieur effectue une série d’expériences pour déterminer l’allongement du ressort sous une force spécifique et la force maximale que le ressort peut supporter sans subir de déformation permanente.
Pour comprendre la Vérification de la limite d’élasticité, cliquez sur le lien.
Les caractéristiques sont les suivantes :
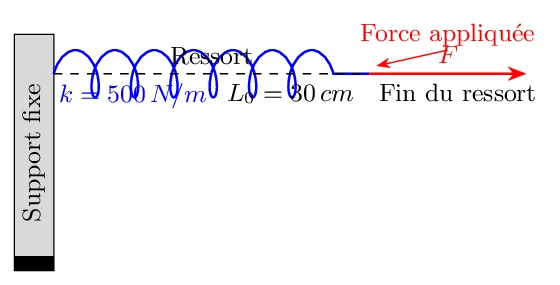
- Longueur initiale (non étirée) : \( L_0 = 30 \, \text{cm} \)
- Constante du ressort (raideur) : \( k = 500 \, \text{N/m} \)
- Limite élastique de l’acier : \( \sigma_{\text{lim}} = 250 \, \text{MPa} \)
- Section transversale du ressort : \( A = 1 \, \text{cm}^2 \)
Questions :
1. Déformation Élastique : Calculez la déformation élastique (allongement) du ressort lorsque vous appliquez une force de \( 100 \, \text{N} \).
2. Contrainte dans le Ressort : Déterminez la contrainte dans le ressort sous cette force de \( 100 \, \text{N} \). Comparez cette contrainte avec la limite élastique de l’acier pour vérifier si le ressort reste dans le domaine élastique.
3. Force Maximale : Quelle est la force maximale que l’on peut appliquer sur le ressort sans dépasser la limite élastique de l’acier ?
4. Allongement Maximal : Calculez l’allongement maximal du ressort sous cette force maximale en utilisant à nouveau la loi de Hooke.
Correction : la loi de Hooke
1. Déformation Élastique
Selon la loi de Hooke, la force appliquée sur un ressort est proportionnelle à son allongement. La relation s’exprime par :
\[ F = k \cdot \Delta L \]
Pour trouver l’allongement \(\Delta L\), on réarrange la formule :
\[ \Delta L = \frac{F}{k} \]
Données :
- Force appliquée, \(F = 100\,\text{N}\)
- Raideur du ressort, \(k = 500\,\text{N/m}\)
Calcul :
\[ \Delta L = \frac{100\,\text{N}}{500\,\text{N/m}} \] \[ \Delta L = 0,2\,\text{m} \]
Soit 20 cm d’allongement.
2. Contrainte dans le Ressort
La contrainte (\(\sigma\)) dans un matériau se calcule en divisant la force par la surface de la section transversale.
\[ \sigma = \frac{F}{A} \]
Données :
- Force appliquée, \(F = 100\,\text{N}\)
- Section transversale, \(A = 1\,\text{cm}^2 = 1 \times 10^{-4}\,\text{m}^2\)
Calcul :
\[ \sigma = \frac{100\,\text{N}}{1 \times 10^{-4}\,\text{m}^2} = 1 \times 10^6\,\text{Pa} \]
Soit 1 MPa.
Vérification :
La contrainte obtenue (1 MPa) est bien inférieure à la limite élastique de l’acier (σ_lim = 250 MPa), ce qui confirme que le ressort reste dans le domaine élastique.
3. Force Maximale Sans Dépasser la Limite Élastique
La force maximale que le ressort peut supporter sans dépasser la limite élastique est déterminée en égalant la contrainte maximale à la contrainte de la matière.
\[ F_{\text{max}} = \sigma_{\text{lim}} \cdot A \]
Données :
- Limite élastique de l’acier, \(\sigma_{\text{lim}} = 250\,\text{MPa} = 250 \times 10^6\,\text{Pa}\)
- Section transversale, \(A = 1\,\text{cm}^2 = 1 \times 10^{-4}\,\text{m}^2\)
Calcul :
\[ F_{\text{max}} = (250 \times 10^6\,\text{Pa}) \times (1 \times 10^{-4}\,\text{m}^2) \] \[ F_{\text{max}} = 25\,000\,\text{N} \]
4. Allongement Maximal du Ressort
En appliquant la loi de Hooke, l’allongement maximal associé à la force maximale \(F_{\text{max}}\) se calcule par :
\[ \Delta L_{\text{max}} = \frac{F_{\text{max}}}{k} \]
Données :
- Force maximale, \(F_{\text{max}} = 25\,000\,\text{N}\)
- Raideur du ressort, \(k = 500\,\text{N/m}\)
Calcul :
\[ \Delta L_{\text{max}} = \frac{25\,000\,\text{N}}{500\,\text{N/m}} = 50\,\text{m} \]
Conclusion
- Allongement pour F = 100 N : 0,2 m (20 cm)
- Contrainte correspondante : 1 MPa (inférieure à 250 MPa, donc élastique)
- Force maximale admissible : 25 000 N
- Allongement maximal sous F_max : 50 m
Ces résultats montrent que, bien que l’application de 100 N reste dans le domaine élastique, la force maximale calculée conduit à un allongement très important (50 m) ce qui, en pratique, mettrait en cause les hypothèses de validité de la loi de Hooke pour un tel étirement.
La loi de Hooke
D’autres exercices de Rdm :















0 commentaires