Formule RDM
La résistance des matériaux, souvent appelée RDM, est une discipline qui étudie le comportement des solides sous l’action des charges extérieures. Elle fournit des méthodes pour déterminer les contraintes, les déformations et les déplacements dans les structures. Voici un aperçu condensé des formules de RDM :
| Catégorie | Formule | Description |
|---|---|---|
| Tension / Compression | σ = F / A |
Contrainte normale (σ, en N/m² ou Pa) due à une force axiale F appliquée sur une section A. F : Force appliquée (N) A : Aire de la section (m²) |
| Déformation | ε = δ / L |
Déformation unitaire (ε) définie par le rapport de la variation de longueur δ à la longueur initiale L. δ : Allongement ou raccourcissement (m) L : Longueur initiale (m) |
| Loi de Hooke | σ = E · ε |
Relation élastique entre contrainte et déformation. E : Module d'Young (Pa) ε : Déformation unitaire (sans dimension) |
| Moment d'inertie | I = ∫ y² dA |
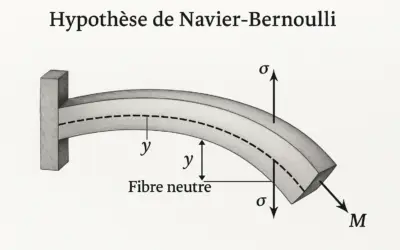
Calcul du moment d'inertie (I) d'une section par rapport à l'axe neutre. y : Distance par rapport à l'axe neutre (m) dA : Élément d'aire (m²) |
| Moment polaire d'inertie | J = ∫ (x² + y²) dA |
Calcul du moment polaire d'inertie (J) utilisé notamment en torsion. x et y : Coordonnées par rapport à l'axe de torsion (m) |
| Flexion - Contrainte | σ = (M · y) / I |
Contrainte normale induite par un moment de flexion M. M : Moment fléchissant (N·m) y : Distance à l'axe neutre (m) I : Moment d'inertie (m⁴) |
| Flexion - Flèche (poutre simplement appuyée) | δmax = (5 · q · L⁴) / (384 · E · I) |
Flèche maximale d'une poutre simplement appuyée soumise à une charge uniformément répartie. q : Intensité de la charge (N/m) L : Portée de la poutre (m) E : Module d'Young (Pa) I : Moment d'inertie (m⁴) |
| Flexion - Flèche (poutre en porte-à-faux) | δmax = (q · L⁴) / (8 · E · I) |
Flèche maximale d'une poutre en porte-à-faux soumise à une charge uniformément répartie. Les variables sont identiques à celles de la formule précédente. |
| Flexion - Flèche (charge ponctuelle) | δmax = (F · L³) / (48 · E · I) |
Flèche maximale d'une poutre simplement appuyée avec une charge concentrée F appliquée au centre. F : Charge ponctuelle (N) |
| Torsion - Contrainte | τ = (T · r) / J |
Contrainte de cisaillement due à un moment de torsion T sur une section. T : Moment de torsion (N·m) r : Rayon (m) ou distance maximale à l'axe J : Moment polaire d'inertie (m⁴) |
| Torsion - Angle de torsion | φ = (T · L) / (G · J) |
Angle de torsion (φ, en radians) pour une barre de longueur L soumise à un moment T. G : Module de rigidité (Pa) |
| Cisaillement | τ = (V · Q) / (I · b) |
Contrainte de cisaillement dans une section de poutre soumise à une force tranchante V. V : Force de cisaillement (N) Q : Premier moment d'aire (m³) de la zone située de part et d'autre de la fibre considérée b : Largeur à la fibre (m) |
| Flambement (Euler) | Fcr = (π² · E · I) / (K · L)² |
Charge critique de flambement d'une colonne. L : Longueur de la colonne (m) K : Coefficient d'appui (dépend des conditions aux limites, sans dimension) |
| Section circulaire | I = (π · d⁴) / 64 |
Moment d'inertie pour une section circulaire de diamètre d. d : Diamètre (m) |
| Section circulaire | J = (π · d⁴) / 32 |
Moment polaire d'inertie pour une section circulaire. Utilisé pour le calcul des contraintes en torsion. |
| Section rectangulaire | I = (b · h³) / 12 |
Moment d'inertie d'une section rectangulaire. b : Largeur (m) h : Hauteur (m) |
| Premier moment d'aire | Q = A' · y' |
Calcul du premier moment d'aire pour une portion de section (A') dont le centroïde est situé à une distance y' de l'axe neutre. Utile pour l'analyse de la distribution des contraintes de cisaillement. |
Formules complémentaires:
| Catégorie | Formule | Description |
|---|---|---|
| Moment-Courbure | κ = M / (E · I) |
Relation entre le moment fléchissant M et la courbure κ d'une poutre. M : Moment fléchissant (N·m) E : Module d'Young (Pa) I : Moment d'inertie (m⁴) |
| Énergie en flexion | U = ∫₀ᴸ [M(x)² / (2 · E · I)] dx |
Énergie de déformation stockée dans une poutre soumise à la flexion. M(x) : Moment fléchissant variable selon x L : Longueur de la poutre (m) |
| Calcul de flèche | δ(x) = ∫∫ [M(x) / (E · I)] dx² |
Méthode de double intégration pour déterminer la déformation (flèche) d'une poutre. Chaque intégrale tient compte des conditions aux limites. |
| Angle de rotation | θ(x) = ∫ [M(x) / (E · I)] dx |
Calcul de l'angle de rotation d'une poutre en flexion. Permet d'obtenir la pente de la déformation en un point x. |
| Sollicitations combinées | σ = (F / A) ± (M · y / I) |
Calcul de la contrainte résultante lorsqu'une section subit simultanément une force axiale F et un moment M. F : Force axiale (N) A : Aire de la section (m²) y : Distance par rapport à l'axe neutre (m) |
| Effort tranchant | V = dM/dx |
Relation entre le moment fléchissant et l'effort tranchant V dans une poutre. Dérivée du moment par rapport à la position x. |
| Énergie en torsion | U = ∫₀ᴸ [T(x)² / (2 · G · J)] dx |
Énergie stockée dans un élément soumis à la torsion. T(x) : Moment de torsion variable selon x G : Module de rigidité (Pa) J : Moment polaire d'inertie (m⁴) |
| Torsion (sections non circulaires) | τmax = T · c / Jt |
Estimation de la contrainte de torsion pour une section non circulaire. T : Moment de torsion (N·m) c : Distance maximale de la fibre à l'axe de torsion (m) Jt : Module de torsion adapté à la forme de la section |
Formules utilisées en Génie Civil
| Catégorie | Formule | Description |
|---|---|---|
| Poutre - Charge Uniformément Répartie | Mmax = (q · L²) / 8 |
Moment fléchissant maximal pour une poutre simplement appuyée soumise à une charge uniformément répartie. q : Intensité de la charge (N/m) L : Portée de la poutre (m) |
| Poutre - Encadrée / Encastrement | Mmax = (q · L²) / 12 |
Moment fléchissant maximal pour une poutre encastrée aux deux extrémités et soumise à une charge uniformément répartie. Les paramètres sont identiques à ceux de la formule précédente. |
| Flèche (Poutre simplement appuyée) | δmax = (5 · q · L⁴) / (384 · E · I) |
Flèche maximale d'une poutre simplement appuyée. E : Module d'Young (Pa) I : Moment d'inertie de la section (m⁴) |
| Colonne - Flambement | Fcr = (π² · E · I) / (K · L)² |
Charge critique de flambement pour une colonne. La valeur de K dépend des conditions d'appui. L : Longueur de la colonne (m) K : Coefficient d'appui (sans dimension) |
| Fondations | qult = c · Nc + q · Nq + 0.5 · γ · B · Nγ |
Capacité portante ultime d'une semelle, selon la formule de Terzaghi. c : Cohésion du sol (Pa) q : Pression effective (Pa) γ : Poids volumique du sol (N/m³) B : Largeur de la fondation (m) Nc, Nq, Nγ : Facteurs de capacité portante (sans dimension) |
| Matériaux (Béton) | Ec = 4700 · √(fck) |
Estimation du module d'élasticité du béton (Ec en MPa) en fonction de sa résistance caractéristique fck (MPa). Cette formule est indicative et peut varier selon les normes. |
| Matériaux (Acier) | σ = E · ε |
Loi de Hooke appliquée à l'acier, liant la contrainte σ (Pa) à la déformation ε. E : Module d'Young de l'acier (Pa) |
Formule Rdm
Exercices de Rdm :







Merci beaucoup j’ai aimé bien