Évaluer les propriétés mécaniques sols
Comprendre évaluer les propriétés mécaniques sols
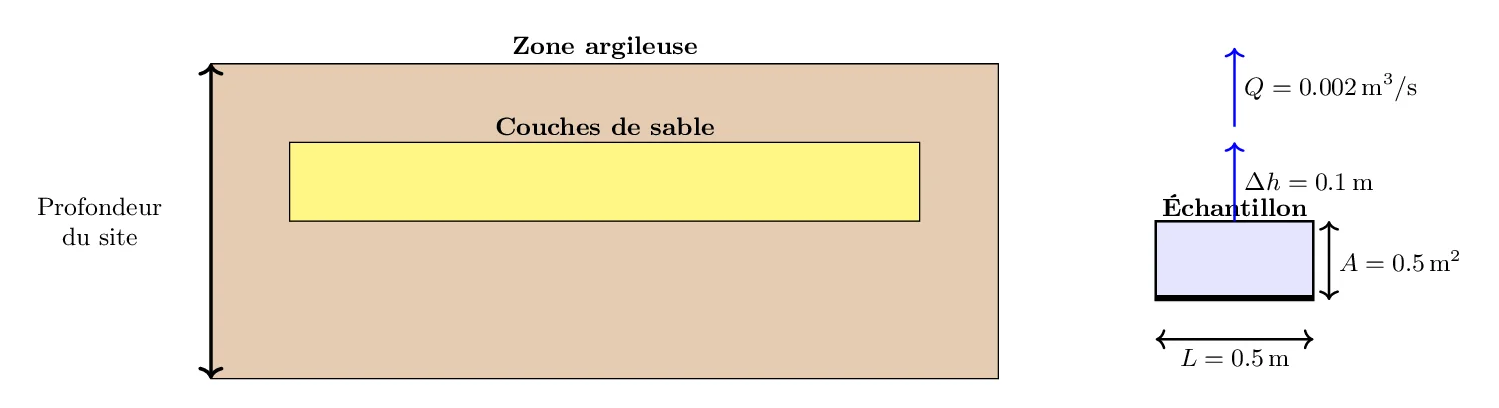
Un ingénieur géotechnique doit évaluer les propriétés mécaniques d’un sol pour un projet de construction. Le site est une zone argileuse avec des couches de sable.
Pour comprendre l’Évaluation des propriétés d’un sol, cliquez sur le lien.
Données
- Masse du sol (M): 1500 kg
- Volume du sol (V): 1 m³
- Volume des vides (Vv): 0.35 m³
- Débit d’eau (Q): 0.002 m³/s
- Surface de l’échantillon (A): 0.5 m²
- Différence de hauteur d’eau (Δh): 0.1 m
- Longueur de l’échantillon (L): 0.5 m
Questions
1. Calculer la densité du sol.
2. Déterminer la porosité du sol.
3. Estimer la perméabilité du sol.
4. En utilisant les résultats d’un test de cisaillement direct (cohésion \(c = 25 \, \text{kPa}\) et angle de frottement interne \(\phi = 30^\circ\)), évaluez la résistance au cisaillement du sol pour une contrainte effective \(\sigma’ = 100 \, \text{kPa}\).
Correction : évaluer les propriétés mécaniques sols
1. Calcul de la densité du sol
La densité (\(\rho\)) d’un sol se définit comme la masse totale du sol divisée par son volume total.
Formule :
\[ \rho = \frac{M}{V} \]
Données :
- Masse du sol, M = 1500 kg
- Volume du sol, V = 1 m³
Calcul :
\[ \rho = \frac{1500 \, \text{kg}}{1 \, \text{m}^3} = \mathbf{1500 \, \text{kg/m}^3} \]
2. Détermination de la porosité du sol
La porosité (\(n\)) est le rapport du volume des vides à celui du sol total. Elle est souvent exprimée en pourcentage.
Formule :
\[ n = \frac{V_v}{V} \]
Données :
- Volume des vides, Vv = 0.35 m³
- Volume du sol, V = 1 m³
Calcul :
\[ n = \frac{0.35 \, \text{m}^3}{1 \, \text{m}^3} = 0.35 \quad \text{soit} \quad \mathbf{35\%} \]
3. Estimation de la perméabilité du sol
La perméabilité (k) peut être estimée à l’aide de la loi de Darcy, qui relie le débit (Q) traversant une surface (A) à la différence de charge hydraulique (Δh) sur une longueur (L).
Formule (loi de Darcy) :
\[ Q = k \times A \times \frac{\Delta h}{L} \]
On peut isoler \(k\) :
\[ k = \frac{Q}{A \times (\Delta h / L)} = \frac{Q \times L}{A \times \Delta h} \]
Données :
- Débit d’eau, Q = 0.002 m³/s
- Surface de l’échantillon, A = 0.5 m²
- Différence de hauteur d’eau, Δh = 0.1 m
- Longueur de l’échantillon, L = 0.5 m
Calcul :
\[ k = \frac{0.002 \, \text{m}^3/\text{s} \times 0.5 \, \text{m}}{0.5 \, \text{m}^2 \times 0.1 \, \text{m}} \] \[ k = \frac{0.001 \, \text{m}^4/\text{s}}{0.05 \, \text{m}^3} \] \[ k = \mathbf{0.02 \, \text{m/s}} \]
4. Évaluation de la résistance au cisaillement du sol
La résistance au cisaillement (τ) d’un sol peut être estimée à partir des résultats d’un test de cisaillement direct. La relation utilisée est la loi de Coulomb, qui exprime la résistance au cisaillement comme la somme de la cohésion et de la composante frictionnelle due à la contrainte effective.
Formule (loi de Coulomb) :
\[ \tau = c + \sigma’ \times \tan(\phi) \]
Données :
- Cohésion, c = 25 kPa
- Angle de frottement interne, ϕ = 30°
- Contrainte effective, σ′ = 100 kPa
Calcul :
1. Calcul de \(\tan(\phi)\) :
\[ \tan(30^\circ) \approx 0.577 \]
2. Application de la formule :
\[ \tau = 25 \, \text{kPa} + 100 \, \text{kPa} \times 0.577 \] \[ \tau = 25 \, \text{kPa} + 57.7 \, \text{kPa} \] \[ \tau \approx \mathbf{82.7 \, \text{kPa}} \]
Résumé des résultats
- Densité du sol : 1500 kg/m³
- Porosité du sol : 35 %
- Perméabilité du sol : 0.02 m/s
- Résistance au cisaillement : 82.7 kPa
Évaluer les propriétés mécaniques sols
D’autres exercices de Géotechnique:









0 commentaires