Évaluation de la Capacité de Traction d’une Poutre

Comprendre l’Évaluation de la Capacité de Traction d’une Poutre

Un ingénieur en génie civil doit concevoir une poutre en acier pour supporter une charge uniformément répartie, incluant son propre poids, sur une portée libre. La poutre est supposée être simplement appuyée aux deux extrémités et soumise à une charge de traction due au poids des équipements qui y seront accrochés.

Comprendre les Contraintes et déformations en traction, cliquez sur le lien.

Données fournies:

• Matériau: Acier, avec une limite élastique de 250 MPa et un module d’élasticité de 200 GPa.
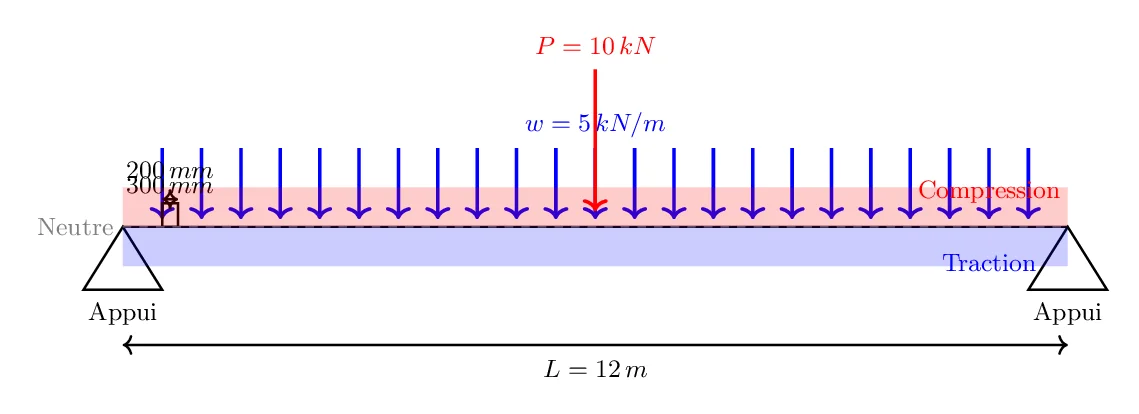
• Dimensions de la poutre: Longueur = 12 m, section transversale rectangulaire avec une largeur de 200 mm et une hauteur de 300 mm.
• Charge uniformément répartie (incluant le poids propre): 5 kN/m.
• Charge concentrée due aux équipements: 10 kN, appliquée au centre de la poutre.

Questions à résoudre:

1. Calcul du poids propre de la poutre:

• Utilisez la densité de l’acier (7850 kg/m³) pour calculer le poids propre de la poutre par mètre linéaire.
• Déduisez ensuite la charge totale due au poids propre sur toute la longueur de la poutre.

2. Calcul de la force de traction totale:

• Calculez la réaction aux appuis en considérant les charges uniformément réparties et la charge concentrée.
• Déterminez la force de traction dans la poutre due aux réactions aux appuis.

3. Vérification de la contrainte de traction maximale:

• Calculez la contrainte de traction maximale dans la poutre en utilisant la force de traction totale et la section transversale de la poutre.
• Comparez cette contrainte avec la limite élastique de l’acier pour vérifier si la poutre est adéquatement dimensionnée.

Correction : Évaluation de la Capacité de Traction d’une Poutre

1. Calcul du Poids Propre de la Poutre

a) Calcul de la masse linéique (par mètre)

Formule :

$$\text{Masse par mètre} = \rho \times A$$

avec l’aire de la section :

$$A = b \times h$$

Données :

• $b = 0,2\,\text{m}$
• $h = 0,3\,\text{m}$
• $A = 0,2 \times 0,3 = 0,06\,\text{m}^2$
• $\rho = 7850\,\text{kg/m}^3$

Calcul :

$$\text{Masse par mètre} = 7850 \times 0,06$$ $$\text{Masse par mètre} = 471\,\text{kg/m} \quad(\text{arrondi})$$

b) Conversion en Poids Linéique

Formule :

$$\text{Poids par mètre} = \text{Masse par mètre} \times g$$

Calcul :

$$= 471\,\text{kg/m} \times 9,81\,\text{m/s}^2$$ $$\approx 4623\,\text{N/m}$$ $$\approx 4,62\,\text{kN/m}$$

c) Charge Totale Due au Poids Propre

Formule :

$$\text{Charge totale} = \text{Poids par mètre} \times L$$

Calcul :

$$= 4,62\,\text{kN/m} \times 12\,\text{m}$$ $$\approx 55,44\,\text{kN}$$

Remarque : Dans l’énoncé, la charge uniformément répartie $5\,\text{kN/m}$ inclut déjà le poids propre. Ici, nous avons isolé le seul poids propre qui représente environ $4,62\,\text{kN/m}$ (soit $55,44\,\text{kN}$ sur toute la longueur).

2. Calcul de la Force de Traction Totale

L’évaluation de la « force de traction » dans la poutre consiste à :

• (a) Calculer les réactions aux appuis
• (b) Déterminer le moment fléchissant maximum
• (c) En déduire la contrainte (et, par intégration, la force résultante dans la zone tendue)

2.a) Réactions aux Appuis

Pour une poutre simplement appuyée, les charges verticales se répartissent également entre les deux appuis.

1. Charge Uniformément Répartie (UDL) :

• Charge totale due à la UDL :

$$W_{\text{UDL}} = w \times L$$ $$W_{\text{UDL}} = 5\,\text{kN/m} \times 12\,\text{m}$$ $$W_{\text{UDL}} = 60\,\text{kN}$$

• Réaction à chaque appui (UDL seule) :

$$R_{\text{UDL}} = \frac{60\,\text{kN}}{2} = 30\,\text{kN}$$

2. Charge Concentrée :

• Réaction à chaque appui :

$$R_{\text{point}} = \frac{P}{2} = \frac{10\,\text{kN}}{2} = 5\,\text{kN}$$

3. Réaction Totale à Chaque Appui :

$$R_{\text{total}} = R_{\text{UDL}} + R_{\text{point}}$$ $$R_{\text{total}} = 30\,\text{kN} + 5\,\text{kN}$$ $$R_{\text{total}} = 35\,\text{kN}$$

2.b) Moment Fléchissant Maximum à Mi-Portée

Les deux types de charge contribuent au moment fléchissant au centre de la poutre.

1. Moment dû à la UDL :

• Formule :

$$M_{\text{UDL}} = \frac{w\,L^2}{8}$$

• Calcul :

$$M_{\text{UDL}} = \frac{5\,\text{kN/m} \times (12\,\text{m})^2}{8}$$ $$M_{\text{UDL}} = \frac{5 \times 144}{8}$$ $$M_{\text{UDL}} = 90\,\text{kN}\cdot\text{m}$$

2. Moment dû à la Charge Concentrée :

• Formule :

$$M_{\text{point}} = \frac{P\,L}{4}$$

• Calcul :

$$M_{\text{point}} = \frac{10\,\text{kN} \times 12\,\text{m}}{4}$$ $$M_{\text{point}} = 30\,\text{kN}\cdot\text{m}$$

3. Moment Maximum Total :

$$M_{\text{max}} = M_{\text{UDL}} + M_{\text{point}}$$ $$M_{\text{max}} = 90\,\text{kN}\cdot\text{m} + 30\,\text{kN}\cdot\text{m}$$ $$M_{\text{max}} = 120\,\text{kN}\cdot\text{m}$$

2.c) Détermination de la Force de Traction dans la Zone Tendue

En flexion, la distribution de contrainte dans la section est linéaire. On calcule d’abord la contrainte de traction maximale, puis, en intégrant cette distribution sur la partie tendue de la section (la moitié inférieure), on peut déterminer la force résultante dans la zone en traction.

i) Calcul de l’Inertie de la Section et de la Distance Maximum

• Inertie (pour une section rectangulaire) :

$$I = \frac{b\,h^3}{12}$$

Calcul :

$$I = \frac{0,2 \times (0,3)^3}{12}$$ $$I = \frac{0,2 \times 0,027}{12}$$ $$I = \frac{0,0054}{12}$$ $$I \approx 0,00045\,\text{m}^4$$

• Distance maximale $c$ (du neutre à la fibre extrême) :

$$c = \frac{h}{2} = \frac{0,3}{2} = 0,15\,\text{m}$$

ii) Contrainte Maximale en Traction

• Formule (relation flexion) :

$$\sigma_{\text{max}} = \frac{M_{\text{max}}\,c}{I}$$

• Conversion :

$M_{\text{max}} = 120\,\text{kN}\cdot\text{m} = 120\,000\,\text{N}\cdot\text{m}$

• Calcul :

$$\sigma_{\text{max}} = \frac{120\,000\,\text{N}\cdot\text{m} \times 0,15\,\text{m}}{0,00045\,\text{m}^4}$$ $$\sigma_{\text{max}} = \frac{18\,000}{0,00045}$$ $$\sigma_{\text{max}} \approx 40\,000\,000\,\text{Pa}$$ $$\sigma_{\text{max}} = 40\,\text{MPa}$$

iii) Force Résultante dans la Zone en Traction

Pour une distribution linéaire de la contrainte (allant de 0 au neutre à $\sigma_{\text{max}}$ à la fibre extrême), la force résultante dans la zone tendue est obtenue par intégration.

• Méthode rapide :
  Pour une section rectangulaire, on montre que la force de traction $F_t$ dans la moitié tendue est donnée par :

$$F_t = \frac{3\,M_{\text{max}}}{2\,h}$$

• Calcul :

$$F_t = \frac{3 \times 120\,000\,\text{N}\cdot\text{m}}{2 \times 0,3\,\text{m}}$$ $$F_t = \frac{360\,000}{0,6}$$ $$F_t = 600\,000\,\text{N}$$ $$F_t = 600\,\text{kN}$$

Note : Cette force $600\,\text{kN}$ correspond à la somme (par intégration) des forces de traction réparties dans la zone tendue de la section. Elle n’est pas directement comparable aux réactions aux appuis (35 kN chacune) car elle résulte de l’intégration de la distribution de la contrainte due au moment fléchissant.

3. Vérification de la Contrainte de Traction Maximale

On compare la contrainte maximale calculée à la limite élastique du matériau.

• Contrainte maximale :

$$\sigma_{\text{max}} \approx 40\,\text{MPa}$$

• Limite élastique de l’acier :

$$\sigma_{\text{yield}} = 250\,\text{MPa}$$

• Comparaison :

$$40\,\text{MPa} < 250\,\text{MPa}$$

Conclusion : La contrainte en traction reste bien en deçà de la limite élastique. La poutre est donc adéquatement dimensionnée pour supporter les charges considérées.

Évaluation de la Capacité de Traction d’une Poutre

D’autres exercices de Rdm :

• Calcul de la position de l’axe neutre
• Calcul des déformations dans une poutre
• Charges, contraintes et déformations