Détermination du Module d’Young
Comprendre la Détermination du Module d’Young
Vous êtes ingénieur dans une entreprise de construction et vous devez vérifier la rigidité d’une poutre en acier avant de l’intégrer dans la structure d’un bâtiment. Pour cela, vous décidez de calculer le module d’Young de l’acier à partir d’un essai de traction.
Pour comprendre l’Évaluation de la Capacité de Traction d’une Poutre, cliquez sur le lien.
Données fournies:
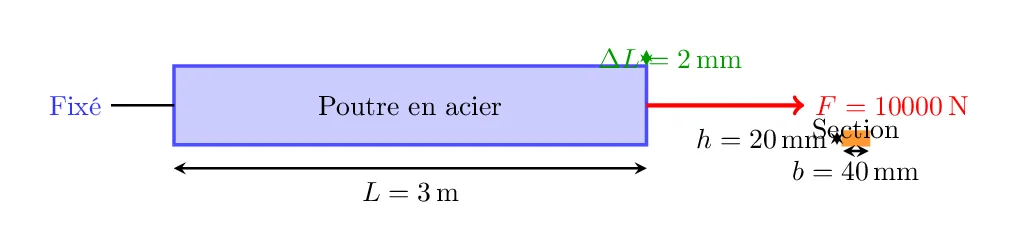
- Longueur initiale de la poutre en acier, L = 3 m
- Section transversale rectangulaire avec une largeur b = 40 mm et une hauteur h = 20 mm
- Force de traction appliquée, F = 10000 N
- Allongement mesuré de la poutre suite à l’application de la force, \(\Delta L = 2\) mm
Questions:
1. Calcul de l’aire de la section transversale (A)
2. Calcul de la contrainte (\(\sigma\)) dans la poutre
3. Calcul de la déformation unitaire (\(\epsilon\))
4. Calcul du module d’Young (E) de l’acier
5. Comparaison avec les valeurs typiques pour l’acier
- Les valeurs typiques du module d’Young pour l’acier varient entre 200 et 210 GPa. Comparez votre résultat à cette plage pour vérifier sa cohérence.
Correction : Détermination du Module d’Young
1. Calcul de l’aire de la section transversale (A)
La section de la poutre est rectangulaire. Pour calculer son aire, on utilise la formule :
\[ A = b \times h \]
Données :
- Largeur \( b = 40 \, \text{mm} \)
- Hauteur \( h = 20 \, \text{mm} \)
Attention aux unités :
On convertit les millimètres en mètres :
\[ b = 40 \, \text{mm} = 0,04 \, \text{m} \quad \text{et} \quad h = 20 \, \text{mm} = 0,02 \, \text{m} \]
Calcul :
\[ A = 0,04 \, \text{m} \times 0,02 \, \text{m} \] \[ A = 0,0008 \, \text{m}^2 \]
2. Calcul de la contrainte (\(\sigma\)) dans la poutre
La contrainte (ou stress) est définie comme la force appliquée par unité d’aire de la section transversale.
La formule est :
\[ \sigma = \frac{F}{A} \]
Données :
- Force \( F = 10\,000 \, \text{N} \)
- Aire \( A = 0,0008 \, \text{m}^2 \)
Calcul :
\[ \sigma = \frac{10\,000 \, \text{N}}{0,0008 \, \text{m}^2} \] \[ \sigma = 12\,500\,000 \, \text{Pa} \quad \text{(ou } 12,5 \, \text{MPa)} \]
3. Calcul de la déformation unitaire (\(\epsilon\))
La déformation unitaire (strain) se calcule en divisant l’allongement de la poutre par sa longueur initiale.
La formule est :
\[ \epsilon = \frac{\Delta L}{L} \]
Données :
- Allongement \( \Delta L = 2 \, \text{mm} \)
- Longueur initiale \( L = 3 \, \text{m} \)
Conversion :
\[ \Delta L = 2 \, \text{mm} = 0,002 \, \text{m} \]
Calcul :
\[ \epsilon = \frac{0,002 \, \text{m}}{3 \, \text{m}} \] \[ \epsilon \approx 0,0006667 \quad \text{(sans unité)} \]
4. Calcul du module d’Young (\(E\)) de l’acier
Le module d’Young est le rapport entre la contrainte appliquée et la déformation unitaire.
La formule est :
\[ E = \frac{\sigma}{\epsilon} \]
Données :
- \( \sigma = 12\,500\,000 \, \text{Pa} \)
- \( \epsilon \approx 0,0006667 \)
Calcul :
\[ E = \frac{12\,500\,000 \, \text{Pa}}{0,0006667} \] \[ E \approx 18\,750\,000\,000 \, \text{Pa} \]
On exprime le résultat en GPa (1 GPa = \( 10^9 \) Pa) :
\[ E \approx 18,75 \, \text{GPa} \]
5. Comparaison avec les valeurs typiques pour l’acier
Les valeurs usuelles du module d’Young pour l’acier se situent généralement entre 200 et 210 GPa.
Comparaison :
Notre résultat de \( E \approx 18,75 \, \text{GPa} \) est nettement inférieur à cette plage.
Conclusion :
La valeur obtenue indique une rigidité beaucoup plus faible que celle attendue pour l’acier. Cette divergence suggère :
- Soit une erreur expérimentale (par exemple, une mesure d’allongement trop importante ou une mauvaise estimation de la section),
- Soit que les données fournies ne correspondent pas à un acier classique.
Il conviendrait de vérifier les mesures et la méthode expérimentale pour identifier l’origine de cette incohérence.
Détermination du Module d’Young
D’autres exercices de Rdm:















Bonjour
Merci pour ce site et pour votre travail
Je comprends votre calcul de la déformation unitaire.
Par contre, lors du calcul de la contrainte, vous divisez des MPa par ce nombre sans dimension pour obtenir des Pa (première incompréhension pour moi). Ensuite, vous convertissez ces Pa en GPa (mais je compte un rapport de 1E6 et non de 1E5).
Pourriez-vous m’indiquer où je me trompe?
Merci d’avance
Frédéric
Bonjour Frédéric,
Merci pour votre commentaire. Vous avez raison, il y avait une erreur dans la conversion des unités pour le calcul du module d’Young. Après correction, le module d’Young est bien de 18.75 GPa, ce qui est effectivement beaucoup plus bas que la plage typique pour l’acier (200-210 GPa). Cette différence pourrait être due à des hypothèses de données ou des erreurs de mesure. Merci beaucoup de votre vigilance !