Contraintes et déformations en traction

Comprendre le Calcul des contraintes et déformations en traction

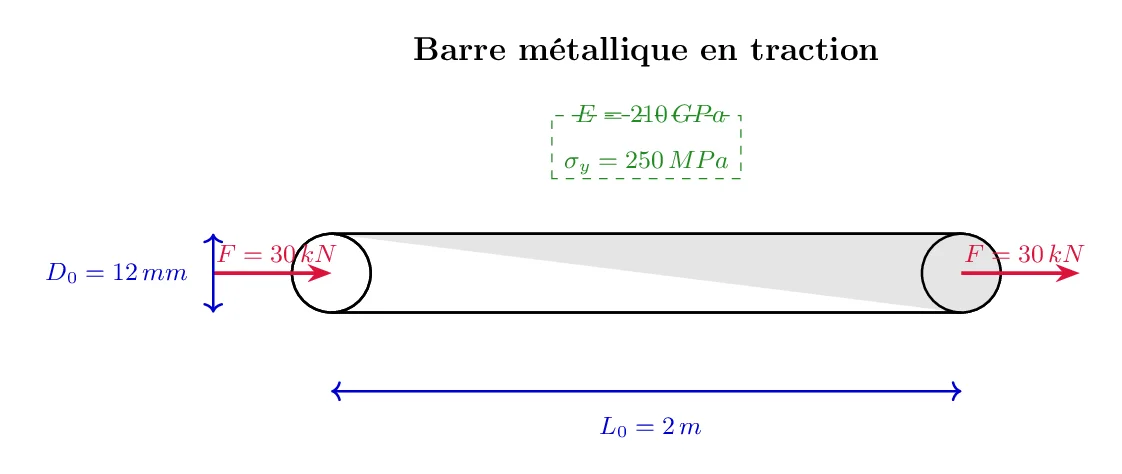
Une barre métallique cylindrique est soumise à une force de traction. Les caractéristiques de la barre et les forces appliquées sont les suivantes :

Diamètre initial de la barre (D₀) = 12 mm
Longueur initiale de la barre (L₀) = 2 m
Module d’élasticité du matériau (E) = 210 GPa
Limite d’élasticité du matériau (σy) = 250 MPa
Charge appliquée (F) = 30 kN

Pour comprendre le calcul de Traction et compression exercice corrigé, cliquez sur le lien.

Questions :

1. Calcul de la contrainte initiale : Calculez la contrainte initiale (σ) dans la barre.

2. Détermination de la déformation : Déterminez si la barre se déforme de manière élastique ou plastique.

3. Calcul de la déformation élastique : Si la déformation est élastique, calculez l’allongement (ΔL) de la barre.

4. Calcul de la nouvelle longueur : En supposant que la déformation est élastique, calculez la nouvelle longueur de la barre.

5. Discussion sur la déformation plastique : Si la contrainte dépasse la limite d’élasticité, discutez brièvement des conséquences potentielles sur la barre en termes de déformation plastique.

Correction : Contraintes et déformations en traction

1. Calcul de la contrainte initiale (\(\sigma\))

La contrainte (\(\sigma\)) dans une barre est définie par la formule :

\[ \sigma = \frac{F}{A} \]

où :

\(F\) est la force appliquée,
\(A\) est l’aire de la section transversale.

Pour une barre de section circulaire, l’aire se calcule par :

\[ A = \pi \left(\frac{D_0}{2}\right)^2 \]

Données

Force appliquée : \( F = 30 \,\text{kN} = 30\,000 \,\text{N} \)
Diamètre initial : \( D_0 = 12 \,\text{mm} = 0,012 \,\text{m} \)

Calcul

1. Calcul de l’aire de la section \( A \) :

\[ A = \pi \left(\frac{0,012}{2}\right)^2 = \pi \times (0,006)^2 \]

\[ (0,006)^2 = 0,000036 \,\text{m}^2 \] \[ \quad \Longrightarrow \quad A = \pi \times 0,000036 \approx 0,0001131 \,\text{m}^2 \]

2. Calcul de la contrainte \( \sigma \) :

\[ \sigma = \frac{F}{A} \] \[ \sigma = \frac{30\,000 \,\text{N}}{0,0001131 \,\text{m}^2} \] \[ \sigma \approx 265\,000\,000 \,\text{Pa} = 265 \,\text{MPa} \]

2. Détermination de la déformation : élastique ou plastique ?

Pour déterminer le type de déformation, on compare la contrainte calculée (\( \sigma \)) à la limite d’élasticité (\( \sigma_y \)) du matériau.

Si \( \sigma < \sigma_y \), la déformation est élastique (réversible).
Si \( \sigma \geq \sigma_y \), la déformation est plastique (déformation permanente).

Données

Contrainte calculée : \( \sigma \approx 265 \,\text{MPa} \)
Limite d’élasticité : \( \sigma_y = 250 \,\text{MPa} \)

Conclusion

Puisque \( 265 \,\text{MPa} > 250 \,\text{MPa} \), la contrainte appliquée dépasse la limite d’élasticité. La barre se déforme donc de manière plastique.
Remarque : La loi de Hooke, qui s’applique uniquement pour la déformation élastique, n’est pas totalement valide dans ce cas.

3. Calcul de la déformation élastique (hypothétique)

Note :

Bien que la barre subisse une déformation plastique, nous pouvons calculer l’allongement théorique si la déformation avait été purement élastique, afin de comprendre l’ordre de grandeur de l’allongement.

Formule

La loi de Hooke pour un matériau en traction donne :

\[ \Delta L = \frac{F \cdot L_0}{A \cdot E} \]

Données

Force appliquée : \( F = 30\,000 \,\text{N} \)
Longueur initiale : \( L_0 = 2 \,\text{m} \)
Aire de la section : \( A = 0,0001131 \,\text{m}^2 \)
Module d’élasticité : \( E = 210 \,\text{GPa} = 210 \times 10^9 \,\text{Pa} \)

Calcul

1. Calcul du numérateur :

\[ F \cdot L_0 = 30\,000 \,\text{N} \times 2 \,\text{m} \] \[ = 60\,000 \,\text{N·m}
\]

2. Calcul du dénominateur :

\[ A \cdot E = 0,0001131 \,\text{m}^2 \times 210 \times 10^9 \,\text{Pa} \]

D’abord, calculons \( 0,0001131 \times 210 \times 10^9 \) :

\[ 0,0001131 \times 210 \times 10^9 \approx 23\,751\,000 \,\text{N} \]

3. Calcul de \( \Delta L \) :

\[ \Delta L = \frac{60\,000}{23\,751\,000} \] \[ \Delta L \approx 0,002526 \,\text{m} \quad \text{soit environ } 2,53 \,\text{mm} \]

4. Calcul de la nouvelle longueur (hypothétique, si déformation purement élastique)

Formule

La nouvelle longueur \( L_{\text{nouvelle}} \) s’obtient par :

\[ L_{\text{nouvelle}} = L_0 + \Delta L \]

Calcul

\[ L_{\text{nouvelle}} = 2 \,\text{m} + 0,00253 \,\text{m} \] \[ L_{\text{nouvelle}} \approx 2,00253 \,\text{m} \]

Remarque :

Cette longueur serait obtenue si la déformation était purement élastique. Toutefois, ici la contrainte appliquée excède la limite d’élasticité, ce qui entraîne une déformation plastique.

5. Discussion sur la déformation plastique

Déformation plastique :
Quand la contrainte dépasse la limite d’élasticité (\( \sigma > \sigma_y \)), le matériau entre dans une phase de déformation plastique. Dans cette phase, le comportement n’est plus linéaire, et le matériau subit un allongement permanent même après le retrait de la charge.
Conséquences potentielles :
- Allongement permanent : La barre ne retrouvera pas sa longueur initiale après la suppression de la charge.
- Modification des propriétés mécaniques : La résistance et la ductilité du matériau peuvent être altérées, et le risque de rupture augmente si la charge continue à s’accroître.
- Diminution de la sécurité : Dans des applications structurelles, dépasser la limite d’élasticité peut compromettre l’intégrité et la durabilité de l’élément.

Conclusion sur le cas étudié

Dans notre exercice, la contrainte calculée est de \( 265 \,\text{MPa} \), ce qui est supérieur à la limite d’élasticité de \( 250 \,\text{MPa} \). Cela signifie que la barre se déforme de manière plastique et que l’allongement calculé par la loi de Hooke (2,53 mm) ne reflète pas le comportement réel du matériau sous cette charge. Le matériau subira une déformation permanente et la relation linéaire entre contrainte et déformation ne sera plus valable.

Contraintes et déformations en traction

D’autres exercices de Rdm :