Comportement plastique et la rupture

Comprendre le comportement plastique et la rupture

Un ingénieur conçoit une poutre en acier pour supporter une charge dans une construction industrielle. L’acier a un comportement élastoplastique et l’ingénieur doit s’assurer que la poutre ne subira ni déformation plastique excessive ni rupture sous la charge maximale prévue.

Pour comprendre la Théorie de la plasticité, cliquez sur le lien.

Données

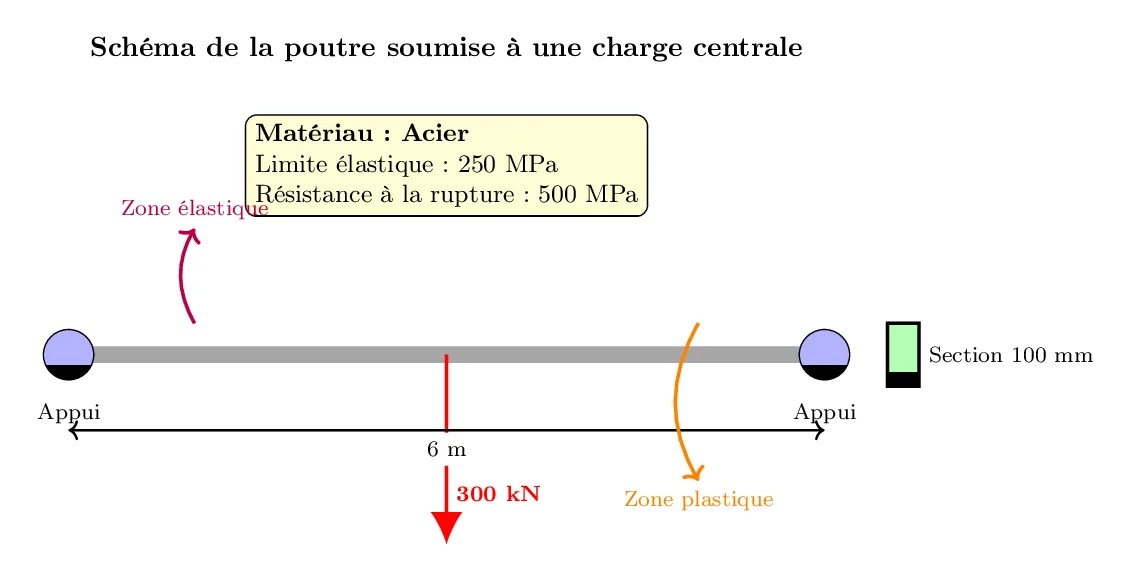
Matériau de la poutre: Acier, avec une limite élastique de 250 MPa et une résistance à la rupture de 500 MPa.
Dimensions de la poutre: Longueur = 6 m, section transversale carrée de côté 100 mm.
Charge maximale prévue: 300 kN appliquée au centre de la poutre.

Questions:

1. Calculer la contrainte dans la poutre sous la charge maximale.

2. Déterminer si la poutre subira une déformation plastique sous cette charge.

3. Calculer la charge maximale que la poutre peut supporter avant de subir une rupture.

Correction : comportement plastique et la rupture

1. Calcul de la contrainte (contrainte de flexion) sous la charge maximale

Étape 1 : Calcul du moment fléchissant maximum

Pour une poutre simplement appuyée avec une charge concentrée au centre, le moment fléchissant maximum est donné par :

\[ M_{max} = \frac{P \cdot L}{4} \]

Données :

\( P = 300\,000 \) N,
\( L = 6000 \) mm

Calcul :

\[ M_{max} = \frac{300\,000 \, \text{N} \times 6000 \, \text{mm}}{4} \] \[ M_{max} = \frac{1\,800\,000\,000 \, \text{N·mm}}{4} \] \[ M_{max} = 450\,000\,000 \, \text{N·mm} \]

Étape 2 : Calcul du moment d’inertie de la section

Pour une section carrée de côté \( a \), le moment d’inertie par rapport à l’axe neutre est :

\[ I = \frac{a^4}{12} \]

Données :

\( a = 100 \) mm

Calcul :

\[ I = \frac{100^4}{12} \] \[ I = \frac{100\,000\,000}{12} \] \[ I \approx 8\,333\,333 \, \text{mm}^4 \]

Étape 3 : Détermination de la distance \( c \) du centre de gravité à la fibre extrême

Pour une section carrée :

\[ c = \frac{a}{2} = \frac{100}{2} = 50 \, \text{mm} \]

Étape 4 : Calcul de la contrainte maximale en flexion

La contrainte de flexion est donnée par :

\[ \sigma = \frac{M_{max} \cdot c}{I} \]

Données :

\( M_{max} = 450\,000\,000 \, \text{N·mm} \)
\( c = 50 \) mm
\( I \approx 8\,333\,333 \, \text{mm}^4 \)

Calcul :

\[ \sigma = \frac{450\,000\,000 \times 50}{8\,333\,333} \] \[ \sigma \approx \frac{22\,500\,000\,000}{8\,333\,333} \] \[ \sigma \approx 2700 \, \text{MPa} \]

Résultat : La contrainte maximale en flexion sous la charge de 300 kN est d’environ 2700 MPa.

2. Détermination de la déformation plastique

La limite élastique de l’acier est de \( 250 \) MPa.
Nous avons obtenu une contrainte de 2700 MPa, ce qui est largement supérieur à \( 250 \) MPa.

Conclusion :
La poutre dépassera la limite d’élasticité et subira donc une déformation plastique dès l’application de la charge maximale de 300 kN. En réalité, la contrainte calculée excède même la résistance à la rupture (\( 500 \) MPa), indiquant une rupture imminente.

3. Calcul de la charge maximale admissible avant rupture

Pour éviter la rupture, la contrainte maximale ne doit pas dépasser la résistance à la rupture \( \sigma_{ult} = 500 \) MPa.
En reprenant la formule de la contrainte en flexion et en résolvant pour la charge \( P \) :

\[ \sigma_{ult} = \frac{M_{max} \cdot c}{I} \quad \text{avec} \quad M_{max} = \frac{P_{max} \cdot L}{4} \]

On a donc :

\[ \sigma_{ult} = \frac{P_{max} \cdot L \cdot c}{4I} \]

Isolons \( P_{max} \) :

\[ P_{max} = \frac{4\,I\,\sigma_{ult}}{L\,c} \]

Données :

\( I \approx 8\,333\,333 \, \text{mm}^4 \)
\( \sigma_{ult} = 500 \) MPa \( = 500 \, \text{N/mm}^2 \)
\( L = 6000 \) mm
\( c = 50 \) mm

Calcul :

\[ P_{max} = \frac{4 \times 8\,333\,333 \times 500}{6000 \times 50} \] \[ P_{max} = \frac{16\,666\,666\,500}{300\,000} \] \[ P_{max} \approx 55\,555.56 \, \text{N} \] \[ P_{max} \approx 55.6 \, \text{kN} \]

Résultat : La charge maximale admissible avant que la contrainte n’atteigne la résistance à la rupture est d’environ 55.6 kN.

Conclusion Générale

1. Contrainte en flexion sous 300 kN : \(\sigma \approx 2700 \, \text{MPa}\)

2. Comportement plastique : La contrainte dépasse largement la limite d’élasticité de 250 MPa, donc la poutre subira une déformation plastique (et même une rupture, puisque \(2700 \, \text{MPa} > 500 \, \text{MPa}\)).

3. Charge maximale admissible avant rupture : \(P_{max} \approx 55.6 \, \text{kN}\)

Ce calcul montre que, avec les dimensions et les propriétés mécaniques données, la poutre est gravement surchargée sous une charge de 300 kN. Pour une conception sécurisée, soit les dimensions de la poutre doivent être augmentées, soit le matériau doit être repensé pour supporter la charge sans atteindre le comportement plastique ni la rupture.

Comportement plastique et la rupture

D’autres exercices de Rdm :

Comportement plastique et la rupture