Études de cas pratique

EGC

Choix de Profilés Métalliques

Choix de Profilés Métalliques pour une Poutre en Acier

Choix de Profilés Métalliques pour une Poutre en Acier

Comprendre le Choix de Profilés Métalliques

Le choix d'un profilé métallique approprié est une étape clé dans la conception d'une charpente. Il s'agit de sélectionner une section d'acier (par exemple, un IPE, HEA, UPN, etc.) dont les caractéristiques géométriques et mécaniques permettent de résister aux sollicitations de calcul tout en optimisant le poids et le coût. Pour une poutre soumise à la flexion, l'un des critères principaux est que son moment résistant de calcul (\(M_{Rd}\)) soit supérieur ou égal au moment fléchissant de calcul agissant (\(M_{Ed}\)). Cela implique souvent de déterminer un module de section plastique requis (\(W_{pl,y,req}\)) et de choisir un profilé dans un catalogue qui satisfait cette exigence.

Données de l'étude

On doit choisir un profilé IPE en acier S275 pour une poutre simplement appuyée, soumise à un moment fléchissant à l'ELU.

Caractéristiques et Sollicitations :

  • Moment fléchissant de calcul à l'ELU (\(M_{Ed}\)) : \(120 \, \text{kN} \cdot \text{m}\)
  • Nuance d'acier : S275 (\(f_y = 275 \, \text{MPa}\))
  • Coefficient partiel de sécurité pour la résistance des sections (\(\gamma_{M0}\)) : \(1.0\)

Extrait de catalogue de profilés IPE (valeurs indicatives) :

Profilé \(W_{pl,y} (\text{cm}^3)\) Poids (kg/m)
IPE 200 221 22.4
IPE 220 285 26.2
IPE 240 367 30.7
IPE 270 484 36.1
IPE 300 628 42.2
IPE 330 797 49.1
IPE 360 1019 57.1

Hypothèse : On considère des sections de classe 1 ou 2, permettant d'utiliser le module de section plastique. Le déversement est supposé empêché.

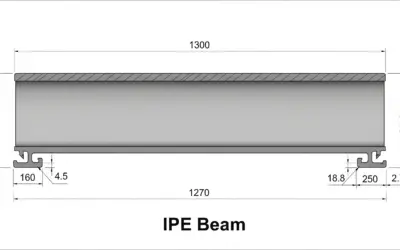
Schéma : Poutre en Acier et Section IPE
Poutre en flexion M_Ed Portée L Section IPE b h

Poutre en acier soumise à un moment fléchissant et section transversale type IPE.

Questions à traiter

  1. Calculer la résistance de calcul de l'acier (\(f_{yd}\)).
  2. Déterminer le module de section plastique minimal requis (\(W_{pl,y,req}\)) pour la poutre.
  3. En utilisant l'extrait de catalogue fourni, choisir le profilé IPE le plus léger qui satisfait la condition \(W_{pl,y} \geq W_{pl,y,req}\).
  4. Calculer le moment résistant plastique (\(M_{pl,Rd}\)) du profilé IPE choisi.
  5. Vérifier si le profilé choisi est adéquat en comparant \(M_{Ed}\) à \(M_{pl,Rd}\).

Correction : Choix de Profilés Métalliques pour une Poutre en Acier

Question 1 : Résistance de Calcul de l'Acier (\(f_{yd}\))

Principe :

La résistance de calcul de l'acier (\(f_{yd}\)) est la limite d'élasticité caractéristique (\(f_y\)) divisée par le coefficient partiel de sécurité pour la résistance des sections (\(\gamma_{M0}\)). C'est la contrainte maximale que l'acier peut atteindre en service à l'ELU avant de plastifier de manière significative.

Formule(s) utilisée(s) :
\[f_{yd} = \frac{f_y}{\gamma_{M0}}\]
Données spécifiques :
  • Limite d'élasticité de l'acier S275 (\(f_y\)) : \(275 \, \text{MPa}\)
  • Coefficient partiel de sécurité (\(\gamma_{M0}\)) : \(1.0\)
Calcul :
\[ \begin{aligned} f_{yd} &= \frac{275 \, \text{MPa}}{1.0} \\ &= 275 \, \text{MPa} \, (\text{ou N/mm}^2) \end{aligned} \]
Résultat Question 1 : La résistance de calcul de l'acier est \(f_{yd} = 275 \, \text{MPa}\).

Question 2 : Module de Section Plastique Requis (\(W_{pl,y,req}\))

Principe :

Pour qu'une section résiste à un moment fléchissant \(M_{Ed}\) en utilisant sa pleine capacité plastique (sections de classe 1 ou 2), son moment résistant plastique \(M_{pl,Rd} = W_{pl,y} \cdot f_{yd}\) doit être au moins égal à \(M_{Ed}\). On peut donc déterminer le module de section plastique minimal requis \(W_{pl,y,req}\) en réarrangeant cette relation.

Formule(s) utilisée(s) :
\[W_{pl,y,req} = \frac{M_{Ed}}{f_{yd}}\]

(En supposant \(\gamma_{M0}=1.0\) implicitement dans \(f_{yd}\) ou en l'incluant : \(W_{pl,y,req} = \frac{M_{Ed} \cdot \gamma_{M0}}{f_y}\))

Données spécifiques (convertir les unités pour la cohérence) :
  • \(M_{Ed} = 120 \, \text{kN} \cdot \text{m} = 120 \times 10^6 \, \text{N} \cdot \text{mm}\)
  • \(f_{yd} = 275 \, \text{N/mm}^2\) (calculée)
Calcul :
\[ \begin{aligned} W_{pl,y,req} &= \frac{120 \times 10^6 \, \text{N} \cdot \text{mm}}{275 \, \text{N/mm}^2} \\ &\approx 436363.64 \, \text{mm}^3 \end{aligned} \]

Conversion en cm³ (puisque le catalogue est en cm³) : \(1 \, \text{cm}^3 = 1000 \, \text{mm}^3\).

\[ W_{pl,y,req} \approx \frac{436363.64}{1000} \, \text{cm}^3 \approx 436.36 \, \text{cm}^3 \]
Résultat Question 2 : Le module de section plastique requis est \(W_{pl,y,req} \approx 436.36 \, \text{cm}^3\).

Quiz Intermédiaire 1 : Si la limite d'élasticité de l'acier (\(f_y\)) était plus élevée, le \(W_{pl,y,req}\) pour le même \(M_{Ed}\) serait :

Question 3 : Choix du Profilé IPE

Principe :

On consulte un catalogue de profilés pour trouver le profilé IPE le plus léger (donc généralement le plus économique) dont le module de section plastique (\(W_{pl,y}\)) est supérieur ou égal au module requis (\(W_{pl,y,req}\)).

Données spécifiques :
  • \(W_{pl,y,req} \approx 436.36 \, \text{cm}^3\)
  • Extrait du catalogue :
    Profilé\(W_{pl,y} (\text{cm}^3)\)Poids (kg/m)
    IPE 200 221 22.4
    IPE 220 285 26.2
    IPE 240 367 30.7
    IPE 270 484 36.1
    IPE 300 628 42.2
Choix :

En comparant \(W_{pl,y,req} \approx 436.36 \, \text{cm}^3\) aux valeurs du catalogue :

  • IPE 240 : \(W_{pl,y} = 367 \, \text{cm}^3 < 436.36 \, \text{cm}^3\) (Insuffisant)
  • IPE 270 : \(W_{pl,y} = 484 \, \text{cm}^3 \geq 436.36 \, \text{cm}^3\) (Suffisant)
  • IPE 300 : \(W_{pl,y} = 628 \, \text{cm}^3 \geq 436.36 \, \text{cm}^3\) (Suffisant, mais plus lourd que IPE 270)

Le profilé IPE 270 est le plus léger qui satisfait la condition.

Résultat Question 3 : Le profilé IPE 270 est choisi, avec \(W_{pl,y} = 484 \, \text{cm}^3\).

Question 4 : Moment Résistant Plastique (\(M_{pl,Rd}\)) du Profilé Choisi

Principe :

Le moment résistant plastique du profilé choisi (IPE 270) est calculé en utilisant son module de section plastique réel (\(W_{pl,y,choisi}\)) et la résistance de calcul de l'acier (\(f_{yd}\)).

Formule(s) utilisée(s) :
\[M_{pl,Rd} = \frac{W_{pl,y,choisi} \cdot f_y}{\gamma_{M0}}\]
Données spécifiques :
  • Profilé choisi : IPE 270, avec \(W_{pl,y,choisi} = 484 \, \text{cm}^3 = 484 \times 10^3 \, \text{mm}^3\)
  • \(f_y = 275 \, \text{MPa} = 275 \, \text{N/mm}^2\)
  • \(\gamma_{M0} = 1.0\)
Calcul :
\[ \begin{aligned} M_{pl,Rd} &= \frac{(484 \times 10^3 \, \text{mm}^3) \times (275 \, \text{N/mm}^2)}{1.0} \\ &= 133100000 \, \text{N} \cdot \text{mm} \end{aligned} \]

Conversion en kN·m :

\[ M_{pl,Rd} = \frac{133100000}{10^6} \, \text{kN} \cdot \text{m} = 133.1 \, \text{kN} \cdot \text{m} \]
Résultat Question 4 : Le moment résistant plastique du profilé IPE 270 choisi est \(M_{pl,Rd} = 133.1 \, \text{kN} \cdot \text{m}\).

Question 5 : Vérification Finale du Profilé Choisi

Principe :

On vérifie si le moment résistant plastique du profilé choisi (\(M_{pl,Rd}\)) est bien supérieur ou égal au moment fléchissant de calcul agissant (\(M_{Ed}\)).

Formule(s) utilisée(s) :
\[M_{Ed} \leq M_{pl,Rd}\]
Données spécifiques :
  • \(M_{Ed} = 120 \, \text{kN} \cdot \text{m}\)
  • \(M_{pl,Rd} = 133.1 \, \text{kN} \cdot \text{m}\) (pour IPE 270)
Comparaison :
\[120 \, \text{kN} \cdot \text{m} \leq 133.1 \, \text{kN} \cdot \text{m} \quad (\text{OK})\]

La condition est vérifiée. Le profilé IPE 270 est adéquat pour reprendre le moment fléchissant de calcul.

Résultat Question 5 : Le profilé IPE 270 choisi est adéquat car son moment résistant (\(133.1 \, \text{kN} \cdot \text{m}\)) est supérieur au moment sollicitant (\(120 \, \text{kN} \cdot \text{m}\)).

Quiz Intermédiaire 2 : Si, après calcul, on trouve que \(M_{Ed} > M_{pl,Rd}\) pour le profilé choisi, que doit-on faire ?

Quiz Rapide : Testez vos connaissances

1. Qu'est-ce qu'un profilé IPE en charpente métallique ?

2. L'acier S275 a une limite d'élasticité caractéristique (\(f_y\)) de :

3. Le module de section plastique (\(W_{pl,y}\)) est utilisé pour calculer le moment résistant :

Glossaire

Charpente Métallique
Structure porteuse constituée d'éléments en acier assemblés (poutres, poteaux, contreventements).
Profilé IPE
Profilé en I à ailes parallèles (Européen), standardisé, utilisé couramment pour les poutres.
Acier S275
Nuance d'acier de construction structural ayant une limite d'élasticité minimale garantie de \(275 \, \text{MPa}\).
Limite d'Élasticité (\(f_y\))
Contrainte à partir de laquelle un matériau commence à se déformer plastiquement (déformation permanente).
État Limite Ultime (ELU)
État limite correspondant à la capacité portante maximale de la structure ou d'un de ses éléments avant rupture ou perte de stabilité.
Moment Fléchissant de Calcul (\(M_{Ed}\))
Moment sollicitant la section, calculé à l'ELU à partir des charges pondérées.
Module de Section Plastique (\(W_{pl,y}\))
Caractéristique géométrique d'une section qui, multipliée par la limite d'élasticité, donne le moment de plastification complète de la section.
Moment Résistant Plastique (\(M_{pl,Rd}\) ou \(M_{c,Rd}\))
Capacité maximale en flexion d'une section capable de plastification, calculée à l'ELU.
Coefficient Partiel de Sécurité (\(\gamma_{M0}\))
Coefficient appliqué à la résistance du matériau pour obtenir la résistance de calcul pour la vérification de la résistance des sections.
Choix de Profilés Métalliques – Exercice d'Application

D’autres exercices de structure métallique:

0 commentaires
Soumettre un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *