Capacité Portante d’une Semelle Isolée
Comprendre la Capacité Portante d’une Semelle Isolée
Dans le cadre de la conception d’une structure résidentielle, il est nécessaire de déterminer la capacité portante d’une semelle isolée qui supportera un pilier de charge. Cette semelle est essentielle pour assurer la stabilité et la sécurité de la structure. L’objectif est de calculer la capacité portante de la semelle en considérant les contraintes du sol et les charges appliquées.
Pour comprendre le Calcul des Dimensions de la Semelle, cliquez sur le lien.
Données fournies:
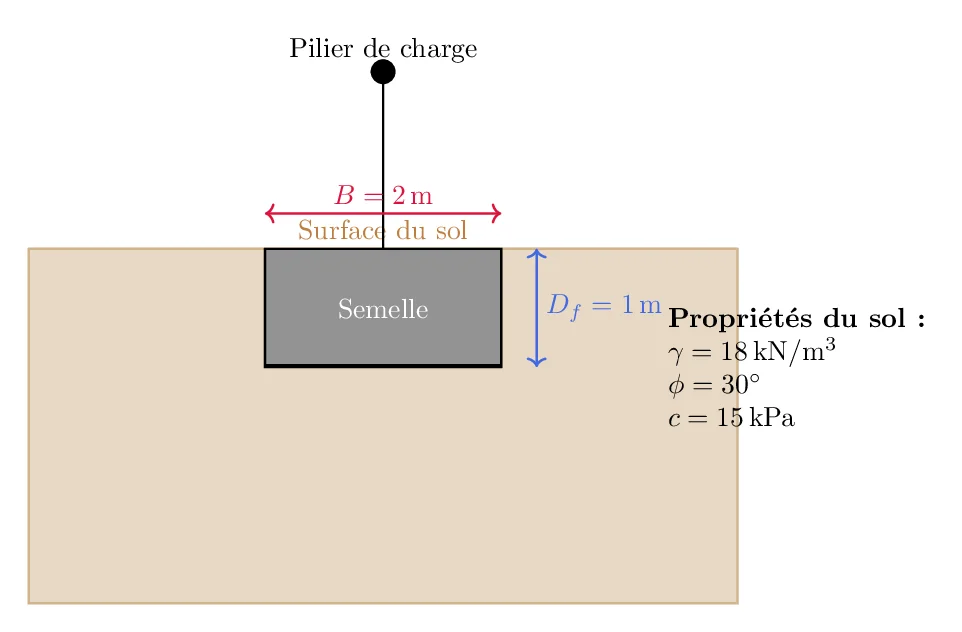
Dimensions de la semelle:
- Largeur \(B = 2\,m\)
- Longueur \(L = 2\,m\)
- Profondeur d’encastrement \(D_f = 1\,m\)
Propriétés du sol:
- Poids volumique du sol, \(\gamma = 18\, \text{kN/m}^3\)
- Angle de frottement interne, \(\phi = 30^\circ\)
- Cohésion, \(c = 15\, \text{kPa}\)
Charge appliquée sur la semelle: \(P = 450\, \text{kN}\)
Questions:
1. Calculer la capacité portante ultime \(q_u\) de la semelle en utilisant la formule de Terzaghi pour les fondations superficielles.
2. Déterminer la capacité portante nette \(q_n\).
3. Calculer la pression de service admissible \(q_a\) en considérant un facteur de sécurité \(FS = 3\).
4. Vérifier si la charge appliquée \(P\) est supportable par la semelle, en comparant \(q_a\) avec la pression due à \(P\) sur la base de la semelle.
Correction : Capacité Portante d’une Semelle Isolée
1. Calcul de la capacité portante ultime \( q_u \)
Formule de Terzaghi
Pour une semelle superficielle, la formule de Terzaghi s’exprime classiquement sous la forme :
\[ q_u = c \, N_c + \gamma \, D_f \, N_q + \frac{1}{2} \, \gamma \, B \, N_\gamma \]
- \( c \) : cohésion du sol
- \( \gamma \) : poids volumique du sol
- \( D_f \) : profondeur d’encastrement
- \( B \) : largeur de la semelle (pour une semelle carrée, \( B = L \))
- \( N_c, \, N_q, \, N_\gamma \) : facteurs de capacité portante qui dépendent de l’angle de frottement interne \( \phi \)
Données fournies
- \(c = 15 \, \text{kPa}\)
- \(\gamma = 18 \, \text{kN/m}^3\)
- \(D_f = 1 \, \text{m}\)
- \(B = 2 \, \text{m} \quad (\text{et } L = 2 \, \text{m})\)
- \(\phi = 30^\circ\)
Calcul des facteurs de capacité portante
En utilisant la méthode de Terzaghi et les relations usuelles pour \( \phi = 30^\circ \), on obtient approximativement :
- \( N_q \):
\[ N_q = e^{\pi \tan \phi} \times \tan^2\left(45^\circ+\frac{\phi}{2}\right) \]
Pour \( \phi = 30^\circ \) :
\(\tan 30^\circ \approx 0.577\)
\(\tan\left(45^\circ+15^\circ\right) = \tan 60^\circ \approx 1.732\)
Ainsi, \(\tan^2 60^\circ \approx 3\) et \( e^{\pi \times 0.577} \approx e^{1.81} \approx 6.11 \)
Donc,
\[ N_q \approx 6.11 \times 3 \approx 18.33 \]
- \( N_c \):
\[ N_c = \frac{N_q – 1}{\tan \phi} \] \[ N_c \approx \frac{18.33 – 1}{0.577} \] \[ N_c \approx \frac{17.33}{0.577} \approx 30.0 \]
- \( N_\gamma \):
\[ N_\gamma = 2 (N_q + 1) \, \tan \phi \] \[ N_\gamma \approx 2 \times (18.33+1) \times 0.577 \] \[ N_\gamma \approx 2 \times 19.33 \times 0.577 \] \[ N_\gamma \approx 22.33 \]
Substitution des valeurs
1. Premier terme :
\[ c \, N_c = 15 \, \text{kPa} \times 30.0 = 450 \, \text{kPa} \]
2. Deuxième terme :
\[ \gamma \, D_f \, N_q = 18 \, \text{kN/m}^3 \times 1 \, \text{m} \times 18.33 \] \[ \approx 329.94 \, \text{kPa} \]
3. Troisième terme :
\[ \frac{1}{2} \, \gamma \, B \, N_\gamma = \frac{1}{2} \times 18 \, \text{kN/m}^3 \times 2 \, \text{m} \times 22.33 \]
- Calcul intermédiaire : \(\frac{1}{2} \times 18 \times 2 = 18 \, \text{kN/m}^2\)
- Puis :
\[ 18 \times 22.33 \approx 401.94 \, \text{kPa} \]
Somme totale :
\[ q_u = 450 + 329.94 + 401.94 \] \[ q_u \approx 1181.88 \, \text{kPa} \]
Capacité portante ultime : \( q_u \approx 1182 \, \text{kPa} \)
2. Calcul de la capacité portante nette \( q_n \)
La capacité portante nette se calcule en soustrayant la pression exercée par le sol au niveau de la semelle (pression de survenance \( q_0 \)) de \( q_u \).
Calcul de \( q_0 \)
\[ q_0 = \gamma \, D_f \] \[ q_0 = 18 \, \text{kN/m}^3 \times 1 \, \text{m} \] \[ q_0 = 18 \, \text{kPa} \]
Substitution
\[ q_n = q_u – q_0 \] \[ q_n = 1181.88 \, \text{kPa} – 18 \, \text{kPa} \] \[ q_n \approx 1163.88 \, \text{kPa} \]
Capacité portante nette : \( q_n \approx 1164 \, \text{kPa} \)
3. Calcul de la pression de service admissible \( q_a \)
Pour obtenir la pression de service admissible, on divise la capacité portante nette par le facteur de sécurité (FS).
Donnée :
- \(FS = 3\)
Formule
\[ q_a = \frac{q_n}{FS} \]
Substitution
\[ q_a = \frac{1163.88 \, \text{kPa}}{3} \approx 387.96 \, \text{kPa} \]
Pression de service admissible : \(q_a \approx 388 \, \text{kPa}\)
4. Vérification de la portance par rapport à la charge appliquée
Données :
- \(P = 450 \, \text{kN}\)
- \(A = B \times L = 2 \, \text{m} \times 2 \, \text{m} = 4 \, \text{m}^2\)
Calcul de la pression due à \( P \) sur la base
\[ q_{\text{appliquée}} = \frac{P}{A} = \frac{450 \, \text{kN}}{4 \, \text{m}^2} \] \[ q_{\text{appliquée}} = 112.5 \, \text{kN/m}^2 = 112.5 \, \text{kPa} \]
Comparaison
- \(q_a \approx 388 \, \text{kPa}\)
- \(q_{\text{appliquée}} = 112.5 \, \text{kPa}\)
Conclusion :
Puisque \( q_a > q_{\text{appliquée}} \), la semelle est capable de supporter la charge appliquée.
Capacité Portante d’une Semelle Isolée
D’autres exercices de fondation:






0 commentaires