Calculs de Résistance et Déformation des Éléments Métalliques
Comprendre les Calculs de Résistance et Déformation
Vous êtes ingénieur(e) en construction métallique et travaillez sur la conception d’un hangar industriel. Le hangar aura une charpente principalement composée de poutres et de colonnes en acier. Pour assurer la sécurité et la durabilité de la structure, vous devez calculer la résistance et la déformation des éléments clés de la charpente sous les charges prévues, notamment le poids de la toiture, l’effet du vent, et les charges utiles.
Pour comprendre le Calcul des charges de vent sur une structure et le Calcul de la charge de neige sur une toiture, cliquez sur les liens.
Données:
- Matériau: Acier S355
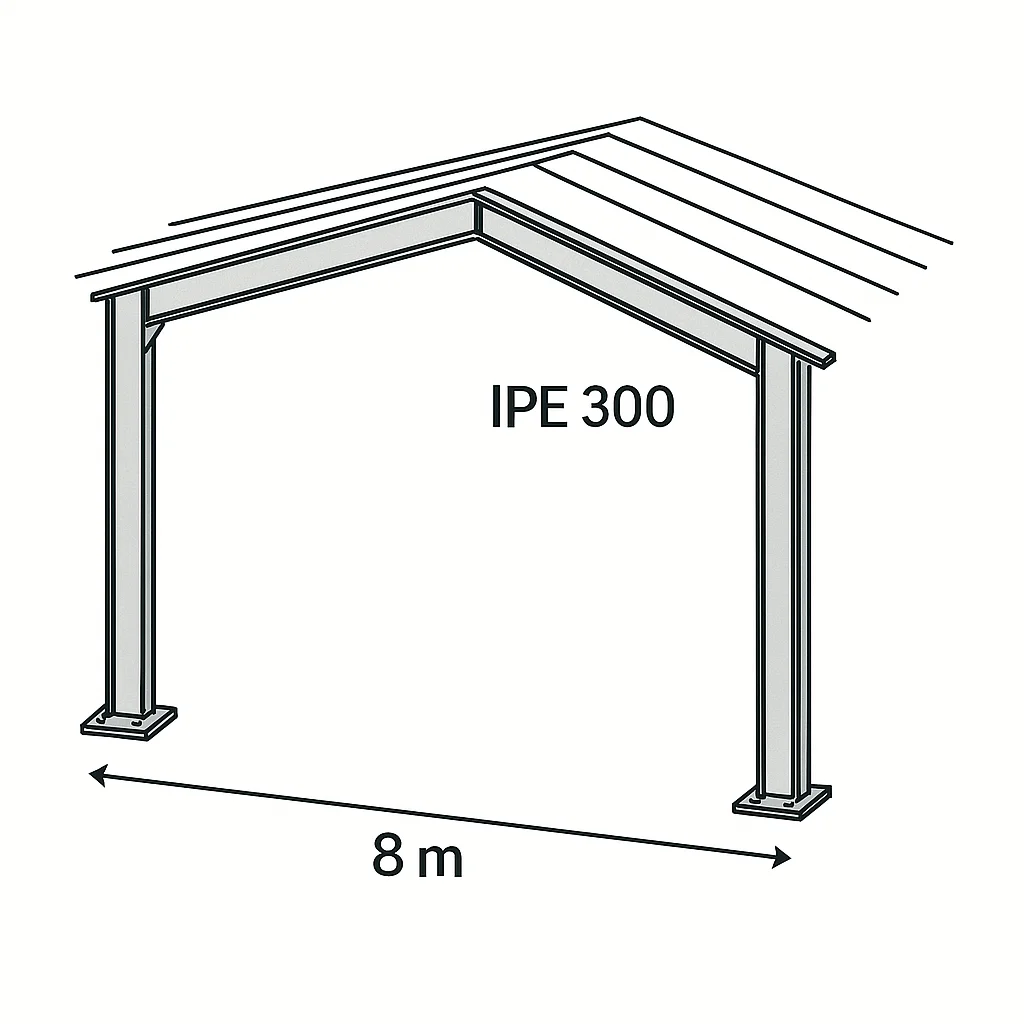
- Profil de la poutre: IPE 300
- Longueur de la poutre: 8 mètres
- Charge permanente (G, incluant le poids propre de la poutre): 5 kN/m
- Charge d’exploitation (Q, charge utile): 3 kN/m
- Charge de vent (W): 1.5 kN/m sur la face latérale
- Module d’élasticité de l’acier (E): 210 GPa
- Moment d’inertie de la section (I): \(7900\, \text{cm}^4\)
Questions:
1. Calcul de la charge totale appliquée à la poutre
- Calculer la charge totale linéaire qui agit sur la poutre en tenant compte de la charge permanente, de la charge d’exploitation, et de l’effet du vent.
2. Calcul du moment fléchissant maximal (Mmax)
- En utilisant la théorie des poutres sur deux appuis simples et en considérant la charge totale calculée précédemment, déterminer le moment fléchissant maximal dans la poutre. Utiliser l’hypothèse que la charge est uniformément répartie sur toute la longueur de la poutre.
3. Calcul de la contrainte maximale dans la poutre
- En utilisant le moment fléchissant maximal obtenu, calculer la contrainte maximale dans la poutre
4. Calcul de la flèche maximale de la poutre
- Calculer la flèche maximale (déformation verticale) au milieu de la poutre due à la charge totale.
Correction : Calculs de Résistance et Déformation
1. Calcul de la charge totale appliquée à la poutre
Étape 1.1 : Rassembler les données
-
Charge permanente (G) : 5 kN/m
-
Charge d’exploitation (Q) : 3 kN/m
-
Charge de vent (W) : 1,5 kN/m
Étape 1.2 : Formule et Calcul
La charge totale linéaire \( w_{\text{total}} \) est la somme des trois charges :
\[ w_{\text{total}} = G + Q + W \]
Substitution des valeurs :
\[ w_{\text{total}} = 5 \; \text{kN/m} + 3 \; \text{kN/m} + 1,5 \; \text{kN/m} \] \[ w_{\text{total}} = 9,5 \; \text{kN/m} \]
2. Calcul du moment fléchissant maximal (\(M_{\text{max}}\))
Étape 2.1 : Rassembler les données
- Longueur de la poutre (L) : 8 m
- Charge totale linéaire (\(w_{\text{total}}\)) : 9,5 kN/m
Étape 2.2 : Formule
Pour une poutre simplement appuyée soumise à une charge uniformément répartie, le moment fléchissant maximal se calcule par :
\[ M_{\text{max}} = \frac{w_{\text{total}} \times L^2}{8} \]
Étape 2.3 : Calcul
Substitution des valeurs :
\[ M_{\text{max}} = \frac{9,5 \; \text{kN/m} \times (8 \; \text{m})^2}{8} \] \[ M_{\text{max}} = \frac{9,5 \times 64}{8} \; \text{kN·m} \] \[ M_{\text{max}} = \frac{608}{8} \; \text{kN·m} \] \[ M_{\text{max}} = 76 \; \text{kN·m} \]
Remarque : Pour les calculs ultérieurs, on peut convertir en N·m :
\(76 \; \text{kN·m} = 76 \times 10^3 \; \text{N·m}\).
3. Calcul de la contrainte maximale dans la poutre
Étape 3.1 : Rassembler les données
– Moment fléchissant maximal (\(M_{\text{max}}\))} : 76 kN·m = \(76 \times 10^3 \; \text{N·m}\)
– Section de la poutre : Profil IPE 300
- La hauteur totale \(h = 300 \; \text{mm}\)
- On prend \(y = \frac{h}{2} = 150 \; \text{mm} = 0,15 \; \text{m}\)
– Moment d’inertie (I) : 7900 cm\(^4\)
- Conversion en m\(^4\) :
\(1 \; \text{cm}^4 = 1 \times 10^{-8} \; \text{m}^4\)
\[ I = 7900 \times 10^{-8} \; \text{m}^4 \] \[ I = 7,9 \times 10^{-5} \; \text{m}^4 \]
Étape 3.2 : Formule
La contrainte de flexion maximale \( \sigma_{\text{max}} \) se calcule par :
\[ \sigma_{\text{max}} = \frac{M_{\text{max}} \times y}{I} \]
Étape 3.3 : Calcul
Substitution des valeurs :
\[ \sigma_{\text{max}} = \frac{76 \times 10^3 \; \text{N·m} \times 0,15 \; \text{m}}{7,9 \times 10^{-5} \; \text{m}^4} \] \[ \sigma_{\text{max}} = \frac{11\,400}{7,9 \times 10^{-5}} \; \text{Pa} \] \[ \sigma_{\text{max}} \approx 144\,300\,000 \; \text{Pa} \quad \text{soit environ } 144,3 \; \text{MPa} \]
4. Calcul de la flèche maximale de la poutre
Étape 4.1 : Rassembler les données
- Charge totale linéaire (\(w_{\text{total}}\)) : 9,5 kN/m = 9500 N/m
- Longueur de la poutre (L) : 8 m
- Module d’élasticité de l’acier (E)} : 210 GPa = \(210 \times 10^9 \; \text{N/m}^2\)
- Moment d’inertie (I) : \(7,9 \times 10^{-5} \; \text{m}^4\)
Étape 4.2 : Formule
Pour une poutre simplement appuyée sous charge uniformément répartie, la flèche maximale \(\delta_{\text{max}}\) est donnée par :
\[ \delta_{\text{max}} = \frac{5 \, w_{\text{total}} \, L^4}{384 \, E \, I} \]
Étape 4.3 : Calcul
Substitution des valeurs :
- \(w_{\text{total}} = 9500 \; \text{N/m}\)
- \(L^4 = 8^4 = 4096 \; \text{m}^4\)
On a donc :
\[ \delta_{\text{max}} = \frac{5 \times 9500 \times 4096}{384 \times 210 \times 10^9 \times 7,9 \times 10^{-5}} \] \[ \delta_{\text{max}} = \frac{194\,560\,000}{6\,370\,560\,000} \; \text{m} \] \[ \delta_{\text{max}} \approx 0,03053 \; \text{m} \]
En millimètres :
\[ 0,03053 \; \text{m} \times 1000 = 30,53 \; \text{mm} \]
Calculs de Résistance et Déformation
D’autres exercices de structure métallique:











0 commentaires