Calcul les gisements et coordonnées polaires

Comprendre le Calcul les gisements et coordonnées polaires

Vous êtes un topographe travaillant sur un nouveau projet de développement urbain. Votre tâche est de cartographier une zone spécifique pour planifier la construction de nouvelles infrastructures. Vous avez plusieurs points de repère et vous devez calculer les gisements et les coordonnées polaires entre ces points.

Pour comprendre le Calcul des coordonnées en topographie, cliquez sur le lien.

Données:

Points de Repère:

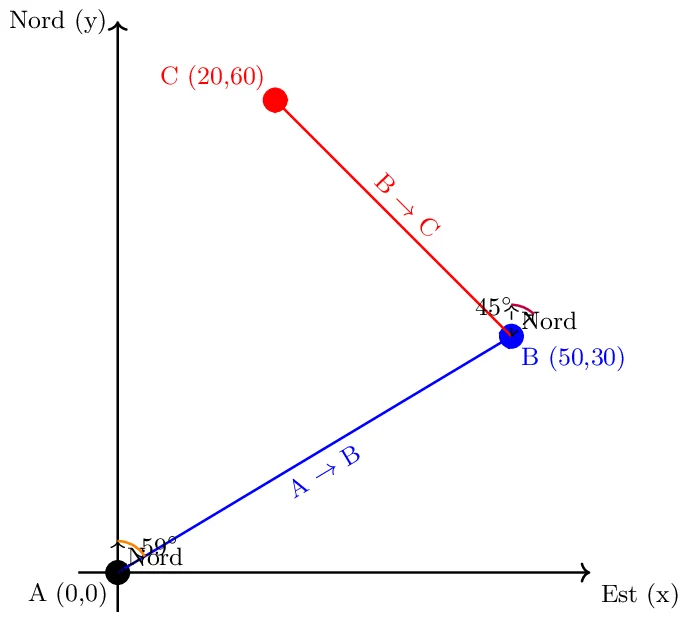
Point A: Coordonnées (x: 0, y: 0) – Point de départ.
Point B: Coordonnées (x: 50, y: 30).
Point C: Coordonnées (x: 20, y: 60).

Calcul les gisements et coordonnées polaires

Questions:

1. Calculer le gisement du point A vers le point B.

2. Calculer le gisement du point B vers le point C.

3. Déterminer les coordonnées polaires (distance et angle) du point A au point B, puis du point B au point C.

Correction : Calcul les gisements et coordonnées polaires

Données du problème

Point A : (0 ; 0) – Point de départ.
Point B : (50 ; 30)
Point C : (20 ; 60)

On rappelle que :

Le gisement (ou azimut) est l’angle mesuré dans le sens des aiguilles d’une montre à partir du Nord (direction positive de l’axe y) vers la ligne joignant deux points.
Les coordonnées polaires d’un point par rapport à un autre sont données par la distance entre les deux points et le gisement.

Formules utilisées:

1. Calcul du gisement:

Pour passer d’un point \(P_1(x_1,y_1)\) à un point \(P_2(x_2,y_2)\), on définit :

\(\Delta x = x_2 – x_1\)
\(\Delta y = y_2 – y_1\)

Le gisement \(G\) est alors calculé en tenant compte du quadrant dans lequel se situe le vecteur \((\Delta x, \Delta y)\) :

Si \(\Delta y > 0\) et \(\Delta x \ge 0\) (premier quadrant)} :

\[ G = \arctan\left(\frac{\Delta x}{\Delta y}\right) \]

Si \(\Delta y > 0\) et \(\Delta x < 0\) (deuxième quadrant par rapport au Nord) :

\[ G = 360^\circ – \arctan\left(\frac{|\Delta x|}{\Delta y}\right) \]

(D’autres cas s’appliquent pour \(\Delta y \le 0\), mais ici, les déplacements considérés se font avec \(\Delta y > 0\).)

2. Calcul de la distance:

La distance \(d\) entre deux points est donnée par la formule :

\[ d = \sqrt{(\Delta x)^2 + (\Delta y)^2} \]

1. Calcul du gisement du point A vers le point B

Étape 1 : Calcul des différences

\(\Delta x_{AB} = x_B – x_A = 50 – 0 = 50\)
\(\Delta y_{AB} = y_B – y_A = 30 – 0 = 30\)

Les deux différences sont positives, donc le vecteur se trouve dans le premier quadrant (déplacement nord-est).

Étape 2 : Application de la formule

Puisque \(\Delta y_{AB} > 0\) et \(\Delta x_{AB} \ge 0\) :

\[ G_{AB} = \arctan\left(\frac{\Delta x_{AB}}{\Delta y_{AB}}\right) = \arctan\left(\frac{50}{30}\right) \]

Étape 3 : Calcul numérique

\[ \frac{50}{30} \approx 1,6667 \] \[ \arctan(1,6667) \approx 59,04^\circ \]

Résultat :
Le gisement de A vers B est d’environ 59,04°.

2. Détermination des coordonnées polaires du point A vers le point B

Étape 1 : Calcul de la distance

\[ d_{AB} = \sqrt{(50)^2 + (30)^2} \] \[ d_{AB} = \sqrt{2500 + 900} \] \[ d_{AB} = \sqrt{3400} \approx 58,31 \text{ m} \]

Étape 2 : Angle (gisement)

Nous avons déjà trouvé que le gisement est environ 59,04°.

Résultat :
Les coordonnées polaires de B par rapport à A sont :

Distance : environ 58,31 m
Angle (gisement) : environ 59,04°

3. Calcul du gisement du point B vers le point C

Étape 1 : Calcul des différences

Pour le segment \(B \rightarrow C\) :

\(\Delta x_{BC} = x_C – x_B = 20 – 50 = -30\)
\(\Delta y_{BC} = y_C – y_B = 60 – 30 = 30\)

Ici, \(\Delta y_{BC} > 0\) et \(\Delta x_{BC} < 0\), le vecteur se situe donc dans la zone correspondant à une direction nord-ouest.

Étape 2 : Application de la formule

Pour un déplacement avec \(\Delta y > 0\) et \(\Delta x < 0\) :

\[ G_{BC} = 360^\circ – \arctan\left(\frac{|\Delta x_{BC}|}{\Delta y_{BC}}\right) \]

Calculons :

\[ \frac{|\Delta x_{BC}|}{\Delta y_{BC}} = \frac{30}{30} = 1 \] \[ \arctan(1) = 45^\circ \]

Donc :

\[ G_{BC} = 360^\circ – 45^\circ = 315^\circ \]

Résultat :
Le gisement de B vers C est de 315°.

4. Détermination des coordonnées polaires du point B vers le point C

Étape 1 : Calcul de la distance

\[ d_{BC} = \sqrt{(-30)^2 + (30)^2} \] \[ d_{BC} = \sqrt{900 + 900} \] \[ d_{BC} = \sqrt{1800} \approx 42,43 \text{ m} \]

Étape 2 : Angle (gisement)

Le gisement a été calculé précédemment comme 315°.

Résultat :
Les coordonnées polaires de C par rapport à B sont :

Distance : environ 42,43 m
Angle (gisement) : 315°

Conclusion

Du point A vers le point B :
- Gisement : environ 59,04°
- Distance : environ 58,31 m
Du point B vers le point C :
- Gisement : 315°
- Distance : environ 42,43 m