Calcul des Aciers d’un Poteau
Comprendre le Calcul des aciers d’un poteau
Vous êtes chargé de concevoir un poteau en béton armé pour un bâtiment de bureaux. Le poteau doit respecter les normes de l’Eurocode 2 (EN 1992-1-1) pour les structures en béton.
Pour comprendre le Calcul de la Section d’Armature d’une poutre, cliquez sur le lien.
Données :
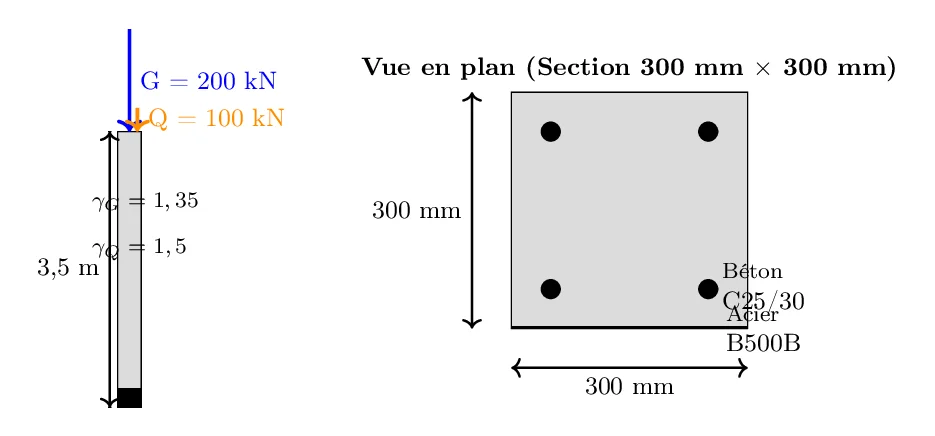
- Hauteur du poteau : 3,5 m
- Section transversale du poteau : carrée, 300 mm x 300 mm
- Béton : C25/30
- Acier : B500B
- Charges permanentes (G) : 200 kN
- Charges variables (Q) : 100 kN
- Coefficients de sécurité selon l’Eurocode : γ_G = 1,35, γ_Q = 1,5
Questions :
1. Détermination des Charges de Calcul : Calculez les charges de conception en utilisant les combinaisons de charges selon l’Eurocode.
2. Calcul de l’Effort Axial : Déterminez l’effort axial maximal que le poteau doit supporter.
3. Vérification de la Section de Béton : Vérifiez si la section en béton choisie est adéquate pour supporter les charges calculées, en tenant compte de la résistance du béton.
4. Calcul des Aciers Nécessaires :
- Déterminez la quantité d’acier nécessaire pour armer le poteau. Utilisez les formules de l’Eurocode pour le calcul des armatures en traction/compression.
- Vérifiez le pourcentage minimal et maximal d’armature requis selon l’Eurocode.
5. Disposition des Armatures : Proposez un arrangement d’armatures (nombre et disposition des barres) qui respecte les exigences de l’Eurocode en termes de recouvrement, d’espacement et de protection contre la corrosion.
6. Vérification de la Stabilité au Flambement : Assurez-vous que le poteau est stable contre le flambement en suivant les lignes directrices de l’Eurocode.
Correction : calcul des aciers d’un poteau :
1. Calcul des charges de calcul
Les charges de calcul (ou actions de conception) se déterminent en appliquant aux charges caractéristiques les coefficients partiels conformément à l’Eurocode 2.
Formule :
\[ N_{Ed} = \gamma_G\,G + \gamma_Q\,Q \]
Données :
- \( G = 200\;\mathrm{kN} \)
- \( Q = 100\;\mathrm{kN} \)
- \( \gamma_G = 1{,}35 \)
- \( \gamma_Q = 1{,}5 \)
Calcul :
\[ N_{Ed} = 1{,}35 \times 200\;\mathrm{kN} + 1{,}5 \times 100\;\mathrm{kN} \] \[ N_{Ed} = 270\;\mathrm{kN} + 150\;\mathrm{kN} \] \[ N_{Ed} = 420\;\mathrm{kN} \]
2. Calcul de l’effort axial
L’effort axial maximal que le poteau doit supporter est la charge de calcul obtenue précédemment.
\[ N_{Ed} = 420\;\mathrm{kN} \]
3. Vérification de la section de béton
Avant de dimensionner l’armature, il faut s’assurer que la section en béton choisie offre une résistance suffisante à la compression. La résistance de la section en béton (sans armatures) se calcule en multipliant l’aire brute par la résistance de calcul du béton.
Formule :
\[ N_{Rd,\,béton} = A_c \times f_{cd} \]
avec
\[ f_{cd} = \frac{f_{ck}}{\gamma_c} \]
Données :
- Section brute :
\[ A_c = b \times b \] \[ A_c = 300\;\mathrm{mm} \times 300\;\mathrm{mm} \] \[ A_c = 90\,000\;\mathrm{mm^2} \]
- \( f_{ck} = 25\;\mathrm{MPa} \)
- \( \gamma_c = 1{,}5 \) \(\Rightarrow f_{cd} = \frac{25}{1{,}5} \approx 16{,}67\;\mathrm{MPa}\)
Calcul :
\[ N_{Rd,\,béton} = 90\,000\;\mathrm{mm^2} \times 16{,}67\;\mathrm{N/mm^2} \] \[ N_{Rd,\,béton} \approx 1\,500\,300\;\mathrm{N} \approx 1500\;\mathrm{kN} \]
Conclusion :
La capacité en compression de la section en béton, \(1500\;\mathrm{kN}\), est largement supérieure à l’effort axial \(420\;\mathrm{kN}\). La section est donc adéquate du point de vue du béton.
4. Calcul des aciers nécessaires
La résistance ultime du poteau est assurée par la somme de la résistance du béton et de celle des armatures :
\[ N_{Rd} = A_c\,f_{cd} + A_s\,f_{yd} \]
Pour un poteau soumis uniquement à la compression, si \(N_{Ed}\) est très inférieur à \(A_c\,f_{cd}\), la contribution de l’acier par équilibre serait négative. Cependant, l’Eurocode impose un taux minimal d’armature pour assurer la ductilité et le contrôle des fissures.
Cas d’équilibre (hypothétique) :
\[ A_s = \frac{N_{Ed} – A_c\,f_{cd}}{f_{yd}} \]
Ici,
\[ A_c\,f_{cd} = 1500\;\mathrm{kN} \quad \text{et} \quad N_{Ed} = 420\;\mathrm{kN} \]
Ce qui donnerait une valeur négative, donc l’équilibre ne nécessite pas d’armature complémentaire.
Application du minimum requis :
L’Eurocode (et les pratiques courantes) impose un taux minimal d’armature. Pour un poteau, il est usuel de retenir environ 1% de l’aire brute.
Données :
\[ A_{s,\text{min}} = 0{,}01 \times A_c \] \[ A_{s,\text{min}} = 0{,}01 \times 90\,000\;\mathrm{mm^2} \] \[ A_{s,\text{min}} = 900\;\mathrm{mm^2} \]
Conclusion :
On retiendra une armature totale minimale de
\[ A_s = 900\;\mathrm{mm^2} \]
5. Disposition des armatures
L’agencement doit respecter les exigences de l’Eurocode en termes de recouvrement, d’espacement et de protection contre la corrosion. Pour un poteau de section carrée, la solution classique consiste à disposer des barres aux quatre angles.
Proposition d’armature :
- Option : Utiliser 4 barres de diamètre \( \phi = 18\;\mathrm{mm} \).
Calcul de l’aire d’une barre :
\[ A_{\text{barre}} = \frac{\pi}{4} \times \phi^2 \] \[ A_{\text{barre}} = \frac{\pi}{4} \times (18\;\mathrm{mm})^2 \] \[ A_{\text{barre}} \approx 254{,}47\;\mathrm{mm^2} \]
Aire totale :
\[ A_{s,\text{proposé}} = 4 \times 254{,}47\;\mathrm{mm^2} \] \[ A_{s,\text{proposé}} \approx 1018\;\mathrm{mm^2} \]
Vérification du taux d’armature :
\[ \text{Taux d’armature} = \frac{1018}{90\,000} \approx 1{,}13\% \]
Ce taux est supérieur au minimum de 1% et reste dans des limites raisonnables (les taux typiques se situant souvent entre 1% et 4% pour des poteaux en compression).
Remarque sur la disposition :
- Le recouvrement minimal (généralement 40 mm pour des éléments porteurs dans des bâtiments) doit être respecté.
- Les barres doivent être espacées de manière à assurer une bonne répartition de l’armature et à faciliter la coulée du béton.
6. Vérification de la stabilité au flambement
Même si la charge axiale est faible par rapport à la capacité de la section en béton, il est nécessaire de vérifier que le poteau n’est pas sujet au flambement (instabilité globale) compte tenu de son rapport d’élancement.
Étape 6.1 : Calcul du rapport d’élancement
Formule :
\[ \lambda = \frac{L_{eff}}{r} \]
où \( L_{eff} \) est la longueur efficace (dépendant des conditions d’appui) et \( r \) est le rayon de giration de la section.
- Calcul du rayon de giration pour une section carrée :
\[ r = \frac{b}{\sqrt{12}} \] \[ r = \frac{300\;\mathrm{mm}}{\sqrt{12}} \] \[ r \approx \frac{300}{3{,}464} \approx 86{,}6\;\mathrm{mm} \]
- Supposons pour une vérification conservatrice que la longueur efficace est égale à la hauteur réelle (appuis simples) :
\[ L_{eff} = 3500\;\mathrm{mm} \]
- Calcul du rapport d’élancement :
\[ \lambda = \frac{3500\;\mathrm{mm}}{86{,}6\;\mathrm{mm}} \approx 40{,}4 \]
Étape 6.2 : Vérification du flambement
- Pour une colonne en béton armé, la stabilité est vérifiée au moyen de méthodes prenant en compte le flambement élastique et les imperfections (interaction béton–acier).
- Dans notre cas, la charge de calcul \(420\;\mathrm{kN}\) est très faible par rapport à la capacité en compression de la section (\(1500\;\mathrm{kN}\)) et même en tenant compte d’une réduction de capacité due à un élancement modéré, le risque de flambement reste faible.
- Remarque : En pratique, si la colonne est soumise à un rapport d’élancement d’environ 40, une étude plus détaillée (analyse non linéaire ou utilisation de courbes d’instabilité selon l’Eurocode) pourrait être réalisée. Cependant, compte tenu de la faible intensité de la charge axiale, la stabilité globale est assurée.
Conclusion :
Le poteau, avec un rapport d’élancement approximatif de 40, est jugé stable pour l’effort axial considéré.
Conclusion finale :
Le poteau en béton armé, avec une section carrée de \(300\;\mathrm{mm} \times 300\;\mathrm{mm}\) et soumis à une charge de calcul de \(420\;\mathrm{kN}\), est vérifié du point de vue de la capacité du béton et de la stabilité. L’armature minimale imposée par l’Eurocode (1% de la section, soit \(900\;\mathrm{mm^2}\)) est respectée. Une solution pratique consiste à utiliser 4 barres de diamètre 18 mm, offrant une aire totale d’environ \(1018\;\mathrm{mm^2}\), avec une disposition adéquate assurant recouvrement, espacement et protection contre la corrosion.
Calcul des aciers d’un poteau
D’autres exercices de béton armé :















0 commentaires