Calcul l'effort tranchant et le moment

Comprendre le Calcul de l’Effort Tranchant et du Moment Fléchissant

L'analyse de l'effort tranchant et du moment fléchissant est une étape fondamentale dans la conception et la vérification des structures porteuses, telles que les poutres. Lorsqu'une poutre est soumise à des charges (réparties ou concentrées), des efforts internes se développent en chaque section de la poutre pour maintenir l'équilibre. L'effort tranchant ($V$) représente la somme algébrique des forces verticales agissant à gauche (ou à droite) d'une section. Le moment fléchissant ($M$) représente la somme algébrique des moments des forces par rapport à cette section. La connaissance de la variation de ces efforts le long de la poutre, généralement représentée par des diagrammes, permet de déterminer les contraintes maximales et de s'assurer que la poutre peut résister aux charges appliquées sans rupture ni déformation excessive.

Données de l'étude

Vous êtes ingénieur en structure et vous devez analyser une poutre simplement appuyée. Cette poutre supporte plusieurs charges réparties et concentrées.

Caractéristiques de la poutre et des charges :

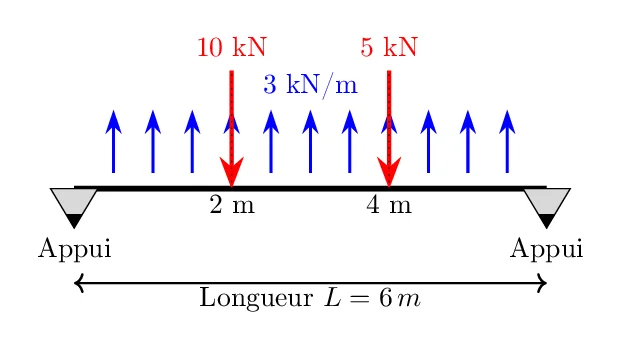
Longueur de la poutre, $L$: $6 \, \text{m}$
Une charge uniformément répartie ($w$) de $3 \, \text{kN/m}$ sur toute la longueur de la poutre.
Une charge ponctuelle ($P_1$) de $10 \, \text{kN}$ appliquée à $x_1 = 2 \, \text{m}$ du support gauche.
Une charge ponctuelle ($P_2$) de $5 \, \text{kN}$ appliquée à $x_2 = 4 \, \text{m}$ du support gauche.
La poutre est simplement appuyée à ses deux extrémités (appui simple à gauche, A, et appui à rouleau à droite, B).

Schéma : Poutre Simplement Appuyée avec Charges

Schéma de la poutre avec les charges et les appuis.

Questions à traiter

Réactions aux Appuis : Calculez les réactions aux appuis de la poutre ($R_A$ et $R_B$).
Effort Tranchant $V(x)$ :
1. Établissez les équations de l'effort tranchant $V(x)$ pour les différentes sections de la poutre.
2. Tracez le diagramme de l’effort tranchant (DET) pour la poutre.
3. Calculez l’effort tranchant à $x=1 \, \text{m}$, $x=3 \, \text{m}$ et $x=5 \, \text{m}$ de l’extrémité gauche.
Moment Fléchissant $M(x)$ :
1. Établissez les équations du moment fléchissant $M(x)$ pour les différentes sections de la poutre.
2. Tracez le diagramme du moment fléchissant (DMF) pour la poutre.
3. Calculez le moment fléchissant à $x=1 \, \text{m}$, $x=3 \, \text{m}$ et $x=5 \, \text{m}$ de l’extrémité gauche.
Point de Moment Maximal : Déterminez la position et la valeur du moment fléchissant maximal ($M_{\text{max}}$) dans la poutre.

Correction : Calcul de l’Effort Tranchant et du Moment Fléchissant

Question 1 : Réactions aux Appuis ($R_A$ et $R_B$)

Principe :

Pour une poutre en équilibre statique, la somme des forces verticales doit être nulle ($\sum F_y = 0$) et la somme des moments par rapport à n'importe quel point doit être nulle ($\sum M = 0$). On utilise ces deux conditions d'équilibre pour déterminer les réactions inconnues aux appuis $R_A$ et $R_B$.

Convention de signe adoptée : Forces vers le haut positives, moments dans le sens anti-horaire positifs.

Formule(s) utilisée(s) :

\sum F_y = 0 \] \[ \sum M_A = 0

Données spécifiques :

Charge répartie $w = 3 \, \text{kN/m}$ sur une longueur $L = 6 \, \text{m}$. La force résultante de cette charge répartie est $W = w \times L = 3 \, \text{kN/m} \times 6 \, \text{m} = 18 \, \text{kN}$, appliquée au milieu de la charge, soit à $L/2 = 3 \, \text{m}$ de l'appui A.
Charge ponctuelle $P_1 = 10 \, \text{kN}$ à $x_1 = 2 \, \text{m}$ de A.
Charge ponctuelle $P_2 = 5 \, \text{kN}$ à $x_2 = 4 \, \text{m}$ de A.

Calcul :

Pour trouver $R_B$, on applique la condition de somme des moments par rapport à l'appui A nulle ($\sum M_A = 0$) :

\begin{aligned} \sum M_A &= 0 \\ R_B \cdot L - P_1 \cdot x_1 - P_2 \cdot x_2 - W \cdot \frac{L}{2} &= 0 \\ R_B \cdot (6 \, \text{m}) - (10 \, \text{kN} \cdot 2 \, \text{m}) - (5 \, \text{kN} \cdot 4 \, \text{m}) - (18 \, \text{kN} \cdot 3 \, \text{m}) &= 0 \\ 6 R_B - 20 \, \text{kN}\cdot\text{m} - 20 \, \text{kN}\cdot\text{m} - 54 \, \text{kN}\cdot\text{m} &= 0 \\ 6 R_B - 94 \, \text{kN}\cdot\text{m} &= 0 \\ 6 R_B &= 94 \, \text{kN}\cdot\text{m} \\ R_B &= \frac{94}{6} \, \text{kN} = \frac{47}{3} \, \text{kN} \\ R_B &\approx 15.67 \, \text{kN} \end{aligned}

Pour trouver $R_A$, on applique la condition de somme des forces verticales nulle ($\sum F_y = 0$) :

\begin{aligned} \sum F_y &= 0 \\ R_A + R_B - P_1 - P_2 - W &= 0 \\ R_A + \frac{47}{3} \, \text{kN} - 10 \, \text{kN} - 5 \, \text{kN} - 18 \, \text{kN} &= 0 \\ R_A + \frac{47}{3} \, \text{kN} - 33 \, \text{kN} &= 0 \\ R_A &= 33 \, \text{kN} - \frac{47}{3} \, \text{kN} \\ R_A &= \frac{99}{3} \, \text{kN} - \frac{47}{3} \, \text{kN} \\ R_A &= \frac{52}{3} \, \text{kN} \\ R_A &\approx 17.33 \, \text{kN} \end{aligned}

Vérification : Somme des charges descendantes = $10 \, \text{kN} + 5 \, \text{kN} + 18 \, \text{kN} = 33 \, \text{kN}$. Somme des réactions ascendantes = $R_A + R_B = \frac{52}{3} \, \text{kN} + \frac{47}{3} \, \text{kN} = \frac{99}{3} \, \text{kN} = 33 \, \text{kN}$. L'équilibre des forces verticales est bien vérifié.

Résultat Question 1 :

Réaction à l'appui A : $R_A = \frac{52}{3} \, \text{kN} \approx 17.33 \, \text{kN}$
Réaction à l'appui B : $R_B = \frac{47}{3} \, \text{kN} \approx 15.67 \, \text{kN}$

Question 2 : Effort Tranchant $V(x)$

Principe :

L'effort tranchant $V(x)$ en une section $x$ (mesurée depuis l'appui gauche A) est la somme algébrique des forces verticales agissant à gauche de cette section. Une force vers le haut est comptée positivement, une force vers le bas négativement. La charge répartie $w$ contribue par une force $-wx$ à une distance $x$.

a. Équations de l'effort tranchant :

On définit les sections en fonction des points d'application des charges ponctuelles.

Section 1 : $0 \le x < 2 \, \text{m}$ (avant la charge $P_1$) $V(x) = R_A - w x = \frac{52}{3} - 3x$
Section 2 : $2 \le x < 4 \, \text{m}$ (après $P_1$ et avant $P_2$) $V(x) = R_A - w x - P_1 = \frac{52}{3} - 3x - 10 = \frac{22}{3} - 3x$
Section 3 : $4 \le x \le 6 \, \text{m}$ (après $P_2$) $V(x) = R_A - w x - P_1 - P_2 = \frac{52}{3} - 3x - 10 - 5 = \frac{7}{3} - 3x$

b. Tracé du diagramme de l’effort tranchant (DET) :

Le diagramme est tracé en calculant les valeurs de $V(x)$ aux extrémités de chaque section et juste avant/après les charges ponctuelles pour montrer les discontinuités.

À $x=0^+$ (juste à droite de l'appui A) : $V(0^+) = R_A = \frac{52}{3} \approx 17.33 \, \text{kN}$
À $x=2^-$ (juste avant $P_1$) : $V(2^-) = \frac{52}{3} - 3(2) = \frac{52-18}{3} = \frac{34}{3} \approx 11.33 \, \text{kN}$
À $x=2^+$ (juste après $P_1$) : $V(2^+) = V(2^-) - P_1 = \frac{34}{3} - 10 = \frac{34-30}{3} = \frac{4}{3} \approx 1.33 \, \text{kN}$
À $x=4^-$ (juste avant $P_2$) : $V(4^-) = \frac{22}{3} - 3(4) = \frac{22-36}{3} = -\frac{14}{3} \approx -4.67 \, \text{kN}$
À $x=4^+$ (juste après $P_2$) : $V(4^+) = V(4^-) - P_2 = -\frac{14}{3} - 5 = \frac{-14-15}{3} = -\frac{29}{3} \approx -9.67 \, \text{kN}$
À $x=6^-$ (juste avant l'appui B) : $V(6^-) = \frac{7}{3} - 3(6) = \frac{7-54}{3} = -\frac{47}{3} \approx -15.67 \, \text{kN}$. On note que $V(6^-) = -R_B$, ce qui est une vérification.

Diagramme de l'Effort Tranchant (DET)

Le diagramme montre une décroissance linéaire dans chaque segment, avec des sauts vers le bas aux points d'application de $P_1$ et $P_2$.

c. Calcul de l’effort tranchant à des points spécifiques :

\begin{aligned} V(1 \, \text{m}) &= \frac{52}{3} - 3(1) = \frac{52-9}{3} = \frac{43}{3} \, \text{kN} \approx 14.33 \, \text{kN} \\ V(3 \, \text{m}) &= \frac{22}{3} - 3(3) = \frac{22-27}{3} = -\frac{5}{3} \, \text{kN} \approx -1.67 \, \text{kN} \\ V(5 \, \text{m}) &= \frac{7}{3} - 3(5) = \frac{7-45}{3} = -\frac{38}{3} \, \text{kN} \approx -12.67 \, \text{kN} \end{aligned}

Résultat Question 2 :

Équations de V(x) établies pour chaque section.
Diagramme tracé.
$V(1 \, \text{m}) \approx 14.33 \, \text{kN}$
$V(3 \, \text{m}) \approx -1.67 \, \text{kN}$
$V(5 \, \text{m}) \approx -12.67 \, \text{kN}$

Quiz Intermédiaire 2 : L'effort tranchant dans une poutre est maximal (en valeur absolue) :

Toujours au milieu de la poutre.
Généralement près des appuis ou aux points d'application de charges concentrées importantes.
Là où le moment fléchissant est nul.
Toujours nul sous une charge répartie.

Question 3 : Moment Fléchissant $M(x)$

Principe :

Le moment fléchissant $M(x)$ en une section $x$ est la somme algébrique des moments des forces (réactions et charges) agissant à gauche de cette section, par rapport à la section. Il est aussi l'intégrale de l'effort tranchant : $M(x) = \int V(x) dx$. Un moment qui tend à courber la poutre avec une concavité vers le haut (sourire) est généralement considéré comme positif.

a. Équations du moment fléchissant :

Section 1 : $0 \le x < 2 \, \text{m}$ $M(x) = R_A x - \frac{wx^2}{2} = \frac{52}{3}x - \frac{3}{2}x^2$
Section 2 : $2 \le x < 4 \, \text{m}$ $M(x) = R_A x - \frac{wx^2}{2} - P_1(x-2) = \frac{52}{3}x - \frac{3}{2}x^2 - 10(x-2)$
Section 3 : $4 \le x \le 6 \, \text{m}$ $M(x) = R_A x - \frac{wx^2}{2} - P_1(x-2) - P_2(x-4) = \frac{52}{3}x - \frac{3}{2}x^2 - 10(x-2) - 5(x-4)$
Alternativement, pour la section 3, en partant de l'appui B (avec $x'$ mesuré depuis B, donc $x' = L-x = 6-x$) :
$M(x) = R_B (6-x) - \frac{w(6-x)^2}{2} = \frac{47}{3}(6-x) - \frac{3}{2}(6-x)^2$

b. Tracé du diagramme du moment fléchissant (DMF) :

Le diagramme est tracé en calculant les valeurs de $M(x)$ aux points clés et aux points où l'effort tranchant est nul.

$M(0) = 0$
$M(1) = \frac{52}{3}(1) - \frac{3}{2}(1)^2 = \frac{95}{6} \approx 15.83 \, \text{kN}\cdot\text{m}$
$M(2) = \frac{52}{3}(2) - \frac{3(2)^2}{2} = \frac{104}{3} - 6 = \frac{86}{3} \approx 28.67 \, \text{kN}\cdot\text{m}$
À $x = \frac{22}{9} \approx 2.44 \, \text{m}$ (où $V(x)=0$) : $M(\frac{22}{9}) = \frac{52}{3}(\frac{22}{9}) - \frac{3}{2}(\frac{22}{9})^2 - 10(\frac{22}{9}-2) = \frac{782}{27} \approx 28.96 \, \text{kN}\cdot\text{m}$ (Moment maximal)
$M(3) = \frac{52}{3}(3) - \frac{3(3)^2}{2} - 10(3-2) = 52 - 13.5 - 10 = 28.5 \, \text{kN}\cdot\text{m}$
$M(4) = \frac{52}{3}(4) - \frac{3(4)^2}{2} - 10(4-2) - 5(4-4) = \frac{208}{3} - 24 - 20 = \frac{76}{3} \approx 25.33 \, \text{kN}\cdot\text{m}$
$M(5) = \frac{47}{3}(6-5) - \frac{3}{2}(6-5)^2 = \frac{47}{3} - \frac{3}{2} = \frac{85}{6} \approx 14.17 \, \text{kN}\cdot\text{m}$
$M(6) = 0$

Diagramme du Moment Fléchissant (DMF)

Le diagramme est constitué de segments de paraboles (du second degré) avec des changements de pente aux points d'application des charges $P_1$ et $P_2$.

c. Calcul du moment fléchissant à des points spécifiques :

\begin{aligned} M(1 \, \text{m}) &= \frac{52}{3}(1) - \frac{3}{2}(1)^2 = \frac{52}{3} - \frac{3}{2} = \frac{104-9}{6} = \frac{95}{6} \, \text{kN}\cdot\text{m} \approx 15.83 \, \text{kN}\cdot\text{m} \\ M(3 \, \text{m}) &= \frac{52}{3}(3) - \frac{3}{2}(3)^2 - 10(3-2) = 52 - \frac{27}{2} - 10 = 42 - 13.5 = 28.5 \, \text{kN}\cdot\text{m} \\ M(5 \, \text{m}) &= \frac{47}{3}(6-5) - \frac{3}{2}(6-5)^2 \quad (\text{utilisant la formule depuis la droite pour simplifier}) \\ &= \frac{47}{3}(1) - \frac{3}{2}(1)^2 = \frac{47}{3} - \frac{3}{2} = \frac{94-9}{6} = \frac{85}{6} \, \text{kN}\cdot\text{m} \approx 14.17 \, \text{kN}\cdot\text{m} \end{aligned}

Résultat Question 3 :

Équations de M(x) établies pour chaque section.
Diagramme tracé.
$M(1 \, \text{m}) \approx 15.83 \, \text{kN}\cdot\text{m}$
$M(3 \, \text{m}) = 28.5 \, \text{kN}\cdot\text{m}$
$M(5 \, \text{m}) \approx 14.17 \, \text{kN}\cdot\text{m}$

Question 4 : Point de Moment Maximal ($M_{\text{max}}$)

Principe :

Le moment fléchissant est maximal (ou minimal, c'est-à-dire un extremum) lorsque sa dérivée par rapport à $x$ est nulle. Or, la dérivée du moment fléchissant est l'effort tranchant : $dM/dx = V(x)$. Donc, le moment maximal se produit en un point où l'effort tranchant $V(x)$ est nul ou change de signe.

Analyse et Calcul :

D'après l'analyse de l'effort tranchant (Question 2) :

Dans la section $0 \le x < 2 \, \text{m}$, $V(x)$ ne s'annule pas (il passe de $17.33$ à $11.33 \, \text{kN}$).
Dans la section $2 \le x < 4 \, \text{m}$, $V(x) = \frac{22}{3} - 3x$. Posons $V(x) = 0 \Rightarrow \frac{22}{3} - 3x = 0 \Rightarrow 3x = \frac{22}{3} \Rightarrow x = \frac{22}{9} \, \text{m}$. Comme $2 \le \frac{22}{9} \approx 2.444 \, \text{m} < 4$, ce point est dans la section considérée. C'est ici que se situe le moment maximal.
Dans la section $4 \le x \le 6 \, \text{m}$, $V(x)$ est toujours négatif.

Le moment maximal se produit donc à $x = \frac{22}{9} \, \text{m}$.

Calcul de $M_{\text{max}}$ en utilisant l'équation de $M(x)$ pour la section 2 (valable pour $x = 22/9 \, \text{m}$) :

\begin{aligned} M\left(\frac{22}{9}\right) &= \frac{52}{3}\left(\frac{22}{9}\right) - \frac{3}{2}\left(\frac{22}{9}\right)^2 - 10\left(\frac{22}{9}-2\right) \\ &= \frac{1144}{27} - \frac{3}{2} \cdot \frac{484}{81} - 10\left(\frac{22-18}{9}\right) \\ &= \frac{1144}{27} - \frac{242}{27} - 10\left(\frac{4}{9}\right) \\ &= \frac{902}{27} - \frac{40}{9} \\ &= \frac{902}{27} - \frac{120}{27} \\ &= \frac{782}{27} \, \text{kN}\cdot\text{m} \\ &\approx 28.96 \, \text{kN}\cdot\text{m} \end{aligned}

Résultat Question 4 : Le moment fléchissant maximal se produit à $x = \frac{22}{9} \, \text{m} \approx 2.44 \, \text{m}$ de l'appui gauche, et sa valeur est $M_{\text{max}} = \frac{782}{27} \, \text{kN}\cdot\text{m} \approx 28.96 \, \text{kN}\cdot\text{m}$.

Quiz Intermédiaire 3 : La relation entre l'effort tranchant $V(x)$ et le moment fléchissant $M(x)$ est (avec la convention de signe où une charge vers le bas est négative) :

$V(x) = dM(x)/dx$
$M(x) = dV(x)/dx$
$V(x) = -dM(x)/dx$
Il n'y a pas de relation différentielle directe.

Glossaire

Poutre Simplement Appuyée: Poutre reposant sur deux appuis simples (un appui fixe et un appui mobile ou à rouleau) qui permettent la rotation aux extrémités mais empêchent la translation verticale (et la translation horizontale pour l'appui fixe).
Charge Répartie: Charge agissant sur une certaine longueur de la poutre, exprimée en force par unité de longueur (ex: kN/m).
Charge Ponctuelle (ou Concentrée): Charge agissant en un point spécifique de la poutre, exprimée en force (ex: kN).
Réaction d'Appui: Force exercée par un appui sur la poutre pour la maintenir en équilibre sous l'effet des charges appliquées.
Effort Tranchant ($V(x)$): Somme algébrique des forces transversales (perpendiculaires à l'axe de la poutre) agissant sur la portion de la poutre située à gauche (ou à droite) d'une section donnée. Il représente la tendance de la poutre à cisailler.
Moment Fléchissant ($M(x)$): Somme algébrique des moments des forces externes (charges et réactions) agissant à gauche (ou à droite) d'une section donnée, par rapport à cette section. Il représente la tendance de la poutre à fléchir (se courber).
Diagramme d'Effort Tranchant (DET): Représentation graphique de la variation de l'effort tranchant le long de la poutre.
Diagramme de Moment Fléchissant (DMF): Représentation graphique de la variation du moment fléchissant le long de la poutre.
Équilibre Statique: État d'un corps au repos où la somme de toutes les forces externes agissant sur lui est nulle, et la somme de tous les moments externes par rapport à n'importe quel point est nulle.

4 Commentaires

Evariste Kouame sur 13 avril 2024 à 9h08

J’aime bien ce gens d’exercice
Réponse
Aurélien B. sur 19 mai 2024 à 12h05

Bonjour,
Je suis en BUT GCCD 1ère année et j’ai du mal avec mes exercices de mécanique des structures, pour déterminer Vy ainsi que Mz à toute distance sur la poutre il nous est demandé de les déterminer en fonction de « x », je n’y arrive pas.
On arrive en fin de semestre et je n’ai plus TD mais les partiels arrivent à grand pas, serait-il possible d’en discuter par mail ?

Merci.
Cordialement Aurélien B.
Réponse
- EGC - Génie Civil sur 19 mai 2024 à 17h12
  
  Bonjour, vous pouvez nous écrire directement sur Contact@etudiantgeniecivil.com, Nous serons ravis de vous aider!!!
  Réponse
عبد العاطي السعيدي sur 15 mars 2025 à 10h06

Bien explication dans le calculer de genie civile
Réponse

Calcul l’effort tranchant et le moment

Données de l'étude

Schéma : Poutre Simplement Appuyée avec Charges

Questions à traiter

Correction : Calcul de l’Effort Tranchant et du Moment Fléchissant

Question 1 : Réactions aux Appuis (\(R_A\) et \(R_B\))

Principe :

Formule(s) utilisée(s) :

Données spécifiques :

Calcul :

Question 2 : Effort Tranchant \(V(x)\)

Principe :

a. Équations de l'effort tranchant :

b. Tracé du diagramme de l’effort tranchant (DET) :

Diagramme de l'Effort Tranchant (DET)

c. Calcul de l’effort tranchant à des points spécifiques :

Question 3 : Moment Fléchissant \(M(x)\)

Principe :

a. Équations du moment fléchissant :

b. Tracé du diagramme du moment fléchissant (DMF) :

Diagramme du Moment Fléchissant (DMF)

c. Calcul du moment fléchissant à des points spécifiques :

Question 4 : Point de Moment Maximal (\(M_{\text{max}}\))

Principe :

Analyse et Calcul :

Quiz Rapide : Testez vos connaissances (Récapitulatif)

Glossaire

4 Commentaires

Soumettre un commentaire Annuler la réponse