Études de cas pratique

EGC

Calcul des Dimensions de la Semelle

Calcul des Dimensions d'une Semelle de Fondation Isolée

Comprendre le Dimensionnement des Semelles

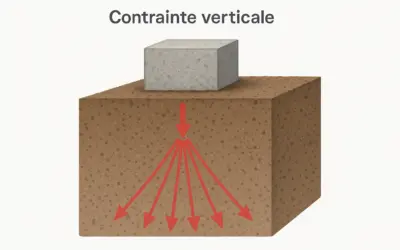
Les semelles de fondation sont des éléments structuraux qui transmettent les charges d'un bâtiment au sol. Leur dimensionnement correct est crucial pour assurer la stabilité de l'ouvrage et éviter les tassements excessifs ou la rupture du sol. L'objectif principal est de répartir la charge sur une surface suffisamment grande pour que la contrainte appliquée au sol (\(\sigma_{sol}\)) ne dépasse pas sa capacité portante admissible (\(q_{adm}\)).

Données de l'étude

On souhaite dimensionner une semelle carrée isolée sous un poteau centré, supportant une charge verticale.

Charges et caractéristiques du sol :

  • Charge verticale permanente et d'exploitation transmise par le poteau à l'état limite de service (ELS) (\(N_{ser}\)) : \(450 \, \text{kN}\).
  • Capacité portante admissible du sol (\(q_{adm}\)) : \(150 \, \text{kPa} = 150 \, \text{kN/m}^2\).
  • On souhaite une semelle carrée de côté \(B\).

Hypothèses : La charge est centrée sur la semelle. Le poids propre de la semelle et des terres au-dessus est négligé dans un premier temps pour simplifier le calcul de la surface (ou considéré comme inclus dans \(N_{ser}\) pour ce niveau d'exercice). On ne vérifie pas le poinçonnement ni les armatures ici, seulement la surface d'appui.

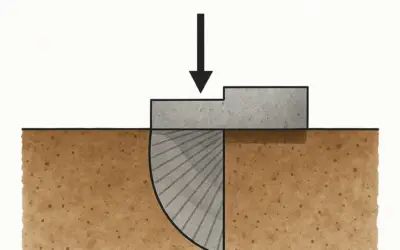
Schéma : Semelle Isolée sous Poteau
Nser Sol (qadm) \(\sigma_{sol}\) B = ? Semelle Carrée Isolée

Schéma d'une semelle carrée isolée sous un poteau avec la charge appliquée et la réaction du sol.

Questions à traiter

  1. Quelle est la condition fondamentale pour dimensionner la surface d'une semelle vis-à-vis de la capacité portante du sol ?
  2. Calculer la surface minimale requise (\(A_{req}\)) pour la semelle.
  3. En déduire la dimension minimale du côté (\(B\)) de la semelle carrée.
  4. Proposer une dimension pratique pour le côté \(B\) (arrondie au 5 cm supérieur).
  5. Vérifier la contrainte effective appliquée par la semelle au sol (\(\sigma_{eff}\)) avec la dimension \(B\) choisie.

Correction : Calcul des Dimensions d'une Semelle

Question 1 : Condition fondamentale de dimensionnement

Principe :

Pour assurer la stabilité et éviter un poinçonnement excessif du sol, la contrainte appliquée par la fondation sur le sol (\(\sigma_{sol}\)) doit être inférieure ou égale à la capacité portante admissible du sol (\(q_{adm}\)). La contrainte au sol est la charge totale divisée par la surface de la semelle.

Formule(s) utilisée(s) :
\[ \sigma_{sol} = \frac{N_{ser}}{A} \le q_{adm} \]
Réponse Question 1 : La condition est que la contrainte exercée par la semelle sur le sol soit inférieure ou égale à la capacité portante admissible du sol (\(\sigma_{sol} \le q_{adm}\)).

Question 2 : Surface minimale requise (\(A_{req}\))

Principe :

À partir de la condition \(\sigma_{sol} \le q_{adm}\), on peut déduire que la surface minimale requise \(A_{req}\) est donnée par \(A_{req} \ge N_{ser} / q_{adm}\). On prendra la valeur minimale pour le calcul.

Formule(s) utilisée(s) :
\[ A_{req} = \frac{N_{ser}}{q_{adm}} \]
Données spécifiques :
  • Charge de service (\(N_{ser}\)) : \(450 \, \text{kN}\)
  • Capacité portante admissible (\(q_{adm}\)) : \(150 \, \text{kN/m}^2\)
Calcul :
\[ \begin{aligned} A_{req} &= \frac{450 \, \text{kN}}{150 \, \text{kN/m}^2} \\ &= 3.0 \, \text{m}^2 \end{aligned} \]
Résultat Question 2 : La surface minimale requise pour la semelle est \(A_{req} = 3.0 \, \text{m}^2\).

Quiz Intermédiaire 1 : Si la capacité portante du sol diminue, la surface requise de la semelle (pour une même charge) :

Question 3 : Dimension minimale du côté (\(B\)) de la semelle carrée

Principe :

Pour une semelle carrée de côté \(B\), la surface est \(A = B^2\). Donc, \(B = \sqrt{A_{req}}\).

Formule(s) utilisée(s) :
\[ B = \sqrt{A_{req}} \]
Données spécifiques :
  • \(A_{req} = 3.0 \, \text{m}^2\)
Calcul :
\[ \begin{aligned} B &= \sqrt{3.0 \, \text{m}^2} \\ &\approx 1.732 \, \text{m} \end{aligned} \]
Résultat Question 3 : La dimension minimale du côté de la semelle carrée est \(B \approx 1.732 \, \text{m}\).

Question 4 : Dimension pratique pour le côté \(B\)

Principe :

En pratique, les dimensions des semelles sont arrondies à des valeurs constructibles, généralement au 5 cm ou 10 cm supérieur.

Données spécifiques (résultat précédent) :
  • \(B_{calculé} \approx 1.732 \, \text{m}\)
Choix :

On arrondit \(1.732 \, \text{m}\) au 5 cm supérieur.

\[ B_{choisi} = 1.75 \, \text{m} \]
Résultat Question 4 : Une dimension pratique pour le côté de la semelle est \(B = 1.75 \, \text{m}\).

Question 5 : Vérification de la contrainte effective (\(\sigma_{eff}\))

Principe :

Avec la dimension choisie \(B_{choisi}\), on calcule la surface réelle de la semelle \(A_{eff} = B_{choisi}^2\), puis la contrainte effective \(\sigma_{eff} = N_{ser} / A_{eff}\). On vérifie ensuite que \(\sigma_{eff} \le q_{adm}\).

Formule(s) utilisée(s) :
\[ A_{eff} = B_{choisi}^2 \] \[ \sigma_{eff} = \frac{N_{ser}}{A_{eff}} \]
Données spécifiques :
  • \(B_{choisi} = 1.75 \, \text{m}\)
  • \(N_{ser} = 450 \, \text{kN}\)
  • \(q_{adm} = 150 \, \text{kN/m}^2\)
Calcul :
\[ \begin{aligned} A_{eff} &= (1.75 \, \text{m})^2 = 3.0625 \, \text{m}^2 \\ \sigma_{eff} &= \frac{450 \, \text{kN}}{3.0625 \, \text{m}^2} \\ &\approx 146.94 \, \text{kN/m}^2 \end{aligned} \]

Vérification :

\[ 146.94 \, \text{kN/m}^2 \le 150 \, \text{kN/m}^2 \quad (\text{OK}) \]
Résultat Question 5 : La contrainte effective est \(\sigma_{eff} \approx 146.94 \, \text{kPa}\), ce qui est inférieur à \(q_{adm} = 150 \, \text{kPa}\). La dimension choisie est donc acceptable.

Quiz Intermédiaire 2 : Si la charge \(N_{ser}\) augmente et que \(q_{adm}\) reste constante, la dimension B de la semelle carrée devra :

Quiz Rapide : Testez vos connaissances (Récapitulatif)

1. La capacité portante admissible du sol (\(q_{adm}\)) est :

2. L'unité de la capacité portante admissible du sol (\(q_{adm}\)) est typiquement :

3. Pour une semelle carrée, si on double la longueur de son côté B, sa surface A :

Glossaire

Semelle de Fondation
Élément de fondation superficielle qui répartit les charges d'un poteau, d'un mur ou d'une structure sur une plus grande surface du sol.
Capacité Portante Admissible (\(q_{adm}\))
Contrainte maximale que le sol peut supporter en toute sécurité, en tenant compte des risques de rupture et de tassements excessifs. Elle est généralement déterminée à partir de la capacité portante ultime du sol divisée par un facteur de sécurité.
Contrainte au Sol (\(\sigma_{sol}\))
Pression exercée par la fondation sur le sol. Pour une charge centrée, elle est égale à la charge totale divisée par la surface de contact de la semelle.
État Limite de Service (ELS)
État pour lequel les conditions d'utilisation normale d'une structure ne sont plus satisfaites (par exemple, déformations excessives, vibrations). Les charges de service sont utilisées pour les vérifications à l'ELS.
kPa (kilopascal)
Unité de pression égale à 1000 Pascals, soit 1 kN/m².
Calcul des Dimensions d'une Semelle - Exercice d'Application

D’autres exercices de fondation :

1 Commentaire
  1. Emery TALO
    Emery TALO sur 9 février 2024 à 10h29

    Bonjour,
    je trouve que le document est très intéressant et je me trouve dans le besoin.

    Merci,
    Cordialement.

    Réponse
Soumettre un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *