Calcul de la longueur de flambement critique
Comprendre le Calcul de la longueur de flambement critique
Dans la conception de structures métalliques, la longueur de flambement critique est une mesure clé qui aide à déterminer la résistance d’une colonne métallique soumise à des charges de compression. Cette longueur est cruciale pour éviter le flambement de la colonne, qui peut entraîner l’effondrement de la structure.
Pour comprendre l’Analyse d’une Poutre en Acier, cliquez sur le lien.
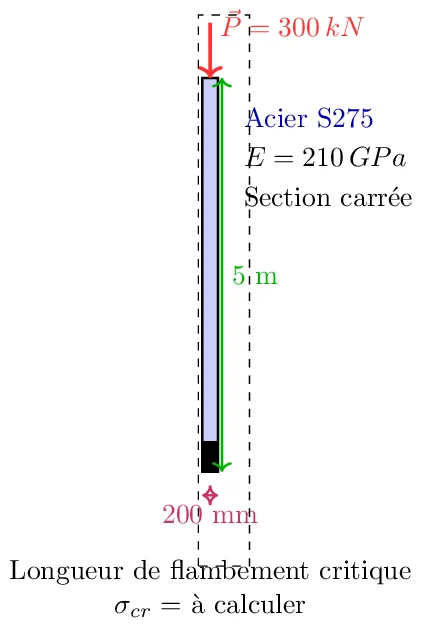
Données:
- Matériau de la colonne: Acier S275
- Section transversale: Carrée, avec une dimension de côté de 200 mm
- Longueur de la colonne: 5 mètres
- Charge axiale appliquée: \( P = 300 \, \text{kN} \)
Propriétés de l’acier S275
- Module d’élasticité (E): 210 GPa
- Contrainte de flambement critique (\(\sigma_{cr}\)): à calculer
Question:
Calculer la longueur de flambement critique (\( L_{cr} \)) pour une colonne en acier S275 avec une section carrée sous une charge axiale donnée, en utilisant la formule de l’Eurocode 3 pour les colonnes élancées.
Correction : Calcul de la longueur de flambement critique
1. Explication
Dans la conception des colonnes en acier, la résistance à la compression est limitée par le risque de flambement. Le flambement se produit lorsque la colonne dévie latéralement sous une charge axiale. Pour une colonne élancée, l’Eurocode 3 propose d’utiliser une relation inspirée de la formule d’Euler.
L’idée est d’exprimer la contrainte de flambement critique (\(\sigma_{cr}\)) en fonction du module d’élasticité (\(E\)), de la géométrie de la section (via le rayon de giration \(r\)) et de la «longueur efficace» ou longueur de flambement critique (\(L_{cr}\)). En égalant cette contrainte à la contrainte induite par la charge appliquée (\(P/A\)), on peut déterminer \(L_{cr}\).
2. Formule
La formule de flambement inspirée d’Euler et utilisée dans l’Eurocode 3 s’exprime sous la forme :
\[ \sigma_{cr} = \frac{\pi^2 E}{\left(\frac{L_{cr}}{r}\right)^2} \]
Or, pour une charge critique \(P_{cr}\), on a :
\[ \sigma_{cr} = \frac{P_{cr}}{A} \]
En posant que la charge appliquée \(P\) correspond à la charge critique, on peut écrire :
\[ \frac{P}{A} = \frac{\pi^2 E}{\left(\frac{L_{cr}}{r}\right)^2} \]
Ce qui, en isolant \(L_{cr}\), donne :
\[ L_{cr} = r \sqrt{\frac{\pi^2 E\, A}{P}} \]
3. Données
Pour cet exercice, les données sont :
Matériau : Acier S275
- Module d’élasticité : \(E = 210 \, \text{GPa} = 210 \times 10^9 \, \text{Pa}\)
Section transversale : Carrée
- Dimension du côté : \(b = 200 \, \text{mm} = 0.2 \, \text{m}\)
- Aire de la section :
\[ A = b^2 = (0.2)^2 = 0.04 \, \text{m}^2 \]
- Moment d’inertie (pour une section carrée) :
\[ I = \frac{b^4}{12} = \frac{(0.2)^4}{12} \] \[ I = \frac{0.0016}{12} \approx 1.33 \times 10^{-4} \, \text{m}^4 \]
Rayon de giration :
\[ r = \sqrt{\frac{I}{A}} = \sqrt{\frac{1.33 \times 10^{-4}}{0.04}} \] \[ r \approx \sqrt{0.00333} \approx 0.05774 \, \text{m} \]
- Charge axiale appliquée : \(P = 300 \, \text{kN} = 300\,000 \, \text{N}\)
4. Calcul
1. Calcul du numérateur de l’expression sous la racine :
\[ \pi^2 \, E \, A \]
- \( \pi^2 \approx 9.8696 \)
- \( E \, A = 210 \times 10^9 \, \text{Pa} \times 0.04 \, \text{m}^2 = 8.4 \times 10^9 \, \text{N/m}^2 \)
Ainsi :
\[ \pi^2 \, E \, A \approx 9.8696 \times 8.4 \times 10^9 \approx 8.2905 \times 10^{10} \, \text{N} \]
2. Division par la charge appliquée \(P\) :
\[ \frac{\pi^2 \, E \, A}{P} = \frac{8.2905 \times 10^{10}}{300\,000} \approx 276348.8 \]
3. Calcul de la racine carrée :
\[ \sqrt{\frac{\pi^2 \, E \, A}{P}} \approx \sqrt{276348.8} \approx 525.7 \]
4. Détermination de \(L_{cr}\) :
\[ L_{cr} = r \times 525.7 \quad \text{où} \quad r \approx 0.05774 \, \text{m} \]
\[ L_{cr} \approx 0.05774 \times 525.7 \] \[ L_{cr} \approx 30.36 \, \text{m} \]
Conclusion
La longueur de flambement critique calculée pour la colonne est d’environ 30,36 mètres.
Ce résultat signifie que, pour une colonne de 5 m de longueur, la charge appliquée de 300 kN reste largement inférieure à la charge critique de flambement théorique. La colonne est donc, du point de vue du flambement, en sécurité.
Calcul de la longueur de flambement critique
D’autres exercices de structure métallique:












0 commentaires