Calcul de la Déflexion Totale

Comprendre le Calcul de la Déflexion Totale

Une poutre horizontale uniforme de longueur L = 6 mètres, de module d’élasticité E = 200 GPa et de moment d’inertie \(I = 300 \times 10^{-6}\) m\(^4\). La poutre est simplement appuyée à ses deux extrémités. Elle subit une charge uniformément répartie \(q = 5\) kN/m sur toute sa longueur.

Pour comprendre le Calcul de flèche d’une poutre, cliquez sur le lien.

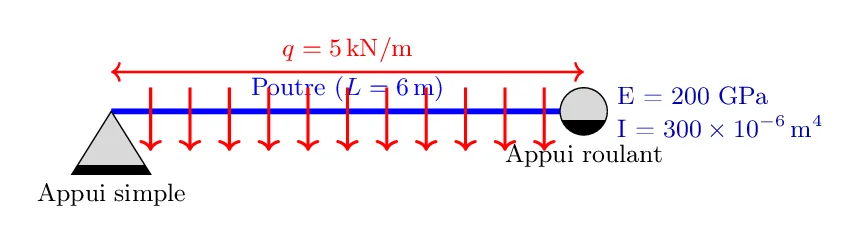
Questions :

1. Calcul de la Réaction aux Appuis :
Déterminer les réactions aux appuis en A et B.

2. Détermination de l’Équation de la Ligne Élastique :
Établir l’équation différentielle de la ligne élastique de la poutre. Résoudre cette équation pour obtenir la forme de la courbe de déflexion de la poutre.

3. Calcul de la Déflexion Maximale :
Calculer la déflexion maximale de la poutre. Identifier sa position le long de la poutre.

4. Analyse de l’Effet d’une Charge Ponctuelle :
Supposer maintenant qu’une charge ponctuelle \(P = 10\) kN est appliquée au milieu de la poutre. Recalculer la déflexion maximale. Comparer cette déflexion à celle obtenue avec la charge uniformément répartie.

Correction : calcul de la Déflexion Totale

On considère une poutre simplement appuyée de longueur

L = 6 m,
avec un module d’élasticité
E = 200 GPa = 200 × 10⁹ N/m²,
et un moment d’inertie
I = 300×10⁻⁶ m⁴ = 0,0003 m⁴.

La poutre est soumise à une charge uniformément répartie de

q = 5 kN/m = 5000 N/m
sur toute sa longueur.

1. Calcul des Réactions aux Appuis

Pour une poutre simplement appuyée et soumise à une charge uniformément répartie, la charge totale est répartie également entre les deux appuis.

Formule et Données:

Charge totale :

\[ Q = q \times L \]

Réaction en A et en B :

\[ R_A = R_B = \frac{Q}{2} = \frac{qL}{2} \]

Données :

\(q = 5000~\text{N/m}\)
\(L = 6~\text{m}\)

Calcul

1. Calcul de la charge totale :

\[ Q = 5000~\text{N/m} \times 6~\text{m} \] \[ Q = 30000~\text{N} \quad (30~\text{kN}) \]

2. Réaction en chaque appui :

\[ R_A = R_B = \frac{30000~\text{N}}{2} = 15000~\text{N} \quad (15~\text{kN}) \]

Résultat

Les réactions aux appuis sont :

\[ R_A = R_B = 15~\text{kN} \]

2. Détermination de l’Équation de la Ligne Élastique

L’équation de la ligne élastique (ou courbe de déflexion) d’une poutre s’obtient à partir de l’équation d’Euler–Bernoulli :

\[ EI\,\frac{d^2y(x)}{dx^2} = M(x) \]

où \( M(x) \) est le moment fléchissant en un point \( x \).

Pour une charge uniformément répartie, le moment à une distance \( x \) du support A est :

\[ M(x) = R_A\,x – \frac{q\,x^2}{2} \]

avec \( R_A = \frac{qL}{2} \). Ainsi :

\[ M(x) = \frac{qL}{2}\,x – \frac{q\,x^2}{2} = \frac{q}{2}\Bigl(Lx – x^2\Bigr) \]

Formulation de l’Équation Différentielle

L’équation différentielle devient :

\[ \frac{d^2y}{dx^2} = \frac{M(x)}{EI} = \frac{q}{2EI}\Bigl(Lx – x^2\Bigr) \]

Première Intégration

On intègre pour obtenir la pente \( \frac{dy}{dx} \) :

\[ \frac{dy}{dx} = \int \frac{q}{2EI}\Bigl(Lx – x^2\Bigr)\,dx = \frac{q}{2EI}\left(\frac{L\,x^2}{2} – \frac{x^3}{3}\right) + C_1 \]

Ce qui s’écrit :

\[ \frac{dy}{dx} = \frac{qL}{4EI}\,x^2 – \frac{q}{6EI}\,x^3 + C_1 \]

Détermination de \( C_1 \) par Symétrie :

La poutre étant symétrique, la pente s’annule au milieu, c’est-à-dire pour \( x = \frac{L}{2} \). Ainsi :

\[ 0 = \frac{qL}{4EI}\left(\frac{L}{2}\right)^2 – \frac{q}{6EI}\left(\frac{L}{2}\right)^3 + C_1 \]

Calculons :

\[ \left(\frac{L}{2}\right)^2 = \frac{L^2}{4},\quad \left(\frac{L}{2}\right)^3 = \frac{L^3}{8} \]

Donc :

\[ 0 = \frac{qL}{4EI}\cdot\frac{L^2}{4} – \frac{q}{6EI}\cdot\frac{L^3}{8} + C_1 = \frac{qL^3}{16EI} – \frac{qL^3}{48EI} + C_1 \] \[ \frac{qL^3}{16EI} – \frac{qL^3}{48EI} = \frac{3qL^3 – qL^3}{48EI} = \frac{2qL^3}{48EI} = \frac{qL^3}{24EI} \]

Ainsi,

\[ C_1 = -\frac{qL^3}{24EI} \]

La pente devient alors :

\[ \frac{dy}{dx} = \frac{qL}{4EI}\,x^2 – \frac{q}{6EI}\,x^3 – \frac{qL^3}{24EI} \]

Deuxième Intégration pour Trouver \( y(x) \)

Intégrons à nouveau pour obtenir la déflexion \( y(x) \) :

\[ y(x) = \int \frac{dy}{dx}\,dx = \int \left[\frac{qL}{4EI}\,x^2 – \frac{q}{6EI}\,x^3 – \frac{qL^3}{24EI}\right] dx + C_2 \]

En intégrant terme à terme :

\[ \int \frac{qL}{4EI}\,x^2\,dx = \frac{qL}{4EI}\cdot\frac{x^3}{3} = \frac{qL}{12EI}\,x^3, \]

\[ \int \frac{q}{6EI}\,x^3\,dx = \frac{q}{6EI}\cdot\frac{x^4}{4} = \frac{q}{24EI}\,x^4, \]

\[ \int \frac{qL^3}{24EI}\,dx = \frac{qL^3}{24EI}\,x. \]

Ainsi :

\[ y(x) = \frac{qL}{12EI}\,x^3 – \frac{q}{24EI}\,x^4 – \frac{qL^3}{24EI}\,x + C_2 \]

En appliquant la condition \( y(0) = 0 \), on obtient \( C_2 = 0 \).

Résultat

L’équation de la ligne élastique est donc :

\[ y(x)=\frac{q}{24EI}\Bigl(2Lx^3 – x^4 – L^3x\Bigr) \]

3. Calcul de la Déflexion Maximale

Pour une poutre simplement appuyée soumise à une charge uniformément répartie, la déflexion maximale se produit au centre, c’est-à-dire en \( x = \frac{L}{2} \).

Une formule standard donne la flèche maximale sous UDL :

\[ y_{\text{max}} = -\frac{5qL^4}{384EI} \]
(le signe négatif indique une déflexion vers le bas).

Données:

\(q = 5000~\text{N/m}\)
\(L = 6~\text{m} \quad \text{donc} \quad L^4 = 6^4 = 1296~\text{m}^4,\)
\(E = 200\times10^9~\text{N/m}^2\)
\(I = 0,0003~\text{m}^4.\)

Calcul

Substituons dans la formule :

\[ y_{\text{max}} = -\frac{5 \times 5000 \times 1296}{384 \times 200\times10^9 \times 0,0003} \] \[ y_{\text{max}} = -\frac{32\,400\,000}{23\,040\,000\,000} \] \[ y_{\text{max}} \approx -0,00140625~\text{m} \]
Ce qui correspond à environ \(-1,41~\text{mm}\).

Résultat

La déflexion maximale de la poutre sous la charge uniformément répartie est :

\[ y_{\text{max}} \approx -1,41~\text{mm} \quad \text{(au centre, } x = 3~\text{m)} \]

4. Analyse de l’Effet d’une Charge Ponctuelle

Situation

On suppose maintenant qu’une charge ponctuelle de

P = 10 kN = 10 000 N
est appliquée au centre de la poutre (en \( x = \frac{L}{2} \)).

Pour une poutre simplement appuyée avec une charge ponctuelle appliquée en son milieu, la flèche maximale est donnée par :

\[ \delta_{\text{max}} = \frac{P\,L^3}{48EI} \]

Données

\(P = 10\,000~\text{N}\)
\(L = 6~\text{m} \quad \text{donc} \quad L^3 = 6^3 = 216~\text{m}^3,\)
\(E = 200\times10^9~\text{N/m}^2\)
\(I = 0,0003~\text{m}^4.\)

Calcul

Numérateur :

\[ P\,L^3 = 10\,000 \times 216 = 2\,160\,000 \]

Dénominateur :

\[ 48EI = 48 \times \left(200\times10^9 \times 0,0003\right) \]

Nous avons déjà calculé :

\[ 200\times10^9 \times 0,0003 = 60\,000\,000 \]

donc :

\[ 48 \times 60\,000\,000 = 2\,880\,000\,000 \]

Ainsi :

\[ \delta_{\text{max}} = \frac{2\,160\,000}{2\,880\,000\,000} \] \[ \delta_{\text{max}} \approx 0,00075~\text{m} = 0,75~\text{mm} \]

Comparaison

Sous charge uniformément répartie : \( y_{\text{max}} \approx 1,41~\text{mm} \) de déflexion.
Sous charge ponctuelle (P = 10 kN) : \( \delta_{\text{max}} \approx 0,75~\text{mm} \) de déflexion.

Interprétation :

La charge uniformément répartie génère une charge totale de \( q \times L = 5~\text{kN/m} \times 6~\text{m} = 30~\text{kN} \) répartie sur toute la poutre, ce qui induit une déflexion maximale plus importante (1,41 mm) que celle produite par une charge ponctuelle de 10 kN (0,75 mm).

Remarque : Pour comparer les effets d’une charge concentrée par rapport à une UDL, il faut tenir compte non seulement de la répartition de la charge mais aussi de la valeur totale appliquée.

Résultat

La déflexion maximale avec la charge ponctuelle de 10 kN est :

\[ \delta_{\text{max}} \approx 0,75~\text{mm} \]

Ainsi, pour cette poutre, la charge uniformément répartie (charge totale de 30 kN) induit une déflexion plus importante que la charge ponctuelle de 10 kN appliquée au milieu.

Calcul de la Déflexion Totale

D’autres exercices de Rdm :