Application de la Méthode des Trois Moments
Comprendre l’Application de la Méthode des Trois Moments
On considère une poutre continue reposant sur trois appuis notés A, B et C. Les dimensions des travées sont les suivantes :
- Travée AB : \( L_1 = 6\,\text{m} \)
- Travée BC : \( L_2 = 4\,\text{m} \)
La poutre est soumise à une charge uniformément répartie de \( q = 5\,\text{kN/m} \) sur les deux travées. On suppose que les appuis A et C sont simplement supportés (donc \( M_A = M_C = 0 \)) et que la continuité est assurée au point B.
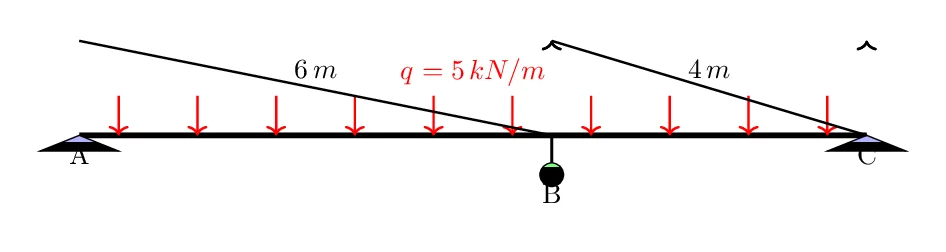
Questions:
1. En appliquant la méthode des trois moments, déterminez le moment fléchissant \( M_B \) à l’appui B.
2. En déduisez, pour chacune des travées, les réactions verticales aux appuis.
Correction : Application de la Méthode des Trois Moments
1. Calcul du moment fléchissant \( M_B \)
1.1. Calcul de l’aire \( A_1 \) pour la travée AB
Pour une poutre simplement supportée sous une charge uniformément répartie, l’aire sous le diagramme de moment est obtenue par:
\[ A_1 = \frac{q L_1^3}{12} \]
Données:
- \( q = 5\,\text{kN/m} \)
- \( L_1 = 6\,\text{m} \)
Calcul:
\[ A_1 = \frac{5 \times 6^3}{12} \] \[ A_1 = \frac{5 \times 216}{12} \] \[ A_1 = \frac{1080}{12} \] \[ A_1 = 90\,\text{kN.m}^2 \]
1.2. Calcul de l’aire \( A_2 \) pour la travée BC
De même, pour la travée BC, on utilise:
\[ A_2 = \frac{q L_2^3}{12} \]
Données:
- \( q = 5\,\text{kN/m} \)
- \( L_2 = 4\,\text{m} \)
Calcul:
\[ A_2 = \frac{5 \times 4^3}{12} \] \[ A_2 = \frac{5 \times 64}{12} \] \[ A_2 = \frac{320}{12} \] \[ A_2 \approx 26.67\,\text{kN.m}^2 \]
1.3. Application de la formule des trois moments pour trouver \( M_B \)
La formule des trois moments est:
\[ \frac{M_A}{L_1} + \frac{2 M_B}{L_1+L_2} + \frac{M_C}{L_2} = -\frac{6}{L_1+L_2}\left(\frac{A_1}{L_1} + \frac{A_2}{L_2}\right) \]
Comme \(M_A = M_C = 0\), elle se simplifie en
\[ \frac{2 M_B}{L_1+L_2} = -\frac{6}{L_1+L_2}\left(\frac{A_1}{L_1} + \frac{A_2}{L_2}\right) \]
Données:
- \( L_1 = 6\,\text{m} \)
- \( L_2 = 4\,\text{m} \) donc \( L_1+L_2 = 10\,\text{m} \)
- \( A_1 = 90\,\text{kN.m}^2 \)
- \( A_2 \approx 26.67\,\text{kN.m}^2 \)
Calcul:
– Calcul de \(\frac{A_1}{L_1}\):
\[ \frac{A_1}{L_1} = \frac{90}{6} = 15\,\text{kN}\cdot\text{m} \]
– Calcul de \(\frac{A_2}{L_2}\):
\[ \frac{A_2}{L_2} = \frac{26.67}{4} \approx 6.667\,\text{kN}\cdot\text{m} \]
– Somme des deux termes :
\[ 15 + 6.667 = 21.667\,\text{kN}\cdot\text{m} \]
– Substitution dans l’équation :
\[ \frac{2 M_B}{10} = -\frac{6}{10} \times 21.667 \]
Simplification en multipliant chaque côté par 10 :
\[ 2 M_B = -6 \times 21.667 = -130.002\,\text{kN}\cdot\text{m} \]
Division par 2 :
\[ M_B = -\frac{130.002}{2} \] \[ M_B\approx -65\,\text{kN}\cdot\text{m} \]
(Le signe négatif indique que le moment est en sens « encoche » selon la convention adoptée.)
2. Calcul des réactions verticales
Nous déterminerons maintenant les réactions dans chacune des travées en utilisant l’équilibre des moments et des forces.
2.1. Travée AB (de A à B)
2.1.1. Calcul de la réaction \( R_B^{(AB)} \) en B (côté AB)
En considérant la travée AB et en appliquant l’équilibre des moments autour de l’appui A, l’équation est:
\[ M_A + R_B^{(AB)} \times L_1 – q L_1 \left(\frac{L_1}{2}\right) = M_B \]
Avec \( M_A = 0 \).
Formule:
\[ R_B^{(AB)} \times L_1 – q L_1 \left(\frac{L_1}{2}\right) = M_B \]
Données:
- \( L_1 = 6\,\text{m} \)
- \( q = 5\,\text{kN/m} \)
- \( M_B = -65\,\text{kN.m} \)
Calcul:
– Charge totale sur la travée AB:
\[q L_1 = 5 \times 6 = 30\,\text{kN} \]
– Distance du centre de gravité de la charge:
\[ \frac{L_1}{2} = \frac{6}{2} = 3\,\text{m} \]
– Moment dû à la charge uniformément répartie:
\[ q L_1 \times \frac{L_1}{2} = 5 \times 6 \times 3 = 90\,\text{kN.m} \]
– Écriture de l’équation:
\[ 6 R_B^{(AB)} – 90 = -65 \]
– Isolement de \( R_B^{(AB)} \):
\[ 6 R_B^{(AB)} = -65 + 90 = 25 \] \[ R_B^{(AB)} = \frac{25}{6} \] \[ R_B^{(AB)} \approx 4.17\,\text{kN}\, \text{(action vers le haut)} \]
2.1.2. Calcul de la réaction \( R_A \) en A
L’équilibre vertical sur la travée AB impose que:
\[ R_A + R_B^{(AB)} = q L_1 \]
Formule:
\[ R_A = q L_1 – R_B^{(AB)} \]
Données:
- \(qL_1 = 5 \times 6 = 30 \, \text{kN}\)
- \(R_B^{(AB)} \approx 4.17 \, \text{kN}\)
Calcul :
\[ R_A = 30 – 4.17 \] \[ R_A \approx 25.83 \, \text{kN}\, \text{(vers le haut)} \]
2.2. Travée BC (de B à C)
2.2.1. Calcul de la réaction \(R_C\) en C
Pour la travée BC, en appliquant l’équilibre des moments autour de l’appui B, on utilise
\[ M_B + R_C \times L_2 – qL_2 \left(\frac{L_2}{2}\right) = M_C \]
Avec \(M_C = 0\)
Formule :
\[ M_B + R_C \times L_2 – qL_2 \left(\frac{L_2}{2}\right) = 0 \]
Données :
- \(L_2 = 4 \, \text{m}\)
- \(q = 5 \, \text{kN/m}\)
- \(M_B = -65 \, \text{kN} \cdot \text{m}\)
- \(M_C = 0\)
Calcul :
– Charge totale sur BC :
\[ qL_2 = 5 \times 4 = 20 \, \text{kN} \]
– Bras de la charge :
\[ \frac{L_2}{2} = 2 \, \text{m} \]
– Moment dû à la charge :
\[ qL_2 \times \frac{L_2}{2} = 5 \times 4 \times 2 = 40 \, \text{kN} \cdot \text{m} \]
– Écriture de l’équation :
\[ -65 + 4 R_C – 40 = 0 \]
– Isolement de \(R_C\) :
\[ 4 R_C = 65 + 40 = 105 \] \[ R_C = \frac{105}{4} \] \[ R_C = 26.25 \, \text{kN}\, \text{(vers le haut)} \]
2.2.2. Calcul de la réaction \(R_B^{(BC)}\) en B (côté BC)
L’équilibre vertical sur la travée BC donne
\[ R_B^{(BC)} + R_C = qL_2 \]
Formule :
\[ R_B^{(BC)} = qL_2 – R_C \]
Données :
- \(qL_2 = 20 \, \text{kN}\)
- \(R_C = 26.25 \, \text{kN}\)
Calcul :
\[ R_B^{(BC)} = 20 – 26.25 \] \[ R_B^{(BC)} = -6.25 \, \text{kN} \]
(Le signe négatif indique que, du côté BC, la réaction en B est dirigée vers le bas.)
2.2.3. Calcul de la réaction totale en B
L’appui B est commun aux deux travées. Sa réaction totale est la somme des contributions issues de la travée AB et de la travée BC.
Formule :
\[ R_B = R_B^{(AB)} + R_B^{(BC)} \]
Données :
- \(R_B^{(AB)} \approx 4.17 \, \text{kN}\)
- \(R_B^{(BC)} \approx -6.25 \, \text{kN}\)
Calcul :
\[ R_B \approx 4.17 + (-6.25) \] \[ R_B= -2.08 \, \text{kN}\, \text{(action dirigée vers le bas)} \]
Application de la Méthode des Trois Moments
D’autres exercices de Rdm:









0 commentaires