Analyse d’une Poutre en Béton Précontraint
Comprendre l’Analyse d’une Poutre en Béton Précontraint
Concevoir une poutre en béton précontraint pour une application spécifique, en utilisant les méthodes de pré-tension et de post-tension, conformément aux Eurocodes.
pour comprendre le Calcul de la Section d’Acier de Précontrainte, cliquez sur le lien.
Données de l’exercice :
- Application : Poutre de pont
- Portée de la poutre : 30 mètres
- Charge permanente (G) : 25 kN/m (y compris le poids de la poutre)
- Charge d’exploitation (Q) : 45 kN/m
- Matériau : Béton de classe C30/37, acier de précontrainte de classe 1570/1770
- Coefficient partiel de sécurité pour le béton (γc) : 1.5
- Coefficient partiel de sécurité pour l’acier (γs) : 1.15

Questions :
1. Analyse des Charges et Moments
- Calculer les charges totales sur la poutre.
- Déterminer les moments de flexion maximaux dus aux charges permanentes et d’exploitation.
2. Conception de la Section en Béton
- Choisir une section transversale appropriée pour la poutre.
- Vérifier la résistance de la section au moment de flexion.
3. Calcul de la Précontrainte
- Déterminer le niveau de précontrainte nécessaire pour contrôler les déformations et les contraintes dans le béton.
- Pour la pré-tension : Calculer la force initiale de précontrainte et les pertes de précontrainte dues à l’élasticité du béton, au fluage, au retrait, etc.
- Pour la post-tension : Définir le profil de câblage et calculer la force de précontrainte à appliquer.
4. Vérifications selon Eurocode
- Vérifier la contrainte dans le béton et l’acier de précontrainte sous les combinaisons de charges ultimes et de service, selon les Eurocodes.
- Assurer que les contraintes et les déformations sont dans les limites permises.
5. Dessin Technique
- Fournir un dessin technique de la poutre, indiquant la disposition des câbles de précontrainte, les dimensions de la section, et les armatures complémentaires si nécessaire.
Correction : Analyse d’une Poutre en Béton Précontraint
1. Analyse des Charges et Moments
1.1 Calcul des charges totales (combinaison ultime)
On combine la charge permanente (\(G\)) et la charge d’exploitation (\(Q\)) en appliquant les coefficients partiels usuels pour l’ultime (selon Eurocode, souvent 1.35 pour \(G\) et 1.5 pour \(Q\)).
Formule :
\[ q_u = 1.35 \times G + 1.5 \times Q \]
Données :
- \(G = 25\ \text{kN/m}\)
- \(Q = 45\ \text{kN/m}\)
Calcul :
1. Calcul de la contribution de \(G\) :
\[ 1.35 \times 25\ \text{kN/m} = 33.75\ \text{kN/m} \]
2. Calcul de la contribution de \(Q\) :
\[ 1.5 \times 45\ \text{kN/m} = 67.5\ \text{kN/m} \]
3. Somme totale :
\[ q_u = 33.75 + 67.5 = 101.25\ \text{kN/m} \]
1.2 Calcul du moment fléchissant maximal
Pour une poutre simplement supportée soumise à une charge uniformément répartie, le moment fléchissant maximal se trouve au milieu de la portée et est donné par
\[ M_u = \frac{q_u \times L^2}{8} \]
Données :
- \(q_u = 101.25\ \text{kN/m}\)
- Portée \(L = 30\ \text{m}\)
Calcul :
1. Calcul de \(L^2\) :
\[ L^2 = 30^2 = 900\ \text{m}^2 \]
2. Multiplication par \(q_u\) :
\[ 101.25\ \text{kN/m} \times 900\ \text{m}^2 = 91125\ \text{kN}\cdot\text{m} \]
3. Division par 8 :
\[ M_u = \frac{91125}{8} = 11390.625\ \text{kN}\cdot\text{m} \]
1.3 Décomposition des moments individuels
Pour la charge permanente (\(G\)) :
Formule :
\[ M_{G} = \frac{1.35 \times G \times L^2}{8} \]
Calcul :
- \(1.35 \times 25 = 33.75\ \text{kN/m}\)
\[ M_{G} = \frac{33.75 \times 900}{8} \] \[ M_{G} = \frac{30375}{8} \] \[ M_{G} = 3796.875\ \text{kN}\cdot\text{m} \]
Pour la charge d’exploitation (\(Q\)) :
Formule :
\[ M_{Q} = \frac{1.5 \times Q \times L^2}{8} \]
Calcul :
- \(1.5 \times 45 = 67.5\ \text{kN/m}\)
\[ M_{Q} = \frac{67.5 \times 900}{8} \] \[ M_{Q} = \frac{60750}{8} \] \[ M_{Q} = 7593.75\ \text{kN}\cdot\text{m} \]
Vérification :
\( M_G + M_Q = 3796.875 + 7593.75 = 11390.625\ \text{kN}\cdot\text{m}\) (correspond à \(M_u\)).
2. Conception de la Section en Béton
2.1 Choix de la section
Pour une poutre de pont de portée 30 m, il est fréquent de choisir une section suffisamment robuste. Dans cet exemple, nous adoptons une section rectangulaire avec :
- Largeur \(b = 1.0\ \text{m}\)
- Hauteur totale \(H = 2.0\ \text{m}\)
- Profondeur efficace \(d = 2.0\ \text{m}\) (après déduction de la couverture minimale).
2.2 Vérification de la résistance en flexion par précontrainte
En précontrainte, le moment résistant \(M_{Rd}\) est principalement fourni par la force de précontrainte \(P\) agissant avec un levier effectif \(z\). On a :
\[ M_{Rd} = P \times z \]
Pour assurer la sécurité, il faut que \(M_{Rd} \geq M_u\).
Une estimation courante consiste à prendre \(z \approx 0.9 \times d\).
Données :
- \(d = 2.0\ \text{m}\)
- Estimation : \(z \approx 0.9 \times 2.0 = 1.8\ \text{m}\)
Calcul du \(P\) requis (estimation initiale) :
\[ P_{\text{req}} = \frac{M_u}{z} = \frac{11390.625\ \text{kN}\cdot\text{m}}{1.8\ \text{m}} \] \[ P_{\text{req}} \approx 6328.125\ \text{kN} \]
2.3 Vérification par calcul de la zone comprimée
Pour vérifier le levier effectif, on détermine la profondeur \(a\) de la zone de compression dans le béton. On utilise la formule :
\[ a = \frac{P_{\text{req}}}{0.85 \times f_{cd} \times b} \]
avec
\[
f_{cd} = \frac{f_{ck}}{\gamma_c}
\]
Données :
- Béton de classe \(C30/37\) : \(f_{ck} = 30\ \text{MPa}\)
- Coefficient de sécurité pour le béton (\(\gamma_c\)) : \(1.5\)
\(\Rightarrow f_{cd} = \frac{30}{1.5} = 20\ \text{MPa}\) - \(b = 1.0\ \text{m}\)
- \(P_{\text{req}} = 6328.125\ \text{kN}\)
Attention aux unités :
- \(1\ \text{MPa} = 1\ \text{N/mm}^2\)
- \(20\ \text{MPa} = 20 \times 10^6\ \text{N/m}^2 = 20000\ \text{kN/m}^2\)
- \(P_{\text{req}} = 6328.125\ \text{kN}\)
Calcul :
\[ a = \frac{6328.125\ \text{kN}}{0.85 \times 20000\ \text{kN/m}^2 \times 1.0\ \text{m}} \] \[ a = \frac{6328.125}{17000} \approx 0.372\ \text{m} \]
Calcul du levier effectif exact :
\[ z = d – \frac{a}{2} \] \[ z = 2.0\ \text{m} – \frac{0.372\ \text{m}}{2} \] \[ z = 2.0\ \text{m} – 0.186\ \text{m} \] \[ z = 1.814\ \text{m} \]
On peut alors recalculer \(P_{\text{req}}\) précisément :
\[ P_{\text{req}} = \frac{M_u}{z} \] \[ P_{\text{req}} = \frac{11390.625\ \text{kN}\cdot\text{m}}{1.814\ \text{m}} \] \[ P_{\text{req}} \approx 6284\ \text{kN} \]
Pour la suite, nous utiliserons \(P_{\text{req}} \approx 6300\ \text{kN}\) (arrondi) comme force de précontrainte nécessaire.
3. Calcul de la Précontrainte
3.1 Détermination de la force de précontrainte requise
La force de précontrainte doit être telle que, lorsqu’elle est multipliée par le levier effectif \(z\), elle compense le moment ultime appliqué sur la poutre.
Formule :
\[ P_{\text{req}} = \frac{M_u}{z} \]
Données :
- \(M_u = 11390.625\ \text{kN}\cdot\text{m}\)
- \(z \approx 1.814\ \text{m}\)
Calcul :
\[ P_{\text{req}} = \frac{11390.625}{1.814} \approx 6284\ \text{kN} \]
(arrondi, nous utiliserons 6300 kN pour simplifier la suite)
3.2 Pour la pré-tension
En cas de pré-tension, des pertes (par élasticité, fluage, retrait, etc.) réduisent la force effective au service. On suppose un taux de perte de 20 % (soit 0,20).
Formule :
\[ P_{\text{initial}} = \frac{P_{\text{req}}}{1 – \delta_{\text{pertes}}} \]
Données :
- \(P_{\text{req}} \approx 6300\ \text{kN}\)
- \(\delta_{\text{pertes}} = 0.20\)
Calcul :
\[ P_{\text{initial}} = \frac{6300}{1 – 0.20} \] \[ P_{\text{initial}} = \frac{6300}{0.80} \] \[ P_{\text{initial}} = 7875\ \text{kN} \]
3.3 Pour la post-tension
En post-tension, le processus de mise en tension permet de réduire les pertes. On prendra ici un taux de perte de 15 % (soit 0,15).
Formule :
\[ P_{\text{initial}} = \frac{P_{\text{req}}}{1 – \delta_{\text{pertes}}} \]
Données :
- \(P_{\text{req}} \approx 6300\ \text{kN}\)
- \(\delta_{\text{pertes}} = 0.15\)
Calcul :
\[ P_{\text{initial}} = \frac{6300}{1 – 0.15} \] \[ P_{\text{initial}} = \frac{6300}{0.85} \] \[ P_{\text{initial}} \approx 7411.76\ \text{kN} \]
3.4 Calcul de l’aire requise de l’acier de précontrainte
L’aire d’acier nécessaire se détermine en s’assurant que la contrainte dans l’acier ne dépasse pas la limite de calcul \(f_{pd}\). On a :
\[ A_s = \frac{P_{\text{req}}}{f_{pd}} \]
avec
\[ f_{pd} = \frac{f_{pk}}{\gamma_s} \]
Données :
- Pour l’acier de classe 1570, on prend \(f_{pk} = 1570\ \text{MPa}\)
- Coefficient partiel pour l’acier (\(\gamma_s\)) : \(1.15\)
\(\Rightarrow f_{pd} = \frac{1570}{1.15} \approx 1365.22\ \text{MPa}\) - \(P_{\text{req}} \approx 6300\ \text{kN} = 6\,300\,000\ \text{N}\)
- Attention : \(1\ \text{MPa} = 1\ \text{N/mm}^2\)
Calcul :
\[ A_s = \frac{6\,300\,000\ \text{N}}{1365.22\ \text{N/mm}^2} \] \[ A_s \approx 4615\ \text{mm}^2 \]
4. Vérifications selon Eurocode
4.1 Vérification de la contrainte dans le béton
La vérification consiste à s’assurer que la contrainte compressive induite par la force de précontrainte ne dépasse pas la limite admissible.
La contrainte moyenne dans la section (en utilisant l’aire de la section) est :
\[ \sigma_c = \frac{P_{\text{req}}}{A_c} \]
avec \(A_c = b \times d\).
Données :
- \(b = 1.0\ \text{m}\)
- \(d = 2.0\ \text{m}\), donc \(A_c = 1.0 \times 2.0 = 2.0\ \text{m}^2\)
- \(P_{\text{req}} \approx 6300\ \text{kN}\)
Calcul :
\[ \sigma_c = \frac{6300\ \text{kN}}{2.0\ \text{m}^2} = 3150\ \text{kN/m}^2 \]
Pour convertir en MPa (1 MPa = 1 N/mm\(^2\) = 1000 kN/m\(^2\)) :
\[ 3150\ \text{kN/m}^2 = 3.15\ \text{MPa} \]
Vérification :
La valeur \(3.15\ \text{MPa}\) est bien inférieure à \(f_{cd} = 20\ \text{MPa}\) (et même à \(0.85 \times f_{cd} = 17\ \text{MPa}\)), ce qui est conforme.
4.2 Vérification des contraintes dans l’acier de précontrainte
La contrainte dans l’acier, une fois la force de précontrainte appliquée, ne doit pas excéder \(f_{pd}\).
Par construction, en choisissant l’aire \(A_s\) telle que
\[ A_s = \frac{P_{\text{req}}}{f_{pd}} \]
la contrainte obtenue est :
\[ \sigma_s = \frac{P_{\text{req}}}{A_s} = f_{pd} \]
Ce qui est en accord avec la limite de calcul.
5. Dessin Technique (Schématisation)
Le dessin technique devra représenter la géométrie de la poutre et la disposition des câbles de précontrainte (ou gaines pour le post-tension).
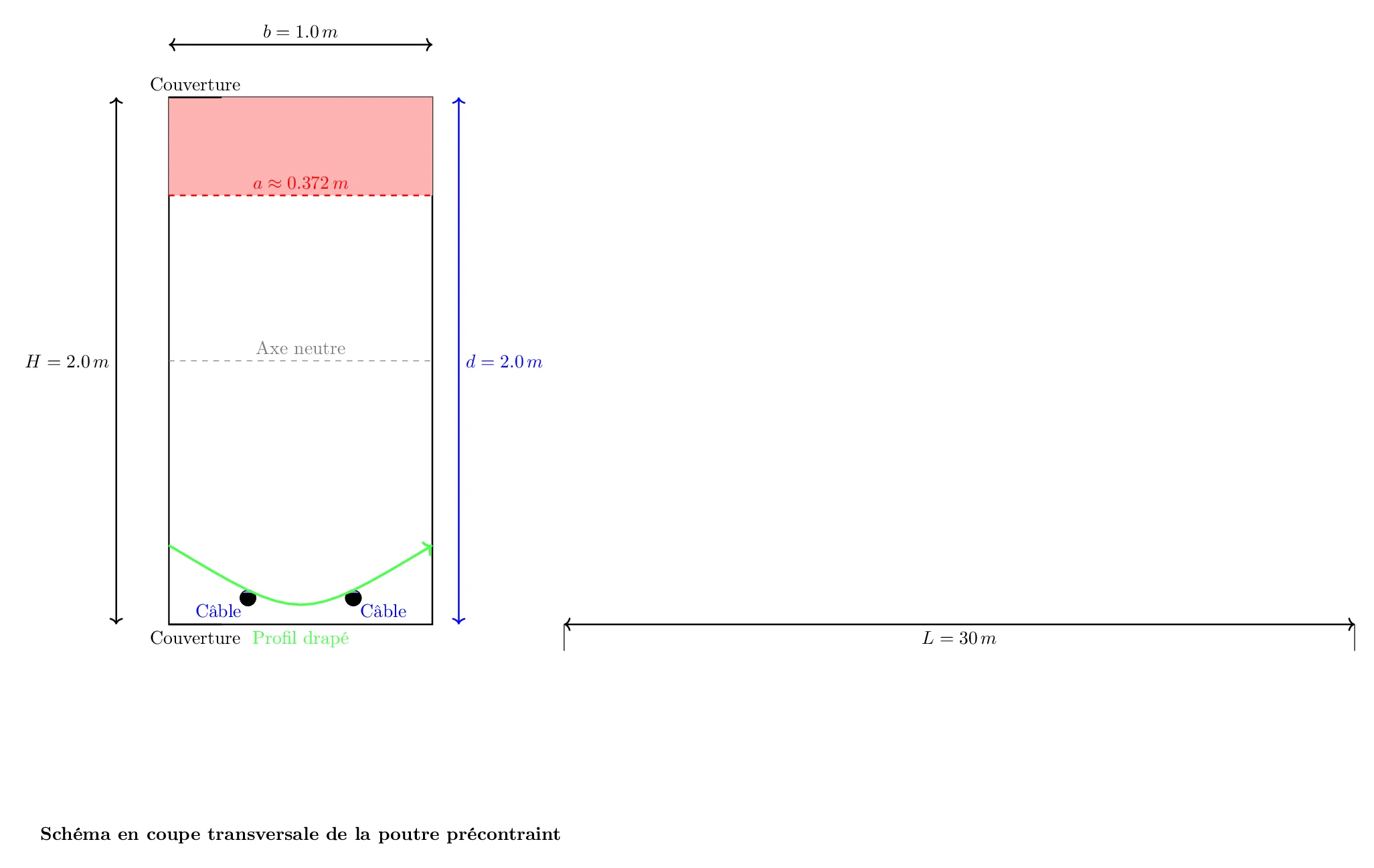
Analyse d’une Poutre en Béton Précontraint
D’autres exercices de béton armé et béton précontraint:










0 commentaires