Calcul des charges concentrées

Comprendre le calcul des charges concentrées

Vous travaillez en tant qu’ingénieur dans une entreprise qui conçoit des poutres en acier pour différents projets de construction. On vous donne la responsabilité de vérifier la capacité d’une poutre à résister à une série de charges concentrées.

Pour comprendre le Comportement en flexion d’une poutre, cliquez sur le lien.

Données :

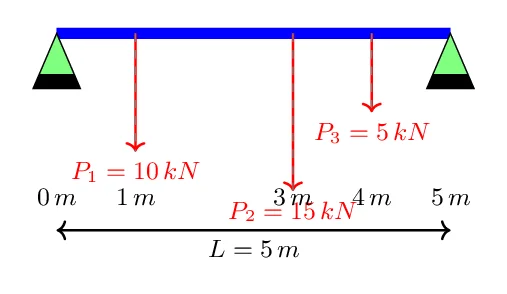
Longueur de la poutre, \(L = 5\) m
Moment d’inertie de la section, \(I = 5000\) cm\(^4\)
Modulus d’élasticité de l’acier, \(E = 210\) GPa
Charges concentrées:

– \(P_1 = 10\) kN à \(a_1 = 1\) m de l’extrémité gauche

– \(P_2 = 15\) kN à \(a_2 = 3\) m de l’extrémité gauche

– \(P_3 = 5\) kN à \(a_3 = 4\) m de l’extrémité gauche

Questions :

1. Calculez les réactions aux appuis si la poutre est simplement appuyée à ses deux extrémités.

2. Tracez le diagramme des moments fléchissants pour toute la longueur de la poutre.

3. Déterminez la position et la valeur du moment fléchissant maximal.

4. En utilisant la formule \(\sigma = \frac{M}{S}\), où \(S\) est le module de la section (en cm\(^3\)), calculez la contrainte maximale dans la poutre si le module de la section est \(S = 250\) cm\(^3\).

Indications :

Pour calculer les réactions aux appuis, utilisez le principe de l’équilibre en considérant les moments et les forces verticales.
Pour le diagramme des moments fléchissants, commencez par les charges concentrées et additionnez les effets successifs.
Rappelez-vous que la contrainte est maximale là où le moment fléchissant est maximal.

Correction : Calcul des charges concentrées

1. Calcul des réactions aux appuis

Pour une poutre simplement appuyée, il faut satisfaire l’équilibre global en considérant :

La somme des forces verticales égale à zéro
La somme des moments (par exemple par rapport à l’appui gauche) égale à zéro

Formule

Équilibre vertical :

\[ R_A + R_B = P_1 + P_2 + P_3 \]

Équilibre des moments (par rapport à A) :

\[ R_B \times L – \big(P_1 \times a_1 + P_2 \times a_2 + P_3 \times a_3\big) = 0 \]

Données

Longueur de la poutre : \( L = 5\, \text{m} \)
Charges concentrées :

– \( P_1 = 10\, \text{kN} \) à \( a_1 = 1\, \text{m} \)
– \( P_2 = 15\, \text{kN} \) à \( a_2 = 3\, \text{m} \)
– \( P_3 = 5\, \text{kN} \) à \( a_3 = 4\, \text{m} \)

Calcul

1. Somme des charges :

\[ R_A + R_B = 10 + 15 + 5 \] \[ R_A + R_B = 30\, \text{kN} \]

2. Moment par rapport à A :

Calcul des moments des charges par rapport à A :

\[ P_1 \times a_1 = 10 \times 1 = 10\, \text{kN}\cdot\text{m} \]

\[ P_2 \times a_2 = 15 \times 3 = 45\, \text{kN}\cdot\text{m} \]

\[ P_3 \times a_3 = 5 \times 4 = 20\, \text{kN}\cdot\text{m} \]

Somme des moments :

\[ \sum M_A = 10 + 45 + 20 = 75\, \text{kN}\cdot\text{m} \]

Équation du moment :

\[ R_B \times 5 = 75 \quad \Longrightarrow \quad R_B = \frac{75}{5} = 15\, \text{kN} \]

3. Détermination de \( R_A \) :

\[ R_A = 30 – 15 \] \[ R_A = 15\, \text{kN} \]

Résultat :

\( R_A = 15\, \text{kN} \)
\( R_B = 15\, \text{kN} \)

2. Diagramme des moments fléchissants

Le moment fléchissant \( M(x) \) à une position \( x \) sur la poutre est obtenu en cumulant les effets de la réaction à gauche et en retranchant les effets des charges concentrées qui sont appliquées avant \( x \). Pour chaque segment, l’expression s’écrit :

\[ M(x) = R_A \times x – \sum_{a_i < x} P_i \times (x – a_i) \]

Formules et intervalles

Segment 1 : \( 0 \le x < 1\, \text{m} \)

Aucune charge n’est encore appliquée.

\[ M(x) = 15\,x \]

À \( x = 1\, \text{m} \) :

\[ M(1) = 15 \times 1 \] \[ M(1) = 15\, \text{kN}\cdot\text{m} \]

Segment 2 : \( 1 \le x < 3\, \text{m} \)

La charge \(P_1\) agit dès \(x \ge 1\, \text{m}\).

\[ M(x) = 15\,x – 10\,(x – 1) \]

À \( x = 3\, \text{m} \) :

\[ M(3) = 15\times3 – 10\,(3-1) \] \[ M(3) = 45 – 20 \] \[ M(3) = 25\, \text{kN}\cdot\text{m} \]

Segment 3 : \( 3 \le x < 4\, \text{m} \)

Les charges \(P_1\) et \(P_2\) sont appliquées.

\[ M(x) = 15\,x – 10\,(x – 1) – 15\,(x – 3) \]

À \( x = 4\, \text{m} \) :

\[ M(4) = 15\times4 – 10\,(4-1) – 15\,(4-3) \] \[ M(4) = 60 – 30 – 15 \] \[ M(4) = 15\, \text{kN}\cdot\text{m} \]

Segment 4 : \( 4 \le x \le 5\, \text{m} \)

Toutes les charges \(P_1\), \(P_2\) et \(P_3\) sont appliquées.

\[ M(x) = 15\,x – 10\,(x – 1) – 15\,(x – 3) – 5\,(x – 4) \]

À \( x = 5\, \text{m} \) (appui droit, moment nul) :

\[ M(5) = 15\times5 – 10\,(5-1) – 15\,(5-3) – 5\,(5-4) \] \[ M(5) = 75 – 40 – 30 – 5 \] \[ M(5) = 0\, \text{kN}\cdot\text{m} \]

Diagramme

Le diagramme des moments fléchissants est donc constitué de segments linéaires reliant les points suivants :

\( (0, 0) \)
\( (1, 15) \)
\( (3, 25) \)
\( (4, 15) \)
\( (5, 0) \)

3. Moment fléchissant maximal

Pour déterminer le moment maximal, on étudie les expressions de \( M(x) \) dans chaque segment. Ici, la valeur maximale apparaît aux frontières des segments ou au point de rupture de la formule.

Calcul

Dans le segment [0, 1] : \( M(1) = 15\, \text{kN}\cdot\text{m} \)
Dans le segment [1, 3] :
\(M(x) = 15\,x – 10\,(x-1) = 5\,x + 10\) (fonction croissante, donc à \(x=3\))

\[ M(3) = 5\times3 + 10 \] \[ M(3) = 25\, \text{kN}\cdot\text{m} \]

Dans le segment [3, 4] :

\(M(x) = -10\,x + 55\) (fonction décroissante, la valeur maximale se trouve encore à \(x=3\))

\[ M(3) = -10\times3 + 55 \] \[ M(3) = 25\, \text{kN}\cdot\text{m} \]

Dans le segment [4, 5] :

La valeur maximale est à \( x=4 \) :

\[ M(4) = 15\, \text{kN}\cdot\text{m} \]

Résultat :
Le moment fléchissant maximal est de 25 kN·m et il se situe à \( x = 3\, \text{m} \) de l’extrémité gauche.

4. Calcul de la contrainte maximale dans la poutre

La contrainte due au moment fléchissant dans une section de poutre est calculée par la formule :

\[ \sigma = \frac{M}{S} \]

où :

\( M \) est le moment fléchissant (à utiliser en unités compatibles)
\( S \) est le module de la section

Données

\( M_{\text{max}} = 25\, \text{kN}\cdot\text{m} \)
Module de la section : \( S = 250\, \text{cm}^3 \)

Conversion des unités pour être compatibles :

1. Convertir \( M_{\text{max}} \) en \( \text{N}\cdot\text{mm} \) :

\[ 25\, \text{kN}\cdot\text{m} = 25\,000\, \text{N}\cdot\text{m} \] \[ = 25\,000\, \text{N}\cdot 1\,000\, \text{mm} = 25\,000\,000\, \text{N}\cdot\text{mm} \]

2. Convertir \( S \) en \( \text{mm}^3 \) :

Sachant que \( 1\, \text{cm}^3 = 1\,000\, \text{mm}^3 \) :

\[ S = 250\, \text{cm}^3 = 250 \times 1\,000 \] \[ = 250\,000\, \text{mm}^3 \]