Calcul des Connexions Métalliques
Comprendre le Calcul des Connexions Métalliques
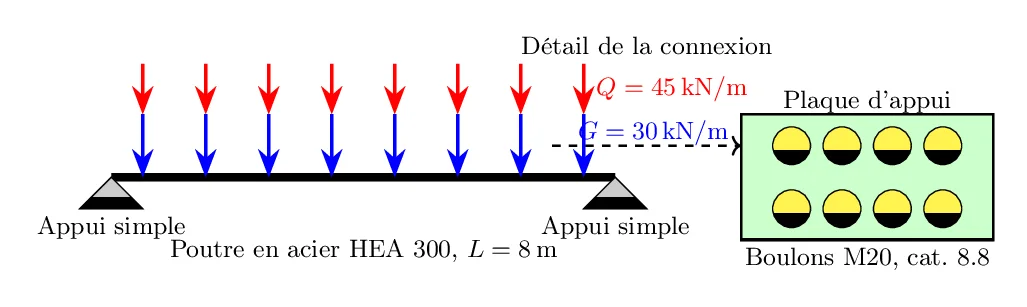
Vous êtes un ingénieur en structure chargé de concevoir une connexion boulonnée pour une poutre en acier dans un bâtiment commercial. La poutre doit supporter une charge uniformément répartie.
Pour comprendre le Calcul du nombre total de boulons nécessaires, cliquez sur le lien.
Les spécifications sont les suivantes :
Données:
- Charge permanente (G) : 30 kN/m
- Charge variable (Q) : 45 kN/m
- Longueur de la poutre (L) : 8 m
- Profil de la poutre : HEA 300
- Matériau : Acier S355
- Type de connexion : Connexion boulonnée avec des boulons de catégorie 8.8
Questions :
1. Calculer les forces internes maximales agissant sur la connexion.
2. Déterminer la taille et le nombre de boulons nécessaires.
3. Vérifier la résistance de la connexion selon l’Eurocode 3.
Correction : Calcul des Connexions Métalliques
Données de l’exercice
- Charge permanente (G) : 30 kN/m
- Charge variable (Q) : 45 kN/m
- Longueur de la poutre (L) : 8 m
- Profil de la poutre : HEA 300
- Matériau : Acier S355
- Type de connexion : Connexion boulonnée (boulons de catégorie 8.8)
- Hypothèses sur les boulons M20 (cat. 8.8) :
– Surface de section effective : \( A_t \approx 245\;\text{mm}^2 \)
– Résistance en traction (fournie par le fabricant ou calculée) :
\[ F_{t,b,Rk} = \frac{A_t \cdot f_{ub}}{\gamma_{M2}} \] \[ F_{t,b,Rk} = \frac{245\;\text{mm}^2 \times 800\;\text{MPa}}{1.25} \] \[ F_{t,b,Rk} \approx 156.8\;\text{kN} \]
– Pour la vérification en cisaillement, on adopte une capacité conservatrice d’environ :
\[ V_{b,Rd} \approx 60\;\text{kN}\quad(\text{par boulon}) \]
1. Calcul des forces internes maximales
1.1. Détermination de la charge de conception
En combinant les charges selon une combinaison UL (exemple courant) :
\[ q = 1.35\,G + 1.5\,Q \]
Substitution des valeurs :
\[ q = 1.35 \times 30 + 1.5 \times 45 \] \[ q = 40.5 + 67.5 \] \[ q = 108\;\text{kN/m} \]
1.2. Calcul de la force de cisaillement maximale
Pour une poutre simplement appuyée soumise à une charge uniformément répartie, la force de cisaillement maximale se situe aux appuis et est donnée par :
\[ V_{\max} = \frac{q\,L}{2} \]
En substituant :
\[ V_{\max} = \frac{108\;\text{kN/m} \times 8\;\text{m}}{2} \] \[ V_{\max} = \frac{864\;\text{kN}}{2} = 432\;\text{kN} \]
1.3. Calcul du moment fléchissant maximal
Le moment maximal, qui se situe en milieu de portée, est :
\[ M_{\max} = \frac{q\,L^2}{8} \]
Substitution :
\[ M_{\max} = \frac{108\;\text{kN/m} \times 8^2}{8} \] \[ M_{\max} = \frac{108 \times 64}{8} \] \[ M_{\max} = \frac{6912}{8} = 864\;\text{kN}\cdot\text{m} \]
2. Détermination de la taille et du nombre de boulons nécessaires
2.1. Vérification en cisaillement
Chaque boulon M20 (cat. 8.8) est supposé offrir une résistance au cisaillement d’environ 60\,kN.
Le nombre de boulons requis pour résister à la force de cisaillement \(V_{\max}\) est alors calculé par :
\[ n = \frac{V_{\max}}{V_{b,Rd}} = \frac{432\;\text{kN}}{60\;\text{kN}} \approx 7,2 \]
On arrondit toujours au nombre entier supérieur pour la sécurité :
\[ n = 8\;\text{boulons} \]
Ces 8 boulons seront répartis de manière symétrique dans la connexion (par exemple, 2 rangées de 4) afin d’assurer une bonne distribution des forces.
3. Vérification de la résistance de la connexion en flexion
Dans une connexion soumise à un moment, la résistance totale est assurée par :
- Le groupe de boulons (les extrémités de la distribution étant en tension et compression), et
- La capacité en flexion de la plaque d’appui.
Hypothèse de travail :
On considère ici que le moment est principalement transféré par les forces de traction dans les boulons situés dans la zone en tension. Pour une répartition symétrique, la moitié des 8 boulons (soit 4) est en tension.
La résistance en flexion fournie par le groupe de boulons peut être exprimée par :
\[ M_R = n_t \times F_{t,b,Rk} \times z \]
où :
- \( n_t = \frac{n}{2} = \frac{8}{2} = 4 \) (nombre de boulons en tension),
- \( F_{t,b,Rk} \approx 156.8\;\text{kN} \) (capacité en traction d’un boulon),
- \( z \) est le bras effectif entre les lignes de boulons (exprimé en mm ou m).
Objectif : Pour résister au moment maximal \( M_{\max} \), il faut :
\[ M_R \ge M_{\max} \]
En exprimant \( z \) (en m) :
\[ 4 \times 156.8\;\text{kN} \times z \ge 864\;\text{kN}\cdot\text{m} \]
Isolons \( z \) :
\[ z \ge \frac{864}{4 \times 156.8} = \frac{864}{627.2} \approx 1.38\;\text{m} \]
Interprétation :
Pour que la partie de la connexion assurée par les boulons puisse, à elle seule, résister au moment de 864 kN·m, il faudrait obtenir un bras effectif d’environ 1,38 m.
Dans la pratique, la conception complète de la connexion ne repose pas uniquement sur la résistance des boulons en traction ; la plaque d’appui et, le cas échéant, des renforts (découpages, nervures) participent également à la résistance au moment.
Le dimensionnement de la plaque doit donc être réalisé de façon à obtenir ce bras effectif (par exemple, en choisissant une plaque suffisamment large et épaisse ou en aménageant une configuration « en portique ») et à vérifier que les sollicitations (traction, compression et actions localisées) restent dans les limites prescrites par l’Eurocode 3.
Remarque finale :
Les calculs ci‑présentés sont simplifiés pour illustrer la démarche. En pratique, la conception détaillée d’une connexion boulonnée tient compte de nombreux autres paramètres (effets combinés, vérifications locales, tolérances de fabrication, etc.) et nécessite souvent l’utilisation de méthodes de calcul plus élaborées ou de logiciels spécialisés.
Calcul des Connexions Métalliques
D’autres exercices de structure métallique:







0 commentaires