Cisaillement dans une poutre

Comprendre le cisaillement dans une poutre

Vous êtes ingénieur en structure et vous devez analyser une poutre en acier simplement appuyée qui supporte une charge uniformément répartie ainsi que des charges concentrées. L’objectif est de déterminer la contrainte de cisaillement maximale dans la poutre.

Pour comprendre la Déformation Axiale Due à la Température, cliquez sur le lien.

Données de l’Exercice

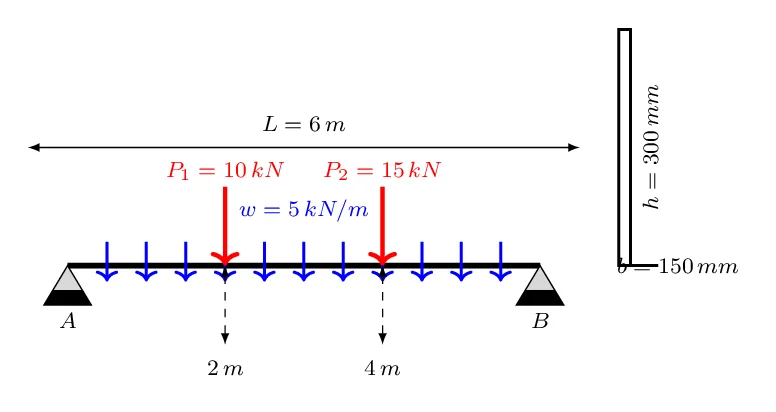
Longueur de la poutre, \( L = 6 \) mètres
Charge uniformément répartie, \( w = 5 \) kN/m
Charges concentrées : \( P_1 = 10 \) kN à 2 m du support gauche, \( P_2 = 15 \) kN à 4 m du support gauche
Largeur de la section transversale de la poutre, \( b = 150 \) mm
Hauteur de la section transversale de la poutre, \( h = 300 \) mm
La poutre est en acier avec une limite d’élasticité de 250 MPa

Questions:

1. Calcul des Réactions aux Appuis :

Déterminez les réactions aux appuis en considérant les charges appliquées.

2. Diagramme de Cisaillement :

Construisez le diagramme de cisaillement de la poutre. Identifiez les points où le cisaillement est maximal.

3. Calcul de la Contrainte de Cisaillement :

Utilisez la formule de cisaillement, \(\tau = \frac{VQ}{Ib}\), où \( V \) est la force de cisaillement, \( Q \) est le moment statique de la zone au-dessus du point d’intérêt, \( I \) est le moment d’inertie de la section transversale, et \( b \) est la largeur de la poutre. Calculez la contrainte de cisaillement maximale dans la poutre.

4. Vérification de la Sécurité :

Comparez la contrainte de cisaillement maximale trouvée avec la limite d’élasticité de l’acier.
Vérifiez si la poutre est sûre pour les charges données.

Correction : cisaillement dans une poutre

1. Calcul des Réactions aux Appuis

Données :

Longueur de la poutre : \(L = 6\) m
Charge uniformément répartie : \(w = 5\) kN/m
Charges concentrées : \(P_1 = 10\) kN (à 2 m du support gauche) et \(P_2 = 15\) kN (à 4 m du support gauche)

1.1. Calcul de la charge totale appliquée :

Charge répartie totale :

\[ W_{\text{UR}} = w \times L \] \[ W_{\text{UR}} = 5\,\text{kN/m} \times 6\,\text{m} \] \[ W_{\text{UR}} = 30\,\text{kN} \]

Charges ponctuelles :

\[ P_{\text{tot}} = P_1 + P_2 \] \[ P_{\text{tot}} = 10 + 15 \] \[ P_{\text{tot}} = 25\,\text{kN} \]

Charge totale :

\[ P_{\text{total}} = 30 + 25 \] \[ P_{\text{total}} = 55\,\text{kN} \]

1.2. Équilibre vertical :

Soit \(R_a\) et \(R_b\) les réactions aux appuis gauche et droit respectivement,

\[ R_a + R_b = 55\,\text{kN} \]

1.3. Équilibre des moments (par rapport au support gauche A) :

La charge répartie de 30 kN agit en son centre de gravité, soit à 3 m de A.
Le moment dû à la charge répartie :

\[ M_{w} = 30\,\text{kN} \times 3\,\text{m} \] \[ M_{w} = 90\,\text{kN·m} \]

Moment de \(P_1\) :

\[ M_{P1} = 10\,\text{kN} \times 2\,\text{m} \] \[ M_{P1} = 20\,\text{kN·m} \]

Moment de \(P_2\) :

\[ M_{P2} = 15\,\text{kN} \times 4\,\text{m} \] \[ M_{P2} = 60\,\text{kN·m} \]

Moment total dû aux charges :

\[ M_{\text{total}} = 90 + 20 + 60 \] \[ M_{\text{total}} = 170\,\text{kN·m} \]

Équation du moment au support gauche A :

\[ R_b \times L = 170\,\text{kN·m} \]

D’où

\[ R_b = \frac{170}{6} \approx 28,33\,\text{kN} \]

1.4. Détermination de \(R_a\) :

\[ R_a = 55 – 28,33 \] \[ R_a \approx 26,67\,\text{kN} \]

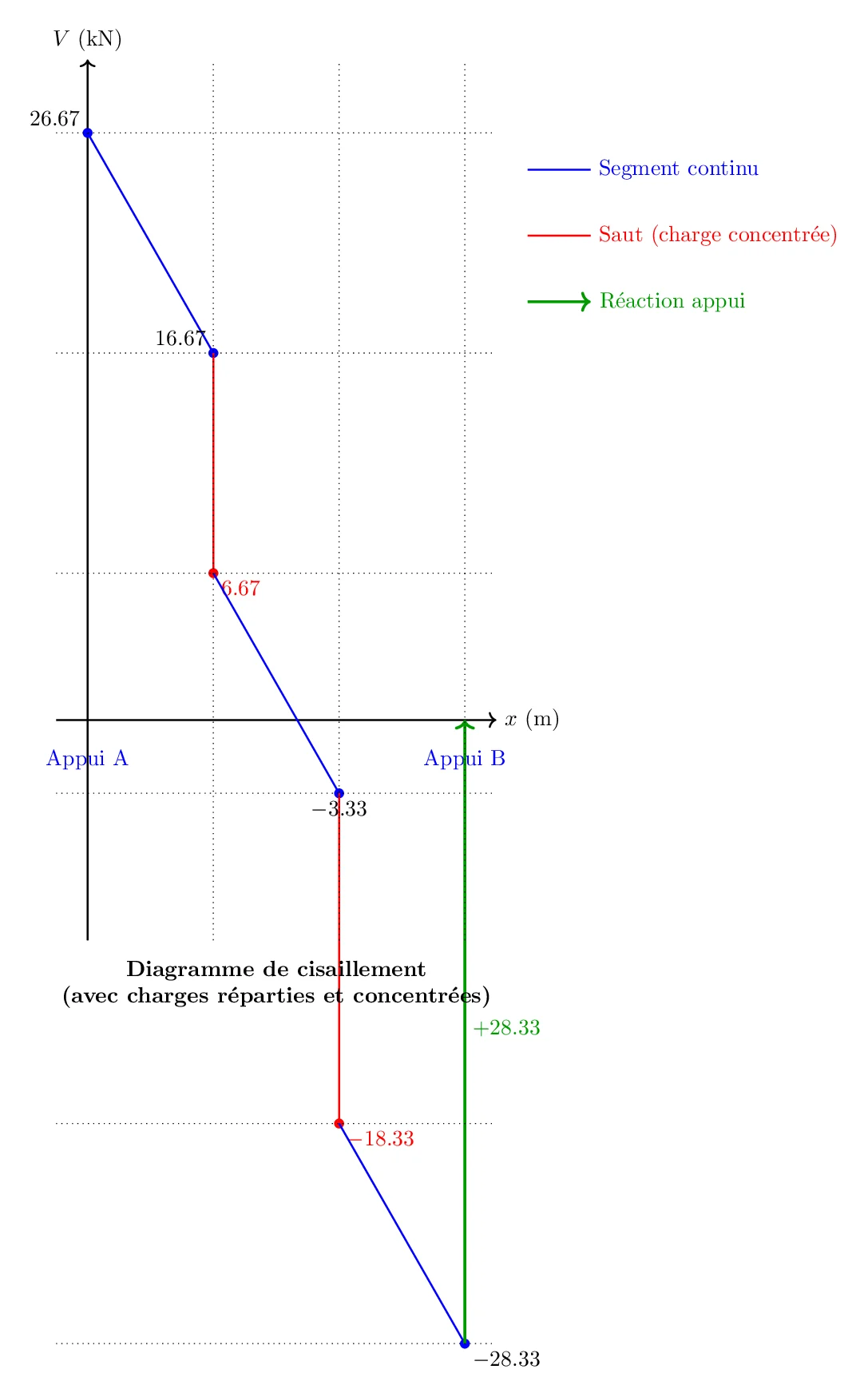
2. Construction du Diagramme de Cisaillement

Le diagramme de cisaillement s’établit en considérant les contributions des charges réparties et concentrées le long de la poutre.

2.1. À l’appui gauche \((x = 0)\) :

\[ V(0^+) = R_a = 26,67\,\text{kN} \]

2.2. Pour \(0 < x < 2\) m (avant \(P_1\)) :

La charge répartie diminue le cisaillement linéairement :

\[ V(x) = 26,67 – 5x \quad (\text{en kN}) \]

Juste avant \(P_1\) (x = 2 m) :

\[ V(2^-) = 26,67 – 5 \times 2 \] \[ V(2^-) = 16,67\,\text{kN} \]

2.3. En passant la charge \(P_1\) (x = 2 m) :

Le cisaillement subit une chute de 10 kN :

\[ V(2^+) = 16,67 – 10 \] \[ V(2^+) = 6,67\,\text{kN} \]

2.4. Pour \(2\) m \(< x < 4\) m (avant \(P_2\)) :

Diminution linéaire due à la charge répartie :

\[ V(x) = 6,67 – 5 \times (x – 2) \]

Juste avant \(P_2\) (x = 4 m) :

\[ V(4^-) = 6,67 – 5 \times 2 \] \[ V(4^-) = -3,33\,\text{kN} \]

2.5. En passant la charge \(P_2\) (x = 4 m) :

Chute de 15 kN :

\[ V(4^+) = -3,33 – 15 \] \[ V(4^+) = -18,33\,\text{kN} \]

2.6. Pour \(4\) m \(< x < 6\) m :

Continuité avec la charge répartie :

\[ V(x) = -18,33 – 5 \times (x – 4) \]

À l’appui droit (x = 6 m) :

\[ V(6^-) = -18,33 – 5 \times 2 \] \[ V(6^-) = -28,33\,\text{kN} \]

L’appui droit apporte une réaction de 28,33 kN (vers le haut) pour annuler le cisaillement.

Observation :
Le cisaillement maximum en valeur absolue est atteint à l’appui droit avec

\[ |V| = 28,33\,\text{kN} \]

3. Calcul de la Contrainte de Cisaillement Maximale

Données géométriques de la section :

Largeur de la section : \(b = 150\) mm
Hauteur de la section : \(h = 300\) mm
La poutre est en acier.

Moment d’inertie (\(I\)) de la section rectangulaire :

\[ I = \frac{b \, h^3}{12} = \frac{150 \times 300^3}{12} \] \[ I = \frac{150 \times 27\,000\,000}{12} \] \[ I = \frac{4\,050\,000\,000}{12} \] \[ I \approx 337\,500\,000\,\text{mm}^4 \]

Calcul du premier moment d’aire (\(Q\)) :

Pour un rectangle, la contrainte de cisaillement maximale se trouve à l’axe neutre (milieu en hauteur). Le premier moment d’aire pour la partie supérieure (ou inférieure) est :